Методика построения векторных диаграмм

Рис.5

А б

Рис.3 Рис.4

На схемах обмотки (или фазы) источника питания обозначают так, как показано на рис.2.

За условно положительное направление ЭДС в каждой фазе принимают направление от конца к началу.

Трехфазная симметричная система ЭДС может изображаться графиками, тригонометрическими функциями, векторами и функциями комплексного переменного. Графики изменения ЭДС симметричной системы показаны на рис.3. Если начальную фазу ЭДС фазы АХ принять равной нулю, то тригонометрическая форма представления трехфазной симметричной системы ЭДС (прямой последовательности) имеет вид е_А = Е_m sin wt; е_В= Е_m sin (wt – 2 p/ 3)

е_С = Е_m sin (wt – 4 p/ 3) = Е_m sin (wt + 2 p/ 3).

Комплексная форма записи:

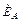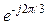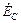= Е; = Е 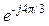; = Е = Е ,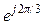

где 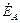, , 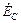- комплексы действующих значений ЭДС;

Е – действующее значение ЭДС: Е = .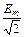

Для такой системы справедливы соотношения:

е_А + е_В + е_С 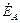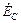= 0;

+ + = 0.

Векторная диаграмма трехфазной симметричной системы ЭДС показана на рис.4: а – прямая последовательность фаз; б – обратная последовательность фаз. Последовательность фаз определяет направление вращения трехфазных двигателей, ее нужно учитывать также при включении трехфазных генераторов на параллельную работу. Для определения последовательности фаз служат фазоуказатели.

Обмотки фаз генератора обычно соединяют звездой, то есть концы обмоток X, Y, Z соединяют в общую точку N, называемую нулевой или нейтральной (рис.5). При этом от трехфазного генератора отходят 4 провода – три линейных А, В, С и нейтральный N – n. В трехфазных четырехпроводных сетях нейтральный провод заземляют.

Однофазные приемники также могут соединяться звездой, то есть их концы x, y, z соединяют в общую точку n и присоединяют к нейтральному проводу, а к свободным началам фаз а, в, с подводят энергию по линейным проводам от трехфазного генератора.

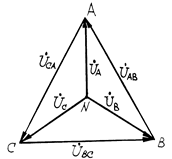
Рис.6

Напряжения U_A, U_B, U_C между линейными и нейтральными проводами, то есть между началом и концом фазы, называются фазными. Напряжения между соответствующими линейными проводами U_AB, U_BC, U_CA, то есть между началами фаз, называются линейными. Эти напряжения связаны между собой соотношениями:

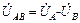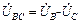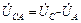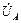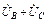; ; ; + = 0; + = 0.

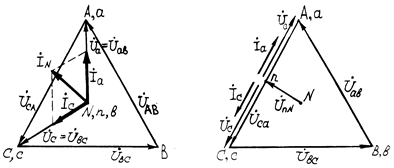
На рис.6 показана векторная диаграмма линейных и фазных напряжений генератора. Из диаграммы видно, что для симметричной системы напряжений между фазными и линейными напряжениями существует зависимость

U_л = 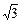U_ф» 1,73 U_ф.

Токи I_A, I_B, I_C, протекающие в линейных проводах, называются линейными. Токи, протекающие в обмотках генератора или фазах приемника, называются фазными. При соединении звездой фазные и линейные токи равны:

I_л = I_ф.

Применяя к узлу n (рис.5) первый закон Кирхгофа, получаем ток в нулевом проводе:

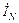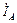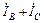= + . (1)

Приемники называются симметричными, если комплексные сопротивления их фаз Z _a = Z_a 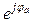; Z _в = Z_в 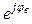; Z _с = Z_с 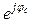равны между собой, то есть равны полные сопротивления отдельных фаз:

Z_a= Z_в = Z_с= Z_ф (2)

и одинаковы углы сдвига фаз:

j_а = j_в = j_с = j_{ф .} (3)

Если одно из условий симметрии, характеризующее равномерность (2) или неоднородность (3) нагрузки, не выполняется, приемники называются несимметричными.

Сдвиг по фазе между током и напряжением j_ф = y_u – y_i на приемнике зависит от вида нагрузки (табл. 1) и определяется из треугольника сопротивлений фазы нагрузки. Например, для фазы с активно-индуктивной нагрузкой комплексное сопротивление равно:

Z _ф = R + jX = Z_ф ,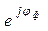

где Z_ф = 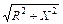- полное сопротивление фазы;

j_ф = arctg 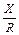- угол сдвига между током и (4). напряжением

Таблица 1

Вид нагрузки	Схема замещения	Векторная диаграмма
Активная
Индуктивная
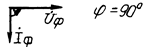
Емкостная
Активно-индуктивная

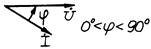
Применяя для трехфазной цепи, соединенной звездой (рис.5), метод двух узлов, получаем 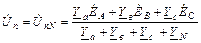, (5)

где

; ; ; -

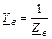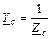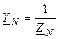комплексные проводимости фаз нагрузки с учетом сопротивления линейных проводов и нейтрального провода, если сопротивлением проводов нельзя пренебречь.

При симметричной нагрузке Y _a = Y _в = Y _с = Y _ф, а

ток в каждой фазе приемника I_ф = 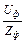одинаков, ток в нейтральном проводе 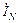= 0. Это позволяет выполнить трехфазную линию трехпроводной.

Векторная диаграмма для напряжений и токов при активно-индуктивной симметричной нагрузке показана на рис.7.

Рис.7 Рис.8

Если сопротивлением проводов можно пренебречь, то Z _N = 0, Y _N = ¥. При этом напряжение между нейтралями генератора и нагрузки = 0. Фазные напряжения нагрузки равны соответствующим напряжениям генератора, т.е. остаются симметричными при любой несимметричной нагрузке (например, неравномерной активной, рис.8):

= ; ; ; = .

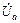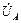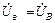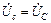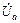Ток в нейтральном проводе равен: = + .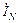

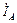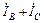Отсутствие нейтрального провода, т.е. Z _N = ¥, Y _N = 0 значительно нарушает симметрию фазных напряжений нагрузки, появляется смещение между нейтралями генератора и нагрузки 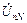(рис.9).

Комплексные значения напряжений на нагрузке можно определить по соотношениям:

= - ;

- ;

- .

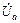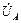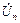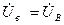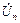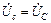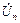Фазные токи равны линейным:

= = ; = ; = ;

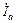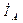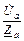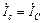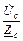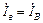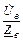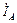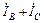+ = 0.

Понятие мощности, потребляемой каждой из фаз приемника, дано в лабораторной работе №1 (п.4).

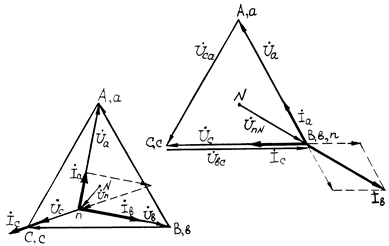
Рис.9 Рис.10

При построении векторных диаграмм необходимо выбрать удобный масштаб напряжений m_U 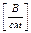и токов m_I . Векторная диаграмма напряжений нагрузки строится совмещенной с векторной диаграммой напряжений генератора. Линейные и фазные напряжения генератора постоянны, следовательно, линейные напряжения нагрузки также постоянны и равны линейным напряжениям генератора, если падением напряжения на проводах можно пренебречь:

= ; ; .

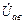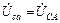Исключения составляют случаи обрыва линейных проводов.

Так как = = 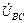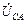, то имеем равносторонний треугольник линейных напряжений генератора. Нейтральная точка генератора N всегда находится в центре тяжести треугольника; фазные напряжения 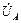, , 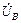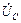сдвинуты относительно друг друга на 120°.

Таким образом, с помощью циркуля строят засечками равносторонний треугольник линейных напряжений генератора и находят с помощью засечек точку N генератора (рис.6).

При наличии нейтрального провода с нулевым сопротивлением (Z _N =0) при любой нагрузке 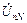= 0, то есть потенциалы нейтральных точек нагрузки n и генератора N совпадают (рис.7,8). При отсутствии нейтрального провода и несимметричной нагрузки появляется напряжение между нейтралями 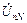. В этих случаях из точек А, В, С проводят дуги радиусами U_а, U_в, U_c. Общая точка пересечения дуг (точка n на рис.9) определяет потенциал нейтральной точки нагрузки n относительно точки N генератора.

Векторную диаграмму токов нагрузки строят совмещенной с векторной диаграммой напряжений нагрузки. Для каждой фазы приемника определяют угол сдвига фаз j_ф = y_u – y_i между напряжением и током по (4) в зависимости от вида нагрузки (табл. 1).

Откладывая на диаграмме фазных напряжений приемника под соответствующими углами фазные токи, получаем векторную диаграмму токов. Ток в нейтральном проводе определяем графически суммированием токов: I_N = 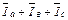(рис.8). При отсутствии нейтрального провода векторная сумма фазных токов, сходящихся в узле n, равна нулю: 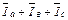= 0 (рис.9).

Представляют интерес некоторые режимы работы приемников трехфазной цепи.

При коротком замыкании приемников одной из фаз, например фазы В (рис.10) в трехпроводной цепи, напряжение 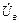= 0, потенциал точки n совпадает с потенциалом точки в (В). В результате напряжения других фаз нагрузки возрастают до линейных напряжений генератора, т. е. в 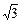раз, соответственно возрастают и токи в них. В короткозамкнутой фазе ток резко возрастает и определяется по первому закону Кирхгофа:

.

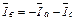При обрыве одного из проводов, например В-в в четырехпроводной цепи, приемники данной фазы остаются без энергии: 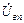= 0 (рис.11). Режим работы двух других фаз не нарушается. Линейные напряжения между оборванными и другими проводами (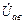, 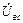) уменьшаются до фазных.

Отключение одной из фаз в четырехпроводной цепи также не влияет на режим работы других приемников. Ток в нейтральном проводе определяется только двумя фазными токами. При отключении одной из фаз, например фазы В, и отсутствии нейтрального провода приемники двух других фаз оказываются включенными последовательно на линейное напряжение источника. Ток в фазах a-x, c-z один и тот же. Фазные напряжения на них пропорциональны их полным сопротивлениям. Система из трехфазной превращается в однофазную. Диаграмма напряжений и токов при активной R_a = R_c нагрузке фаз дана на рис.12.

Дата добавления: 2015-05-06