
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Синтез комбинационной схемы в заданном базисе логических элементов
|
|
|
|
При разработке схем логических устройств, приведенных на рисунках 5.21, 5.22, 5.23 и 5.24 использован функционально полный набор логических элементов, включающий элементы И, ИЛИ и НЕ. На практике, например с целью сокращения номенклатуры используемых логических элементов, часто ставится задача выполнить синтез логического устройства, используя только логические элементы И-НЕ или ИЛИ-НЕ. Ранее было показано, что каждый из этих элементов отдельно взятый представляет собой функционально полный набор логических элементов. Особый интерес представляет логический элемент штрих Шеффера. Это, в первую очередь, обусловлено тем, что промышленностью серийно выпускаются такие логические элементы с разным числом входов, в частности, двух-, трех-, четырех- и восьмивходовые. При большом числе логических элементов в схеме применение однотипных элементов позволяет уменьшить общее число корпусов интегральных микросхем, что, в свою очередь, обеспечивает более качественное решение задачи инженерного проектирования.
Для построения логического устройства на заданных логических элементах необходимо полученную в процессе минимизации логическую функцию преобразовать таким образом, чтобы в нее входили только логические операции, реализуемые заданными логическими элементами.
Пусть, например, требуется разработать схему логического устройства, реализующего рассматриваемую ранее логическую функцию, только на двухвходовых элементах И-НЕ. Чтобы перейти к базису И-НЕ, необходимо преобразовать ранее полученную тупиковую форму логической функции, используя закон двойного отрицания и правила де Моргана. При этом не важно, какая форма логического выражения – ДНФ или КНФ – используется.
|
|
|
Преобразуем выражения (5.3) и (5.4) к базису логических элементов 2И-НЕ:
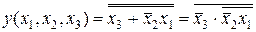 . (5.9)
. (5.9)
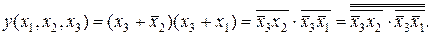 (5.10)
(5.10)
Функциональная схема логического устройства, синтезированного на основе выражения (5.9), представлена на рисунке 5.25, а устройства, синтезированного на основе выражения (5.10) – на рисунке 5.26.
Как видно из сравнения рисунков 5.23 и 5.25, а также 5.24 и 5.26, при переходе к базису однотипных логических элементов количество элементов в схеме может и увеличиться, но при учете использованных корпусов интегральных микросхем, как правило, имеет место выигрыш. Например, чтобы реализовать схему на рисунке 5.23, потребуется 3 корпуса ИМС, в то время как для реализации схемы на рисунке 5.25 нужен всего один корпус ИМС. Аналогично для реализации схемы на рисунке 5.24 нужно 3 корпуса ИМС, а схемы на рисунке 5.26 – 2 корпуса.

Рисунок 5.25 – Комбинационная схема, реализующая функцию (5.3)
в базисе элементов 2И-НЕ

Рисунок 5.26 – Комбинационная схема, реализующая функцию (5.4)
в базисе элементов 2И-НЕ
|
|
|
|
|
Дата добавления: 2015-05-06; Просмотров: 826; Нарушение авторских прав?; Мы поможем в написании вашей работы!