Непрерывное наращение и дисконтирование — непрерывные проценты

Сравнение интенсивности процессов наращения и дисконтирования по разным видам процентных ставок

Выше для наращения и дисконтирования использовались ставки i_s, i, j, d_s, d, f. Естественно, что даже в одинаковых исходных условиях применение этих ставок приводит к различным результатам. В связи с этим представляет определенный практический интерес сравнение результатов наращения и дисконтирования по различным ставкам. Для этого достаточно сопоставить множители наращения, полученные по разным ставкам, аналогично нужно поступить и с дисконтными множителями. Частично эта проблема рассматривалась при сравнении процессов наращения по простой и сложной ставке процентов (см. параграф 2.2).

Опустив формальные доказательства, сразу запишем необходимые соотношения при условии, что абсолютные размеры ставок одинаковы. Варианты со ставками j и f рассматривать не будем, так как результат зависит и от значения т.

Множители наращения соотносятся следующим образом:

при 0 < п < 1 (1 + i) ⁿ < (1 + ni_s) < 1/(1 - nd_s) < 1/(1 - d) ⁿ;

при n =1 (1 + i) = (1 + i_s) < 1/(1 - d_s) = 1/(1 - d);

при п > 1 (1 +ni_s) < (1 + i) ⁿ < 1/(1 - d) ⁿ < 1/(1 - nd_s).

В табл. 2.3 приведены значения множителей наращения для разных видов ставок при условии, что размер ставок одинаков и равен 20%.

Таблица 2.3 Множители наращения для разных видов ставок (20%)

Срок	Множители наращения
is	i	ds	d
0,2	1,04	1,0371	1,0417	1,0456
0,5	1,10	1,0954	1,1111	1,1180
0,8	1,16	1,1570	1,1905	1,1954
1,0	1,20	1,200	1,2500	1,2500
1,5	1,30	1,3145	1,4286	1,3975
2,0	1,40	1,4400	1,6667	1,5625
3,0	1,60	1,7280	2,5000	1,9531
5,0	2,00	2,4883	∞	3,0517
10,0	11,00	6,1917	∞	9,3132

Аналогичным образом получим систему неравенств для дисконтных множителей:

при 0< n <1 (1 - d) ⁿ < (1 - nd_s) < 1/(1 + ni_s) < 1/(1 + i) ⁿ,

при n = 1 (1 - d) = (1 - d_s) < 1/(1 + i_s) = 1/(1 + i),

при n > 1 (1 - nd_s) < (1 - d) ⁿ < 1/(1 + i) ⁿ < 1/(1 + ni_s).

В практических финансово-кредитных операциях непрерывное наращение, т.е. наращение за бесконечно малые отрезки времени, применяется крайне редко. Существенно большее значение непрерывное наращение имеет в анализе сложных финансовых проблем, например при обосновании и выборе инвестиционных решений, в финансовом проектировании. Немаловажное значение имеет и то, что с помощью непрерывных процентов удается учесть сложные закономерности процесса наращения, например использовать изменяющиеся по определенному закону процентные ставки.

При непрерывном наращении процентов применяют особый вид процентной ставки — силу роста (force of interest). Сила роста характеризует относительный прирост наращенной суммы за бесконечно малый промежуток времени. Она может быть постоянной или изменяться во времени.

Постоянная сила роста. Напомним, что при дискретном начислении процентов т раз в году по номинальной ставке j наращенная сумма находится как

S = Р (1 +j/m)^mn.

Чем больше т, тем меньше промежуток между моментами начисления процентов. В пределе при т, стремящемся к бесконечности, имеем

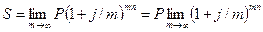
Известно, что 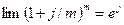, где е — основание натуральных логарифмов.

Наращенная сумма находится как

.

Для того чтобы отличить непрерывную ставку от дискретной, силу роста обычно обозначают как δ. Теперь окончательно запишем

(2.18)

Итак, при непрерывном наращении процентов наращенная сумма равна конечной величине, зависящей от первоначальной суммы, срока наращения и силы роста. Последняя представляет собой номинальную ставку сложных процентов при m → ∞.

Дискретные и непрерывные ставки наращения находятся в функциональной зависимости между собой. Из равенства множителей наращения 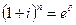следует

(2.19) (2.20)

Пример 2.12. Сумма, на которую начисляются проценты, равна 2 млн. руб., сила роста — 10%, срок — пять лет. Наращенная сумма составит

S = 2 000 000 х е^{0,1 x 5} = 3 297 744,25 руб.

Непрерывное наращение по ставке δ = 10% равнозначно (см. формулу (2.20)) наращению за тот же срок сложных годовых процентов по ставке

i = e ^0,1 - 1 = 0,1051709, или 10,51709%.

В самом деле, мы получим ту же наращенную сумму, применив эту ставку.

S = 2 000 000(1 + 0,1051709)⁵ = 3 297 744,25 руб.

Дисконтный множитель на основе силы роста находится элементарно. Для этого решим уравнение (2.18) относительно Р.

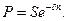
Дисконтный множитель, следовательно, равен

Переменная сила роста. Пусть сила роста изменяется во времени, следуя определенному закону — непрерывной функции времени: , тогда наращенная сумма и современная стоимость определяются как

Рассмотрим варианты определения множителя наращения для случаев, когда величина δ _t представляет собой линейную и экспоненциальную функцию. Если это линейная функция δ _t = δ₀ + at, где δ₀ — начальное значение силы роста, а — ее прирост, то

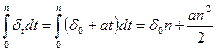
Множитель наращения находится как

(2.21)

Пример 2.13. Пусть начальное значение силы роста равно 8%, ставка непрерывно и линейно изменяется, прирост за год 2% (а = 0,02). Срок наращения — пять лет. Для расчета множителя наращения за весь срок найдем его степень:

Искомый множитель составит е ^0,65 = 1,91554. Продолжим пример. Предположим, что сила роста теперь линейно уменьшается: а = -0,02. В этом случае степень множителя наращения равна 0,15, соответственно е ^0,15 = 1,16183.

Рассмотрим ситуацию, когда сила роста изменяется по геометрической прогрессии: δ _t = δ₀ a_t; δ₀ — начальное значение силы роста, а — постоянный темп роста. В этом случае степень множителя равна

,

а сам множитель находится как

. (2.22)

Пример 2.14. Начальный уровень силы роста 8%, процентная ставка непрерывно увеличивается (годовой прирост 20%, т.е. а = 1,2), срок — пять лет. Степень множителя наращения за весь срок равна

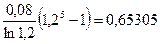, соответственно е ^0,65305 = 1,9214.

Дата добавления: 2015-03-31