Сформулируйте теорему о приведении квадратичной формы к главным осям

Покажите, что собственные векторы, отвечающие различным собственным значениям симметрической матрицы, ортогональны.

Пусть матрица A - симметричная матрица (A = AT), имеющая собственные значения λ1,..., λn. И пусть v1,..., vn - собственные вектора, отвечающие указанным собственным значениям: Avi = λivi, ∀i = 1..n. Рассмотрим скалярное произведение ∀i, j:

λj(vi, vj) = (vi, λjvj) = (vi, Avj) = (AT vi, vj) = (Avi, vj) = (λivi, vj) = λi(vi, vj)

Мы получили λj(vi, vj) = λi(vi, vj), значит:

(λj − λi) · (vi, vj) = 0

Так как λj = λi, получаем исходное утверждение: (vi, vj) = 0, ∀i, j = 1..n, i = j, что подтверждает ортогональность собственных векторов.

Канонический вид квадратичной формы в ортонормированном базисе называют каноническим видом в главных осях.

Теорема: Ортонормированный базис пространства Rn, состоящий из собственных векторов симметрической матрицы, является каноническим базисом квадратичной формы

F = xTAx.

68. Приведите форму к нормальному виду методом Лагранжа.

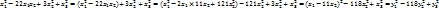
где ; ;

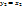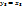
69. Сформулируйте закон инерции квадратичных форм. Можно ли квадратичную форму 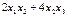с помощью невырожденного линейного преобразования переменных привести к виду ? Ответ обоснуйте.

Закон инерции квадратичных форм: Число слагаемых с положительными (отрицательными) коэффициентами в каноническом виде квадратичной формы не зависит от способа приведения квадратичной формы к аноническому виду.

Приведем кв. ф. f(x1, x2, x3) к канон. виду:

f = 2x1x2 + 4x2x3 = (x21+ x22+ 4x23+ 2x1x2 + 4x2x3 + 4x1x3) − (x21+ 4x1x3 + 4x23) − x22= (x1 + x2 + 2x3)2 − (x1 + x3)2 − x22

В каноническом виде мы получили 2 ’-’ (c отрицательным знаком) и 1 - ’+’ (с положительным знаком). По закону инерции кв. ф. нельзя привести кв. ф. f(x1, x2, x3) к каноническому вид y21 − 2y22 + y23 с 2мя положительными слагаемыми и одним отрицательным слагаемым.

70.

Дата добавления: 2015-03-31