Приклад. Дано еліпс, розміщений у площині

Дано еліпс, розміщений у площині 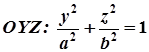. Записати рівняння поверхні обертання, утвореної при обертанні цього еліпса навколо осі .

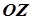Розв’язання

За формулою (3) рівняння цієї поверхні обертання має вигляд:

.

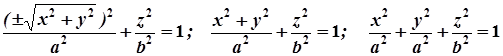Ця поверхня називається еліпсоїдом обертання.

§ 4. Циліндричні поверхні

Означення 4.1. Поверхня, утворена внаслідок руху прямої, яка перетинає задану криву і залишається паралельною даній прямій, називається циліндричною поверхнею.

Прямі, які повністю лежать на цій поверхні і паралельні

заданій прямій, називаються твірними циліндричної поверхні, а крива L, яку перетинають ці твірні, називається напрямною цієї поверхні (рис. 7.7).

Припустимо, що напрямна крива циліндричної поверхні розміщена в деякій площині, а твірні циліндричної поверхні перпендикулярні до цієї площини. Введемо прямокутну систему координат так, щоб напрямна крива L містилась у площині , а твірні були паралельні до осі 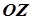(рис. 7.8).

Припустимо, що крива L у плоскій системі координат задана рівнянням

(1)

Нехай 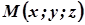– довільна точка циліндричної поверхні, тоді її проекція на площину 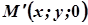лежить на кривій L. Тому . Отже, координати довільної точки М циліндричної поверхні задовольняють рівняння (1).

Якщо ж деяка точка 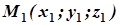не лежить на даній циліндричній поверхні, то її проекція на площину не лежать на кривій L і, отже, .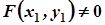

Таким чином, рівняння (1) задовольняють координати довільної точки циліндричної поверхні і тільки вони, тому це рівняння буде рівнянням даної циліндричної поверхні.

Аналогічно встановлюємо, що коли напрямна крива задана рівнянням у площині 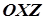, то в просторовій системі координат це рівняння задає циліндричну поверхню, твірні якої паралельні до осі .

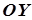Якщо ж крива задана рівнянням 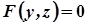у площині 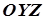, то в просторовій системі координат це рівняння буде рівнянням циліндричної поверхні, твірні якої паралельні до осі .

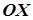В результаті приходимо до такого висновку: якщо в рівнянні поверхні відсутня одна із змінних, то ця поверхня є циліндром, твірні якого паралельні до тієї координатної осі, змінна якої відсутня в даному рівнянні.

Приклади

1) Еліптичний циліндр (рис. 7.9).

Його рівняння

.

Напрямною є еліпс з півосями і .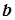

2) Гіперболічний циліндр (рис. 7.10).

Рівняння

.

Напрямною є гіпербола з дійсною піввіссю .

3) Параболічний циліндр (рис. 7.11).

Його рівняння

.

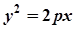Напрямною є парабола.

На прикладі покажемо, яким чином можна знаходити рівняння циліндричної поверхні, твірні якої мають довільний напрям.

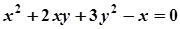Задача. Скласти рівняння циліндричної поверхні, напрямна якої лежить в площині і має рівняння , а твірні паралельні вектору .

Розв’язання

Рівняння напрямної у просторі матиме вигляд:

(2)

Нехай 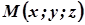– довільна точка циліндричної поверхні. Проведемо через неї твірну 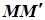, де 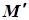– точка перетину цієї твірної з площиною , а отже, – і з напрямною (рис. 7.12). Нехай координрати точки 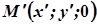. Оскільки , то її координати задовольняють рівняння (2), тому

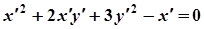. (3)

Запишемо параметричні рівняння твірної 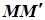, заданої точкою 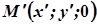і напрямним вектором .

(4)

Змінні 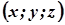в цьому рівнянні є координатами точок твірної, а отже, й координатами точок циліндричної поверхні. Координати точки 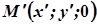задовольняють рівняння (3) і (4). Тому, виключаючи з рівнянь (3) і (4), дістаємо співвідношення між координатами точок циліндра, тобто рівняння циліндра. Маємо:

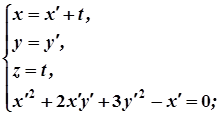
Отже, рівняння даної циліндричної поверхні:

.

§ 5. Конічні поверхні

Дата добавления: 2015-03-31