
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Парная регрессия
|
|
|
|
Пусть нас интересует установление взаимосвязи между двумя количественными признаками  и
и  .
.
 и
и  могут быть независимы, связаны между собой функциональной либо корреляционной зависимостью.
могут быть независимы, связаны между собой функциональной либо корреляционной зависимостью.
При корреляционной зависимости изменение каждого отдельного значения  необязательно влечет за собой изменение значения
необязательно влечет за собой изменение значения  , однако изменение
, однако изменение 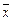 приводит к изменению
приводит к изменению 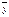 .
.
Регрессионный анализ оценивает вид функции зависимости между  и
и 
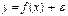 ,
,  - ошибка оценки. Чтобы установить вид зависимости строится поле корреляции. На плоскости наносятся точки с координатами
- ошибка оценки. Чтобы установить вид зависимости строится поле корреляции. На плоскости наносятся точки с координатами 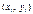 ,
,  , и по расположению точек делаются выводы о виде зависимости.
, и по расположению точек делаются выводы о виде зависимости.
Пусть вид зависимости линейный 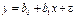 Коэффициенты
Коэффициенты  и
и  найдем по методу наименьших квадратов. Составим функцию
найдем по методу наименьших квадратов. Составим функцию

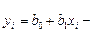 теоретические значения y.
теоретические значения y.
Найдем  и
и  такие, при которых функция S достигает минимума.
такие, при которых функция S достигает минимума.

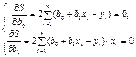

Перейдем к средним значениям, поделив эти уравнения на n.
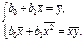
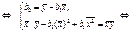

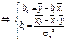
Уравнение вида  называется уравнением линии регрессии У на Х. Угловой коэффициент прямой называется коэффициентом регрессии.
называется уравнением линии регрессии У на Х. Угловой коэффициент прямой называется коэффициентом регрессии.
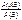 , P(B)>0 Аналогично, условной вероятностью события B при условии, что событие A уже произошло называется:
P(B/A)=
, P(B)>0 Аналогично, условной вероятностью события B при условии, что событие A уже произошло называется:
P(B/A)=  , P(A)>0
Из формул следует теорема умножения:
P(AB)=
, P(A)>0
Из формул следует теорема умножения:
P(AB)= 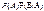 =
=  Вероятность произведения двух произвольных событий равна произведению вероятности одного из событий на условную вероятность второго, при условии, что первое уже произошло.
Распространим теорему умножения на конечное число событий
P(A1 A2 Ak)=P(A1)P(A2/A1)*…*P(Ak/A1A2 …Ak-1)
Определение 2 События А и В называются независимыми, если вероятность произведения равна произведению вероятности этих событий.
P(AB)=P(A)P(B)
для независимых событий условные и безусловные вероятности совпадают.
P(A/B)=P(A)Для конечного числа независимых событий вероятность произведения равна произведению вероятностей.
P(A1A2…Ak)=P(A1)P(A2)…P(AK)
9. Функция распределения вероятности и ее свойства.
Функцией распределения сл\в Х наз-ся ф-я F(x), выражающая для каждого х вер-ть т\ч сл\в Х примет значение, меньшее х.
Вероятность произведения двух произвольных событий равна произведению вероятности одного из событий на условную вероятность второго, при условии, что первое уже произошло.
Распространим теорему умножения на конечное число событий
P(A1 A2 Ak)=P(A1)P(A2/A1)*…*P(Ak/A1A2 …Ak-1)
Определение 2 События А и В называются независимыми, если вероятность произведения равна произведению вероятности этих событий.
P(AB)=P(A)P(B)
для независимых событий условные и безусловные вероятности совпадают.
P(A/B)=P(A)Для конечного числа независимых событий вероятность произведения равна произведению вероятностей.
P(A1A2…Ak)=P(A1)P(A2)…P(AK)
9. Функция распределения вероятности и ее свойства.
Функцией распределения сл\в Х наз-ся ф-я F(x), выражающая для каждого х вер-ть т\ч сл\в Х примет значение, меньшее х.  Дискретнойназывается случайная величина, которая принимает конечное или счетное множество значений.
Пусть xi – возможное значение случайной величины
Дискретнойназывается случайная величина, которая принимает конечное или счетное множество значений.
Пусть xi – возможное значение случайной величины 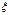 .
.
 - вероятность этих значений.
Множество пар (xi, pi) называются законом распределения вероятностей дискретной случайной величины.
Обычно закон распределения изображается в виде таблиц
Для полной вероятностной характеристики случайной дискретной величины необходимо знать ее закон распределения.
Определение:Непрерывной называется случайная величина, которая может принимать значения из некоторых промежутков.
Свойства функции распределения
1) ФР сл\в есть неотрицательная ф-я, заключенная м\у 0 и 1:
- вероятность этих значений.
Множество пар (xi, pi) называются законом распределения вероятностей дискретной случайной величины.
Обычно закон распределения изображается в виде таблиц
Для полной вероятностной характеристики случайной дискретной величины необходимо знать ее закон распределения.
Определение:Непрерывной называется случайная величина, которая может принимать значения из некоторых промежутков.
Свойства функции распределения
1) ФР сл\в есть неотрицательная ф-я, заключенная м\у 0 и 1: 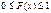 2) ФР сл\в есть неубывающая ф-я на всей числовой оси.
2) ФР сл\в есть неубывающая ф-я на всей числовой оси.  при
при 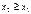 3) На минус бесконечности ФР = нулю, на плюс бесконечности ФР = единице.
3) На минус бесконечности ФР = нулю, на плюс бесконечности ФР = единице.
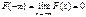 ;
;  4) Вер-ть попадания сл\в в интервал
4) Вер-ть попадания сл\в в интервал 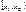 (включая
(включая 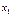 ) равна приращению её ФР на этом интервале, т.е.
) равна приращению её ФР на этом интервале, т.е.  16. Равномерное распределение.
Плотность распределения:
16. Равномерное распределение.
Плотность распределения:

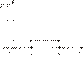 Рисунок 1 График плотности вероятности равномерного распределения
Функция распределения:
Рисунок 1 График плотности вероятности равномерного распределения
Функция распределения:
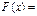

 Рисунок 2 График функции равномерного распределения
Равномерное распределение имеет два параметра
Рисунок 2 График функции равномерного распределения
Равномерное распределение имеет два параметра  и
и  .
Матожидание и дисперсия:
.
Матожидание и дисперсия:
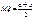 ,
,  . Показательное распределение.
Показательным, называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью
. Показательное распределение.
Показательным, называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью
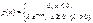 Показательное распределение имеет один параметр
Показательное распределение имеет один параметр 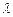 .
.
 Рисунок 3 График плотности вероятности показательного распределения
Функция распределения:
Рисунок 3 График плотности вероятности показательного распределения
Функция распределения:

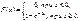
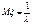 ,
, 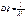 ,
, 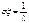 .
Характерным свойством показательного распределения является равенство матожидания и среднеквадратического отклонения:
.
Характерным свойством показательного распределения является равенство матожидания и среднеквадратического отклонения: 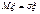 .
21. Условный закон распределения.
Условным законом распределения случайной величиныx, входящий в систему (
.
21. Условный закон распределения.
Условным законом распределения случайной величиныx, входящий в систему ( называется ее закон распределения, вычисленный при условии, что
называется ее закон распределения, вычисленный при условии, что  принимает значение у.
Пусть (
принимает значение у.
Пусть ( - непрерывный вектор с плотностью вероятности p(x,y).
Пусть B=(y<
- непрерывный вектор с плотностью вероятности p(x,y).
Пусть B=(y<  <
< 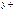 ∆y)
Тогда условная функция распределения случайной величины x при условии, что событие В произошло
∆y)
Тогда условная функция распределения случайной величины x при условии, что событие В произошло
 Пользуясь формулой умножения имеем
P=
Пользуясь формулой умножения имеем
P=  Функция
Функция  называется условной функцией распределения случайной величины x при условии В.
Возьмем производную от (1), устремив при этом ∆y к 0.
называется условной функцией распределения случайной величины x при условии В.
Возьмем производную от (1), устремив при этом ∆y к 0.
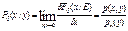 Функция
Функция  называется условной плотностью вероятности случайной величиныx при условии, что h равен у.
Из (2) следует аналогичная теорема умножения
называется условной плотностью вероятности случайной величиныx при условии, что h равен у.
Из (2) следует аналогичная теорема умножения
 Из можем получить непрерывный аналог формулы полной вероятности
Из можем получить непрерывный аналог формулы полной вероятности  Из можно получить условную функцию распределения случайной величины x при условии, что h равен у.
Из можно получить условную функцию распределения случайной величины x при условии, что h равен у.
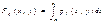 26. Эмпирическая функция распределения.
Также как и в теории вероятности для описания изучаемого признака вводится функция распределения. Пусть Х – изучаемый признак,
26. Эмпирическая функция распределения.
Также как и в теории вероятности для описания изучаемого признака вводится функция распределения. Пусть Х – изучаемый признак, 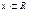 .Эмпирической функцией распределения называется функция, определяющая для каждого значения x относительную частоту события x<X
.Эмпирической функцией распределения называется функция, определяющая для каждого значения x относительную частоту события x<X
 nx-число вариант меньших x
n- объем выборки
nx /n – относительная частота события
В отличие от эмпирической функции распределения выборки функцию распределения F(x) генеральной совокупности называют теоретической ф-ей распределения.
Свойства:
1. для любого x функция распределения 0
nx-число вариант меньших x
n- объем выборки
nx /n – относительная частота события
В отличие от эмпирической функции распределения выборки функцию распределения F(x) генеральной совокупности называют теоретической ф-ей распределения.
Свойства:
1. для любого x функция распределения 0  2. F(x) –неубывающая функция.
3. Fn(x) непрерывна слева в каждой точке
2. F(x) –неубывающая функция.
3. Fn(x) непрерывна слева в каждой точке 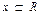 4. Если a=min{xi}, то для каждого x<=a Fn(x)=0
Если b=min{xi}, то для каждого x>b Fn(x)=1
На основе закона больших чисел можно показать, что при
4. Если a=min{xi}, то для каждого x<=a Fn(x)=0
Если b=min{xi}, то для каждого x>b Fn(x)=1
На основе закона больших чисел можно показать, что при  эмпирическая функция распределения стремится по вероятности к теоретической.
эмпирическая функция распределения стремится по вероятности к теоретической.
 Следовательно эмпирическая функция распределения служит для оценки вида теоретической ф-и распределения.
31. Доверительные интервалы.
Пусть вид распределения изучаемого признака Х известен
Следовательно эмпирическая функция распределения служит для оценки вида теоретической ф-и распределения.
31. Доверительные интервалы.
Пусть вид распределения изучаемого признака Х известен 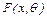 , но неизвестно значение входящего параметра
, но неизвестно значение входящего параметра 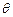 (тетра).
Определение 6.1. Оценка неизвестного параметра, которая задается двумя числами (концами интервала) называется интервальной.
Пусть по выборке получена точечная оценка
(тетра).
Определение 6.1. Оценка неизвестного параметра, которая задается двумя числами (концами интервала) называется интервальной.
Пусть по выборке получена точечная оценка 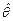 неизвестного параметра
неизвестного параметра 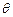 . Эта оценка тем точнее, чем меньше
. Эта оценка тем точнее, чем меньше 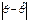 .
Пусть
.
Пусть  , где
, где  .
Методы математической статистики не позволяют на 100% утверждать, что выполняется это неравенство.
Можно лишь говорить о вероятности его выполнения
.
Методы математической статистики не позволяют на 100% утверждать, что выполняется это неравенство.
Можно лишь говорить о вероятности его выполнения
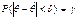 .
Величина
.
Величина 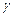 - называется доверительной вероятностью или надежностью. В качестве
- называется доверительной вероятностью или надежностью. В качестве 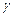 берут число близкое к единице: 0,95; 0,99; 0,995.
Оно выбирается исследователем самостоятельно. Раскрыв знак модуля получим определение доверительного интервала
берут число близкое к единице: 0,95; 0,99; 0,995.
Оно выбирается исследователем самостоятельно. Раскрыв знак модуля получим определение доверительного интервала
 .
Доверительным называется интервал
.
Доверительным называется интервал  , который покрывает неизвестный параметр
, который покрывает неизвестный параметр 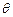 с заданной надежностью
с заданной надежностью 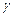 . При этом
. При этом  называется точностью оценки.
Замечание Неверно говорить, что
называется точностью оценки.
Замечание Неверно говорить, что 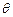 попадает в интервал. Задача состоит в том, чтобы построить такой интервал, который бы заключал в себе
попадает в интервал. Задача состоит в том, чтобы построить такой интервал, который бы заключал в себе 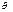 .
Доверительные интервалы строятся следующим образом:
1) вычисляется точечная оценка
.
Доверительные интервалы строятся следующим образом:
1) вычисляется точечная оценка 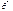 ,
2) выбирается надежность
,
2) выбирается надежность  ,
3) вычисляется точность оценки
,
3) вычисляется точность оценки  .
34. Доверительные интервалы для оценки матожидания нормального распределения при неизвестном
.
34. Доверительные интервалы для оценки матожидания нормального распределения при неизвестном  Пусть изучаемый признак Х имеет нормальное распределение. Построим по выборке
Пусть изучаемый признак Х имеет нормальное распределение. Построим по выборке 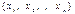 доверительный интервал для оценки математического ожидания
доверительный интервал для оценки математического ожидания 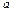 .Несмещенной и состоятельной оценкой матожидания является выборочное среднее значение
.Несмещенной и состоятельной оценкой матожидания является выборочное среднее значение  . 1. Значение параметра
. 1. Значение параметра 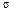 известно. Доверительный интервал будет иметь вид
известно. Доверительный интервал будет иметь вид  Здесь n – объем выборки. Точность оценки
Здесь n – объем выборки. Точность оценки
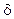 =
= 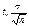 , где значение числа
, где значение числа  находится с помощью таблиц функции Лапласа из уравнения
находится с помощью таблиц функции Лапласа из уравнения  .
33. Доверительные интервалы для оценки математического ожидания нормального распределения при известном σ
Пусть
.
33. Доверительные интервалы для оценки математического ожидания нормального распределения при известном σ
Пусть 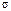 неизвестно.
В этом случае доверительный интервал будет иметь аналогичный вид, только вместо
неизвестно.
В этом случае доверительный интервал будет иметь аналогичный вид, только вместо 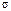 нужно подставить его оценку:
нужно подставить его оценку: 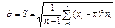 .
В результате доверительный интервал имеет вид
.
В результате доверительный интервал имеет вид  В этом случае
В этом случае 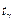 определяется по таблице распределения Стьюдента на основании
определяется по таблице распределения Стьюдента на основании 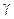 и числа степеней свободы
и числа степеней свободы  .
Так как при
.
Так как при 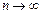 распределение Стьюдента быстро стремится к нормальному, то при больших объемах выборки (
распределение Стьюдента быстро стремится к нормальному, то при больших объемах выборки ( ) при нахождении
) при нахождении
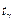 можно пользоваться таблицей функции Лапласа.
44. Проверка гипотез о достоверности коэффициента корреляции.
Пусть на выборке объема n найден коэффициент корреляции X и Y и он отличен от 0. Возможно, при этом, что генеральный коэффициент корреляции равен 0, а выборочное отличие от 0 случайно.
Проверим
H0:
можно пользоваться таблицей функции Лапласа.
44. Проверка гипотез о достоверности коэффициента корреляции.
Пусть на выборке объема n найден коэффициент корреляции X и Y и он отличен от 0. Возможно, при этом, что генеральный коэффициент корреляции равен 0, а выборочное отличие от 0 случайно.
Проверим
H0: 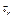 =0
H1:
=0
H1: 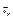
 Для проверки гипотезы H0 используем свойство T[1]
Для проверки гипотезы H0 используем свойство T[1]
 При справедливости H0 эта случайная величина имеет распределение Стьюдента с (n-2) числом степеней свободы.
Проверка H0 осуществляется следующим образом
1. вычисляется наблюдаемое значение критерия
2. по таблице критических точек распределения Стьюдента
max
При справедливости H0 эта случайная величина имеет распределение Стьюдента с (n-2) числом степеней свободы.
Проверка H0 осуществляется следующим образом
1. вычисляется наблюдаемое значение критерия
2. по таблице критических точек распределения Стьюдента
max  |Тнабл|>Tкр, то H0 отвергается и принимается H1, следовательно X и Y связаны между собой достоверной корреляционной зависимостью.
|Тнабл|<Tкр, нет основания отвергнуть H0, то
|Тнабл|>Tкр, то H0 отвергается и принимается H1, следовательно X и Y связаны между собой достоверной корреляционной зависимостью.
|Тнабл|<Tкр, нет основания отвергнуть H0, то 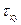 недостоверно отличается от 0 (случайно) и между X и Y нет корреляционной зависимости.
Методика построения уравнения регрессии
недостоверно отличается от 0 (случайно) и между X и Y нет корреляционной зависимости.
Методика построения уравнения регрессии

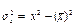
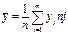
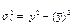
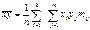

 Следующая гипотеза
H0: S21=S22
Сравнение дисперсий всегда осуществляется путем вычисления их отношения. Можно показать, что при H0 эта случайная величина имеет распределение Фишера с k1 и k2 числом степеней свободы.
F=
Следующая гипотеза
H0: S21=S22
Сравнение дисперсий всегда осуществляется путем вычисления их отношения. Можно показать, что при H0 эта случайная величина имеет распределение Фишера с k1 и k2 числом степеней свободы.
F= 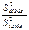 ~F(k1,k2)
Причем k1=n1-1, k2=n2-1, S21>S22
Пусть H1: S21>S22, т.е. правосторонняя критическая область.
Fk(Kкр)=1-α
Проверка H0 осуществляется следующим образом:
Вычисляется наблюдаемое значение критерия,
Выбирается уровень значимости αи по таблице критических точек распределения Фишера находят Fкр(α,k1,k2)
Если Fнабл> Fкр, то H0 отвергаем и принимаем конкурирующую.
2. Пусть H1: S21
~F(k1,k2)
Причем k1=n1-1, k2=n2-1, S21>S22
Пусть H1: S21>S22, т.е. правосторонняя критическая область.
Fk(Kкр)=1-α
Проверка H0 осуществляется следующим образом:
Вычисляется наблюдаемое значение критерия,
Выбирается уровень значимости αи по таблице критических точек распределения Фишера находят Fкр(α,k1,k2)
Если Fнабл> Fкр, то H0 отвергаем и принимаем конкурирующую.
2. Пусть H1: S21  S22 -. двусторонняя критическая область.
В этом случае поступают аналогично, только Fкр(α/2,k1,k2)
S22 -. двусторонняя критическая область.
В этом случае поступают аналогично, только Fкр(α/2,k1,k2)
 ;
;  -общая средняя.
Разложим общую сумму квадратов отклонений на факторную и остаточную
-общая средняя.
Разложим общую сумму квадратов отклонений на факторную и остаточную 
 -остаточная сумма квадратов отклонений, она обусловлена влиянием случайных величин. Характеризует рассеяние внутри группы.
-остаточная сумма квадратов отклонений, она обусловлена влиянием случайных величин. Характеризует рассеяние внутри группы. 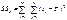 -факторная сумма квадратов отклонений. Характеризует рассеяние между группами.
Т.о.
-факторная сумма квадратов отклонений. Характеризует рассеяние между группами.
Т.о.  Построим дисперсию по каждой из этих сумм
Построим дисперсию по каждой из этих сумм
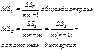
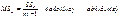 Для сравнения факторных и остаточных дисперсий построим их математического ожидания.
Для сравнения факторных и остаточных дисперсий построим их математического ожидания.  Для справедливости H0 F=0 и чем больше F значение отличное от нуля, тем больше факторная дисперсия. 30.Точечное оценивание.Пусть вид распределения изучаемого признака Х известен
Для справедливости H0 F=0 и чем больше F значение отличное от нуля, тем больше факторная дисперсия. 30.Точечное оценивание.Пусть вид распределения изучаемого признака Х известен 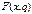 , но неизвестно значение входящего параметра
, но неизвестно значение входящего параметра  (тетта).
Статистической оценкой называется любая функция выборки
(тетта).
Статистической оценкой называется любая функция выборки
 .
Точечной оценкой называется оценка, которая дается одним числом.
Для того, чтобы статистическая оценка давала хорошее приближение оцениваемому параметру
.
Точечной оценкой называется оценка, которая дается одним числом.
Для того, чтобы статистическая оценка давала хорошее приближение оцениваемому параметру  , она должна обладать определенными свойствами.
Оценка
, она должна обладать определенными свойствами.
Оценка  называется несмещенной, если ее матожидание равно оцениваемому параметру
называется несмещенной, если ее матожидание равно оцениваемому параметру  . Несмещенной и состоятельной оценкой матожидания является выборочное среднее значение
. Несмещенной и состоятельной оценкой матожидания является выборочное среднее значение  .
Пусть
.
Пусть 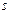 неизвестно.
В этом случае доверительный интервал будет иметь аналогичный вид, только вместо
неизвестно.
В этом случае доверительный интервал будет иметь аналогичный вид, только вместо 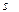 нужно подставить его оценку:
нужно подставить его оценку:  .
.  определяется на основании распределения Стьюдента из Ур-ния
2 S(x;n-1)d=
определяется на основании распределения Стьюдента из Ур-ния
2 S(x;n-1)d= 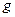 x
Где S(x;n-1) плотность распр Ст с числом степеней свободы
x
Где S(x;n-1) плотность распр Ст с числом степеней свободы  .
Так как при
.
Так как при  распределение Стьюдента быстро стремится к нормальному, то при больших объемах выборки (
распределение Стьюдента быстро стремится к нормальному, то при больших объемах выборки ( ) при нахождении
) при нахождении 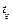 можно пользоваться таблицей функции Лапласа.Мин объем выборки кот обеспечивает задонную надежность и точность округл до ближайшего целого числа с избытком
можно пользоваться таблицей функции Лапласа.Мин объем выборки кот обеспечивает задонную надежность и точность округл до ближайшего целого числа с избытком
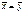 Поэтому H0 можно сформулировать, что средние равны.
Поэтому H0 можно сформулировать, что средние равны.
 Если σ неизвестно, то вместо них нужно подставить оценки
Если σ неизвестно, то вместо них нужно подставить оценки
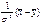 =
= 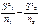 Наблюдаемое значение критерия
T=
Наблюдаемое значение критерия
T=  В этом случае случайная величина T имеет распределение Стьюдента с (n1+n2-2) числом степеней свободы.
Tn~T(n1+n2-2)
Проверка гипотезы осуществляется с использованием таблиц распределения Стьюдента по выбранному уровню значимости α и числу степеней свободы (n1+n2-2).
T кр(α, n1+n2-2)
Если |Tн|>|Tкр|, то H0 отвергаем и принимает конкурирующую гипотезу, следовательно средние в группах различаются достоверно.
Замечание 1.
Критерий Стьюдента применяется, когда n>30.
Замечание 2.
Критерий Стьюдента является устойчивым к нарушению нормального распределения изучаемых выборок. В этом случае необходимо только иметь запас уровня значимости.
Если бы мы могли отвергнуть H0 при α=0.001, то можно согласиться со следующими выводами (есть отклик на воздействие).
36. Построение критической области.
Рассмотрим построение правосторонней критической области.
Пусть вид распределения критерия К для проверки H0 известен и его плотность
В этом случае случайная величина T имеет распределение Стьюдента с (n1+n2-2) числом степеней свободы.
Tn~T(n1+n2-2)
Проверка гипотезы осуществляется с использованием таблиц распределения Стьюдента по выбранному уровню значимости α и числу степеней свободы (n1+n2-2).
T кр(α, n1+n2-2)
Если |Tн|>|Tкр|, то H0 отвергаем и принимает конкурирующую гипотезу, следовательно средние в группах различаются достоверно.
Замечание 1.
Критерий Стьюдента применяется, когда n>30.
Замечание 2.
Критерий Стьюдента является устойчивым к нарушению нормального распределения изучаемых выборок. В этом случае необходимо только иметь запас уровня значимости.
Если бы мы могли отвергнуть H0 при α=0.001, то можно согласиться со следующими выводами (есть отклик на воздействие).
36. Построение критической области.
Рассмотрим построение правосторонней критической области.
Пусть вид распределения критерия К для проверки H0 известен и его плотность  .
Критическую точку найдем из определения уровня значимости
.
Критическую точку найдем из определения уровня значимости
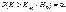
 α мы выбираем сами,
α мы выбираем сами, 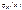 известно, тогда
известно, тогда  можно найти из уравнения Критическую точку также можно найти по функции распределения
можно найти из уравнения Критическую точку также можно найти по функции распределения  так как
так как 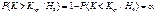 Рассмотрим построение двусторонней симметричной критической области
Рассмотрим построение двусторонней симметричной критической области  .
Пусть плотность критерия К является четной функцией. Раскроем знак модуля и перейдем к правосторонней критической области
.
Пусть плотность критерия К является четной функцией. Раскроем знак модуля и перейдем к правосторонней критической области
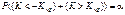
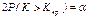

 Двусторонняя критическая симметричная область
Двусторонняя критическая симметричная область
 , но неизвестно значение входящего параметра
, но неизвестно значение входящего параметра 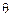 (тета).
Статистической оценкой называется любая функция выборки
(тета).
Статистической оценкой называется любая функция выборки
 = f(x1,x2,…,xn.).
Точечной оценкой называется оценка, которая дается одним числом.
Для того, чтобы статистическая оценка давала хорошее приближение к оцениваемому параметру
= f(x1,x2,…,xn.).
Точечной оценкой называется оценка, которая дается одним числом.
Для того, чтобы статистическая оценка давала хорошее приближение к оцениваемому параметру 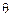 , она должна удовлетворять определенным требованиям: несмещенность, состоятельность и эффективность.Оценка
, она должна удовлетворять определенным требованиям: несмещенность, состоятельность и эффективность.Оценка 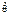 называется несмещенной, если ее матожидание равно оцениваемому параметру
называется несмещенной, если ее матожидание равно оцениваемому параметру 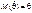 .Примеромнесмещенной оценки являетсявыборочное среднее для матожидания. Докажем это. Выборочное значение
.Примеромнесмещенной оценки являетсявыборочное среднее для матожидания. Докажем это. Выборочное значение 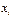 можно рассматривать как независимые случайные величины, взятые из одного и того же распределения. Пусть
можно рассматривать как независимые случайные величины, взятые из одного и того же распределения. Пусть 
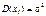

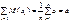 .
Примером смещенной оценки является выборочная дисперсия для теоретической дисперсии, можно показать, что
.
Примером смещенной оценки является выборочная дисперсия для теоретической дисперсии, можно показать, что 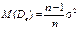 .
Для того, чтобы получить несмещенную оценку
.
Для того, чтобы получить несмещенную оценку  вводится понятие исправленной выборочной дисперсии.
вводится понятие исправленной выборочной дисперсии.
 .
.
 Оценка
Оценка 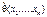 параметра
параметра  называется состоятельной, если для любого
называется состоятельной, если для любого 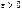
 Состоятельность оценки означает, что при большом объеме выборки оценка приближается к истинному значению параметра
Состоятельность оценки означает, что при большом объеме выборки оценка приближается к истинному значению параметра  (чем больше n, тем точнее оценка).
Оценки, обладающие свойством несмещенности и состоятельности, при ограниченном объеме выборки могут отличатся дисперсиями.
Чем меньше дисперсия оценки, тем меньше вероятность ошибки при вычислении
(чем больше n, тем точнее оценка).
Оценки, обладающие свойством несмещенности и состоятельности, при ограниченном объеме выборки могут отличатся дисперсиями.
Чем меньше дисперсия оценки, тем меньше вероятность ошибки при вычислении 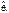 Поэтому целесообразно, чтобы дисперсия оценки была минимальной, т.е. чтобы выполнялось условие
Поэтому целесообразно, чтобы дисперсия оценки была минимальной, т.е. чтобы выполнялось условие 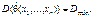 Оценка, обладающая таким свойством, называется эффективной.
32. Распределение
Оценка, обладающая таким свойством, называется эффективной.
32. Распределение  , Стьюдента и Фишера.
Распределение
, Стьюдента и Фишера.
Распределение  (хи-квадрат).Пусть
(хи-квадрат).Пусть  независимы и имеют стандартное нормальное распределение. Тогда случайная величина
независимы и имеют стандартное нормальное распределение. Тогда случайная величина 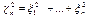 называется распределённой по закону
называется распределённой по закону  с n степенями свободы. Математическое ожидание и дисперсия распределения
с n степенями свободы. Математическое ожидание и дисперсия распределения  равны:
равны: 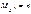 ,
, 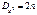 График – плотность распределения
График – плотность распределения  .При n
.При n 
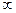 распределение
распределение 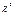 медленно стремится к нормальному.
медленно стремится к нормальному.
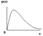
 Распределение Стьюдента.Пусть
Распределение Стьюдента.Пусть 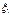 и
и 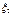 независимы и
независимы и 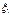 имеет стандартное нормальное распределение, а
имеет стандартное нормальное распределение, а  - распределение
- распределение 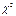 с k степенями свободы. Тогда случайная величина
с k степенями свободы. Тогда случайная величина  называется распределённой по закону Стьюдентас k степенями свободы.График – плотность распределения
Стьюдента. При k
называется распределённой по закону Стьюдентас k степенями свободы.График – плотность распределения
Стьюдента. При k  распределение Стьюдента быстро стремится к нормальному. Математическое ожидание и дисперсия распределения Стьюдента – MT=0, DT=
распределение Стьюдента быстро стремится к нормальному. Математическое ожидание и дисперсия распределения Стьюдента – MT=0, DT=  .
Распределение Фишера.Пусть
.
Распределение Фишера.Пусть  и
и 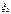 независимы и имеют распределение
независимы и имеют распределение 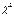 с
с  и
и  числом степеней свободы соответственно. Тогда случайная величина
числом степеней свободы соответственно. Тогда случайная величина 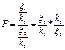 называется распределённой по закону Фишераc
называется распределённой по закону Фишераc  и числом степеней свободы.
и числом степеней свободы.
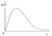 График – плотность распределения Фишера. Замечание. Табличные значения случайной величины Фишера всегда больше 1.
График – плотность распределения Фишера. Замечание. Табличные значения случайной величины Фишера всегда больше 1.