Доказательство. Доказательство окончено

ТЕОРЕМА 6.3

Доказательство окончено.

СЛЕДСТВИЕ 2

СЛЕДСТВИЕ 1

Доказательство окончено.

Для всякой транспортной сети величина максимального потока равна минимуму пропускных способностей сечений этой сети.

Пусть N = (G, c) - транспортная сеть с функцией пропускной способности, принимающей рациональные значения.

Тогда для N существует максимальный поток.

Доказательство

Пусть рациональные значения пропускных способностей ребер u ₁,..., u_m транспортной сети N = (G, c) задаются как отношения неотрицательных целых чисел p ₁/ q ₁,..., p_m / q_m.

Пусть d = q ₁ ´... ´ q_m.

Рассмотрим сеть N ^* = (G, c ^*), для которой c ^* = d´c. Поскольку функция c ^* принимает только целочисленные значения, то для N ^* существует максимальный поток y^*.

Тогда поток y = y^*\ d является максимальным потоком для транспортной сети N.

Действительно, сечение L для G, пропускная способность которого в сети N ^*совпадает с величиной потока y^*, в сети N имеет пропускную способность, совпадающую с величиной потока y. Поэтому y - это максимальный поток.

Для всякой транспортной сети существует максимальный поток.

Пусть N = (G, c) - это произвольная транспортная сеть. Рассмотрим последовательность рациональнозначных функций пропускной способности ребер сети N: c ₁,..., c_i,..., которые равномерно сходятся к функции c снизу.

Из следствия 2 следует, что для транспортных сетей
N_i = (G, c_i), i = 1,... существуют максимальные потоки

y₁,..., y _i,... (1)

Пусть сеть N содержит ребра u ₁,..., u_m.

Из последовательности (1) выделим такую бесконечную подпоследовательность потоков

y_1,1..., y_1,j,... (2),

что числовая последовательность y₁, _i (u ₁), i = 1, 2,...
является сходящейся.

Из последовательности (2) выделим подпоследовательность

y₂,₁,..., y₂, _j... (3).

Для (3) числовая последовательность y₂ ,_j (u ₂), j = 1, 2,...также является сходящейся.

Продолжая процесс выделения подпоследовательностей, через конечное число шагов получаем последовательность функций

y_m, ₁,..., y_m, _j,... (m).

Эта последовательность состоит из потоков, значения которых на каждом ребре сети образуют сходящиеся последовательности.

Пусть y .

1. Покажем, что y является потоком.

Поскольку для всякого потока y_m ,_j справедливо неравенство

y_m ,_j 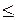c _{m, j}, то 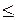c.

Кроме того, для всякого потока y_m, _j и внутренней вершины a сети N _m, _j выполняется равенство

.

Предельный переход по j ® ¥ преобразует последнее равенство в равенство

.

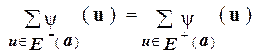Следовательно, y является потоком в N.

2. Покажем, что y - это максимальный поток.

Если c _m, _j - функция пропускной способности, отличающаяся от c на всех ребрах сети не более чем на e, то величина всякого потока в транспортной сети N не превосходит величины y + k ´ e, где k - число ребер, выходящих из истока сети.

Поскольку значение e можно выбрать сколь угодно малым, то величина всякого потока в N не превосходит значения величины потока y. Следовательно, y - это максимальный поток.

Доказательство окончено.

Дата добавления: 2015-03-31