Монотонность. -биноминальный коэффициент

Ограниченность.

-биноминальный коэффициент.

+ <

+ .

…

.

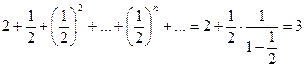
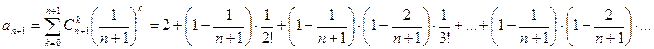
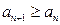По теореме о монотонности последовательности 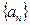- сходится.

12) Лемма о вложенных отрезках.

Лемма о вложенных отрезках.

Последовательность отрезков { }={[ , 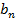]} наз-ся послед. Вложенных отрезков, если

> для любого n.

Лемма. { } =={[an,bn]} посл-ть вложенных отрезков, причем {dn} стремится к нулю, где dn=bn-an.

Тогда существует единственная C принадлежащая множеству вещественных чисел, С для любого n.

Док-во. Обозначим A={a1,a2,a3...}- мн-во левых концов отрезка. B={b1,b2,b3...}-мн-во правых концов отрезка, заметим, что A .

Док-м что .

1. =>

=> =>

2. =>

=> =>

След-но A, B – непустые мн-ва, т.ч. , => по св-вам действительных чисел В частности при =>

, .

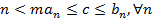Д-м, что C- единственная точка, принадлежащая другим отрезкам. Предположим, что => .

Пусть, например,

.

=> => ->0 => по св-вам пределов , но , при nстремящемся к бесконечности => => => => 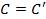C-единственная точка

Замечание. Заметим, что С=sup A(inf A).

Д-м, что C=sup A => C-верхняя грань A.

Нужно док-ть что C-наименьшая верхняя грань A.

Предположим, что C- не наименьшая верхняя грань,т. е. Существует верхняя грань : =>

Повторим док-во леммы (см. И С) получаемЮ что - получаем противоречие с выбором , след-но С наименьшая верхняя грань A, C=sup A.Аналогично док-ся, что C=inf B.

13) Подпоследовательности, частичные пределы. Связь предела последовательности с частичными пределами.

Билет № 13. Подпосл-ти, частичные пределы, связь предела посл-тей с частичным пределом.

Пусть дана посл-ть { }. Выбираем элементы с номером < < < => числа { , , ,…} образуют посл-ть { }.

Утверждение. 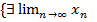=a}ó{для любой её подпосл-ти { } }.

Доказательство. => =a =>

Рассмотрим }.

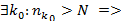| -a|< .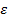

Таким образом =>

<= Для } =a.

{ } также подпосл-ть посл-ти { }=> .

Замечание 1. Аналогичное утверждение для бесконечно больших посл-тей, т.е. посл-ть { } явл. б.б. => } явл. б.б.

Замечание 2. Пусть { } имеет две сх-ся подпосл-ти { } и { }, такие что , тогда .

Предположим противное, т.е. =a => тогда по теорме =a, получаем противоречие, след-но .

Частичный предел пол-ти.

Определение. Бесконечный и конечный предел определённого знака наз-ся частичным пределом посл-ти { }.

Понятие о верхнем и нижнем пределе.

Мн-во действительных чисел R, заполненное эл-ми {+ } и {- } пределов, наз-ся расширенным мн-вом действительных чисел.

Определение. Наибольшим в частичный предел посл-ти наз-ся её верхним пределом и обозначается . Наименьшим в частичным пределом посл-ти наз-ся её нижним пределом и обозначается .

14) Теорема Больцано-Вейерштрасса.

Теорема: Из всякой ограниченной последовательности можно выделить сходящуюся подпоследовательность.

Дата добавления: 2015-04-23