Основные даты и события. 2 страница

= * * = .

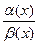1 1

27) Сравнение б.б. функций. Примеры.

28) Непрерывность функции в точке (3 определения). Свойства функций, непрерывных в точке.

Определение 1: Функция 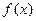непрерывна в точке 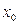, если .

Определение 2: Функция 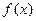непрерывна в точке 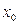, если , .

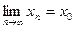Определение 3: Функция 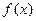непрерывна в точке 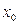, если

.

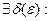
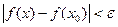Свойства непрерывных функций:

Теорема 1 (локальная огр.): Пусть функция 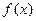непрерывна в точке 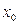, тогда .

Теорема 2 (отделимость от 0): Пусть функция 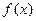непрерывна в точке 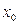и , тогда

. .

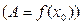Теорема 3 (арифметика непрерывных функций): Пусть 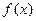, 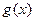непрерывны в точке 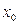, тогда:

1). 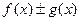непрерывна в точке .

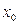2). 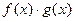непрерывно в точке .

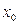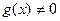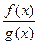3). Если , то непрерывно в точке .

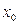29) Непрерывность сложной функции.

Теорема: если функция 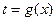непрерывна в точке , а функция непрерывна в точке 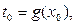то сложная функция 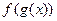непрерывна в точке .

Доказательство:

Возьмем число 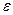>0. Так как функция непрерывна в точке 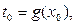то можно подобрать такое число , что

для любого 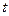, такого, что . (1)

А так как функция 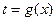непрерывна в точке , то для положительного числа 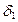можно подобрать такое число , что

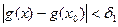для любого 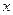, такого, что . (2)

Возьмем любое число 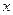такое, что . Тогда в силу (2) число 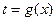удовлетворяет неравенству 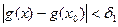, и поэтому в силу (1) . Так как все эти вычисления проведены для любого 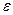>0, то непрерывность функции 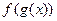в точке доказана.

30) Классификация точек разрыва.

Определение: -точка разрыва функции , если в точке функция не является непрерывной.

Определение: точка -точка устранимого разрыва функции , если существует , но не определена в точке , либо .

Замечание: Если в точке устранимого разрыва доопределить (переопределить) функцию:

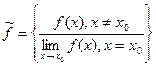- непрерывна в точке .

Пример: .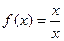

, - точка устранимого разрыва .

Если не существует, то -точка неустранимого

разрыва .

Определение: Пусть точка -точка неустранимого разрыва функции , тогда:

1) если существует 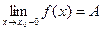, то .

2) если 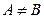, то -точка разрыва функции 1-го рода.

3) если 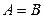, то -точка разрыва функции 2-го рода.

Примеры:

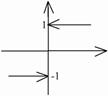
1). .

,

- точка разрыва 1-го рода.

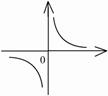2). .

,

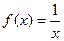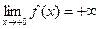- точка разрыва 2-го рода.

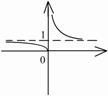3).

,

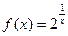
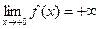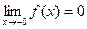
- точка разрыва 2-го рода.

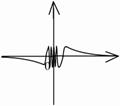4).

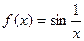
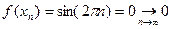
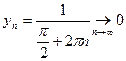
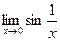не существует точка - точка разрыва 2-го рода.

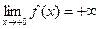, . Точка - точка разрыва 2-го рода.

31) Точки разрыва монотонной функции.

32) Первая теорема Вейерштрасса.
Пусть . Тогда ограничена на .

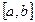Доказательство:

Докажем, что .

Предположим противное, то есть 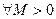. Возьмем =1,2,3…

Получим :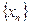

1)

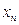
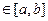
2)

Из этих определений получаем .

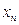
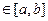=> -подпоследовательность последовательности :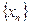

.

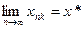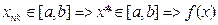-непрерывна в точке => .

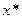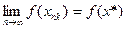-подпоследовательность последовательности 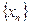: => . Противоречие.

Замечание: Замкнутость по существу. , , но

Не является ограниченной на .

33) Вторая теорема Вейерштрасса.

Пусть . Тогда

Замечание: Непрерывная на отрезке 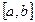функция на этом отрезке достигает своего наибольшего и наименьшего значения, причем в условиях теоремы отрезок по существу.

Доказательство:

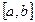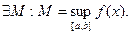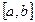
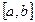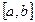По условию теоремы => ограничена на => Докажем, что . Предположим противное, то есть . Рассмотрим вспомогательную функцию на . По 1 теореме Вейерштрасса ограничена на , то есть .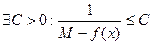

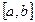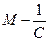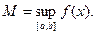(< )- верхняя граница. , то есть .

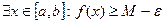Противоречие.

Следствие: если , то .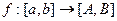

34) Теорема о нуле непрерывной функции.

35) Теорема Больцано-Коши, ее следствия.

36) Критерий непрерывности монотонной функции.

37) Непрерывность обратной функции.

862 - призвание Рюрика,

862-879 - годы правления Рюрика,

879-912 - годы правления Олега,

907, 911 - походы Олега на Византию,

912-945 - годы правления Игоря,

941, 944 - походы Игоря на Византию,

945 - убийство Игоря древлянами,

945-972 - годы правления Святослава,

945-964 - годы регентства Ольги,

965 - покорение Хазарского каганата,

968 - победа над Волж­ской Булгарией,

972 – 980 - годы правления Ярополка,

980-1015 - годы правления Владимира,

988 - принятие хри­стианства,

1015 – 1019 - годы правления Святополка I Окаянного,

1019-1054 - годы правления Ярослава Мудрого,

1054 - разделение единой христианской церкви на православную и

католическую,

1054 - … - 1078 - годы правления Изяслава I,

1078-1093 - годы правления Всеволода I,

1093-1113 - годы правления Святополка II,

1097 - съезд в Любече,

1113 – 1125 - годы правления Владимира Мономаха

Образование древнерусского государства. Существует несколько теорий возникновения государства у восточных славян.

1. Славянская (антинорманнская). Отрицается роль варя­гов в образовании древнерусского госу­дарства и призвание их на княжение (М.В. Ломоносов).

2. Норманнская. Древнерусское госу­дарство создано нор­маннами (варягами) с добровольного согла­сия славян (Г. Байер, А. Шлецер, Г. Миллер).

3. Центристская (современная). Древнерусское госу­дарство возникло как результат внут­реннего обществен­ного развития сла­вян, но и при уча­стии варягов (большинство современных историков).

Дата добавления: 2015-04-23