Криптография с открытым ключом (несимметричные шифры). Однонаправленная функция и однонаправленная функция с секретом. Проблема существования однонаправленной функции

Шифр одноразовый блокнот. Поточные шифры и задача генерации равномерно распределенных псевдослучайных чисел. Линейный конгруэнтный генератор псевдослучайных чисел и его криптоанализ.

Поточные шифры – выполняют криптографическое преобразование побитово: каждый символ открытого текста преобразуется в символ шифрованного текста в зависимости не только от используемого ключа, но и от его расположения в потоке открытого текста. Поточный шифр реализует другой подход к симметричному шифрованию, нежели блочные шифры.

Одноразовый блокнот – зашифрованный текст получается путем операции XOR(«исключающее или») открытого текста с результатом преобразования ключа. Это преобразование должно приводить ключ к произвольной длине открытого текста и по сути решает проблему генерации псевдослучайных чисел на основе данного ей ключа. Одним из вариантов решения подобной задачи является линейный конгруэнтный генератор псевдослучайных чисел:

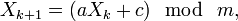
который получает каждое следующее псевдослучайное число на основе предыдущего (а первое на основе собственно ключа). Его главный недостаток в том, что зная всего два из этих чисел (а их можно узнать использую атака по парам открытый/зашифрованный текст), можно вычислить «а» и «с» – а потом пройти по последовательности назад вплоть до исходного ключа.

25. Генерация псевдослучайных последовательностей. Регистры сдвига с линейной обратной связью (РСЛОС): общая схема, математическое описание, пример генерации гаммы, период, РСЛОС с максимальным периодом, криптоанализ.

Генератор псевдослучайных чисел — алгоритм, порождающий последовательность чисел, элементы которой почти независимы друг от друга и подчиняются заданному распределению (обычно равномерному).

Альтернатива линейному конгруэнтному генератору более стойкая к криптоанализу – это регистр сдвига с линейной обратной связью:

Общая схема регистра сдвига с линейной обратной связью

Математическое описание:

В качестве функции обратной связи берётся логическая операция XOR (исключающее ИЛИ), то есть:

• на первом шаге:
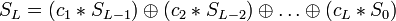
• на втором шаге:
• …
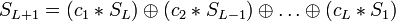
• на j − L − 1-м шаге:

Где каждый коэффициент с_i - это либо 0, либо 1.

Пример: Пусть имеется четыре регистра, начальные значения которых A1=1, A2=0, A3=0. A4=0. Коэффициенты С имеют значения C1=1,C2=0, С3=1, C4=1 реализуя уравнение: . Тогда псевдослучайная последовательность примет вид:

Номер шага	A1	A2	A3	A4	S	Выход системы
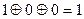
						нет

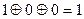
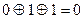
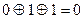
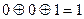
- как видно из таблицы за 6 шагов система вернулась к начальному состоянию. Следовательно ее период равен 6. (А максимальный мог бы быть 15)

Так как существует 2L − 1 разных ненулевых состояний регистра, то период последовательности, генерируемой РСЛОС при любом ненулевом начальном состоянии, не превышает 2L − 1. При этом период зависит от ассоциированного многочлена:

• если старший коэффициент ассоциированного многочлена CL равен нулю, то периодичная часть генерируемой последовательности может проявляться не сразу;
• если CL = 1, то соответствующая последовательность называется неособой. Такая последовательность начинается со своей периодичной части. Наиболее интересны неособые последовательности, соответствующие многочленам со следующими дополнительными свойствами:
• если C(x) неприводим, то при любом ненулевом начальном состоянии регистра период генерируемой последовательности равен наименьшему числу N, при котором многочлен C(x) делит 1 + xN. Как следствие, период последовательности будет делить число 2L − 1;
• если C(x) примитивен (то есть, является делителем 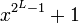, но не является делителем xd + 1 для всех d, делящих 2L − 1), то любое ненулевое начальное состояние регистра дает последовательность с максимально возможным периодом 2L − 1. Например, РСЛОС с отводной последовательностью, состоящей из первого и четвёртого битов имеет максимальный период тогда и только тогда, когда ассоциированный многочлен x⁴ + x + 1 является примитивным.

В случае криптоанализа для нахождения всех последующих чисел необходимо знать одно из них и все значения c_i.Для поиска этих значений необходимо и достаточно узнать последовательные 2n бит случайных чисел, где n – размер регистра

26. Шифр RC4 (arcfour): параметры, алгоритм развертки ключа, алгоритм генерации гаммы. Алгоритмическое и схематическое описание.

Параметры:

1. Длина ключа: от 40 до 256 бит
2. Размер n слова S-блока (стандартно 8). Размер самого S-блока определяется, как 2ⁿ

Ядро алгоритма состоит из функции генерации ключевого потока. Эта функция генерирует последовательность битов (ki), которая затем объединяется с открытым текстом (mi) посредством суммирования по модулю два. Так получается шифрограмма (ci):

.

Расшифровка заключается в регенерации этого ключевого потока (ki) и сложении его и шифрограммы (ci) по модулю два. В силу свойств суммирования по модулю два на выходе мы получим исходный незашифрованный текст(mi):

Алгоритм развертки ключа:

Его роль выполняет функция инициализации, которая использует ключ переменной длины для создания начального состояния генератора ключевого потока.

Этот алгоритм использует ключ, который подается на вход пользователем, сохранённый в Key, и имеющий длину L байт. Инициализация начинается с заполнения массива S, далее этот массив перемешивается путем перестановок, определяемых ключом. Так как только одно действие выполняется над S, то должно выполняться утверждение, что S всегда содержит один набор значений, который был дан при первоначальной инициализации (S[i]:= i).

Алгоритм генерации гаммы:

Генератор ключевого потока RC4 переставляет значения, хранящиеся в S, и каждый раз выбирает различное значение из S в качестве результата. В одном цикле RC4 определяется одно n-битное слово K из ключевого потока, которое в последующем суммируется с исходным текстом для получения зашифрованного текста

Алгоритмическое описание:

Начальное заполнение массива:

for i = 0 to 2ⁿ − 1

S[ i ] = i

Скремблирование:

j = 0

for i = 0 to 2ⁿ − 1

j = (j + S[ i ] + Key[ i mod L ]) mod 2n
Перестановка местами(S[ i ], S[ j ])

Инициализация:

i = 0

j = 0

Цикл генерации:

i = (i + 1) mod 2n

j = (j + S[ i ]) mod 2n

Перестановка местами (S[ i ], S[ j ])

K = S[ (S[ i ] + S[ j ]) mod 2ⁿ ]

Схематическое описание:

27. Шифр A5/1: параметры, схема, мажоритарная функция, алгоритм работы при шифровании кадра.

Параметры:

1. Длина сессионного ключа
2. Длина кадра
3. Длина номера кадра.(число кадров)

Схема алгоритма:

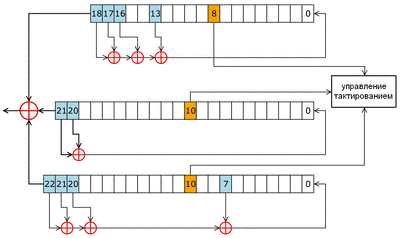
Структура алгоритма А5/1 выглядит следующим образом:

• три регистра(R1, R2, R3) имеют длины 19, 22 и 23 бита,
• многочлены обратных связей:
• X18 + X17 + X17 + X13 + 1 для R1,
• X21 + X20 + 1 для R2 и
• X22 + X21 + X20 + X7 + 1 для R3,
• управление тактированием осуществляется специальным механизмом (мажоритарной функцией):
• в каждом регистре есть биты синхронизации: 8 (R1), 10 (R2), 10 (R3),
• вычисляется функция 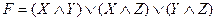(мажоритарная функция), где X, Y и Z — биты синхронизации R1, R2 и R3 соответственно,
• сдвигаются только те регистры, у которых бит синхронизации равен F,
• фактически мажоритарная функция выбирает те регистры, значения которых принадлежат к большинству (то есть, если у всех трех значения равны – будут сдвинуты все, если же равны значения только у двух из трех, то сдвинуты будут только они)
• выходной бит системы — результат операции XOR над выходными битами регистров.

Функционирование алгоритма А5

Рассмотрим особенности функционирования алгоритма, на основе известной схемы. Передача данных осуществляется в структурированном виде — с разбивкой на кадры (114 бит). При инициализации алгоритма, на его вход поступают сессионный ключ (K — 64 бита), сформированный А8, и номер кадра (Fn — 22 бита). Далее последовательно выполняются следующие действия:

• инициализация:
• 64 такта без управления сдвигами регистров, при которых младшие биты складываются с соответствующим битом сессионного ключа,
• аналогичные 22 такта, только суммирование производится с номером кадра,
• 100 тактов с управлением сдвигами регистров, но без генерации последовательности,
• 228 (114 + 114) тактов рабочие, происходит шифрование передаваемого кадра (первые 114 бит) и дешифрование (последние 114 бит) принимаемого,
• далее инициализация производится заново, используется новый номер кадра.

28. Массовая задача, алгоритм, сложность алгоритма. Детерминированная и недетерминированная машина Turing. Классы сложности P и NP. Сводимость задач. NP-полная задача: пример. Гипотеза и криптография.

Массовая задача – объединение всех возможных однотипных единичных задач

Алгоритм – решение массовой задачи.

Алгоритм характеризуется временной и пространственной сложностью. (Сложность может быть задана через символ O, как ограниченная сверху полиномиальной, экспоненциальной и т. д. функцией)

Детерминированная машина Тьюринга состоит из бесконечной памяти, вычислительного устройства и устройства ввода/вывода в память.

К ней применимы следующие команды:

1. Сдвинуть устройства ввода/вывода вдоль ленты в одну или другую сторону
2. Прочитать данные с ленты
3. Записать данные на ленту.

Алгоритмы для Машины Тьюринга могут быть записаны в виде детерминированного автомата, где машина обладает внутренними состоянием, а символы, считываемые с ленты изменяют этот состояние. При переходе между состояниями производятся соответствующие записи на ленту и/или сдвиги устройства ввода/вывода. Этот автомат описывается набором функций перехода, которые в ответ на два входных значения(состояние и считанный символ), возвращают три выходных(новое состояние, направление сдвига и записываемый символ).

Недетерминированная Машина Тьюринга соответственно описывается недетерминированным автоматом, где для одного и того же состояния, один и тот же входной символ может вести в несколько разных новых состояний.

P класс – задачи решаемые на ДМТ за полиномиальное время

NP класс – задачи решаемые на НДМТ за полиномиальное время

Сводимость задач – это возможность за полиномиальное время переформулировать одну задачу к другой. Если задача может быть сведена к Р задаче – она также Р. Если задача сводится к NP задаче – то она также NP.

NP полная задача – это такая задача, что

1. Она сама NP задача
2. Любая другая NP задача может быть сведена к ней за полиномиальное время.

Пример:

Задача SAT(выполнимости булевых формул) – проверяющая можно ли для данной булевой формулы подобрать такие аргументы, что она примет значение истина

Криптография с открытым ключом использует тот факт, что NP задачи не решаемы за приемлемое время. Но то, что они не могут быть решены за полином (то есть что они не сводимы к P задачам, P<>NP) – только гипотеза и в случае его опровержения все алгоритмы, основанные на ней, окажутся бессмысленными.

Криптография с открытым ключом – ключи не могут быть получены один из другого простым преобразованием, и один из них можно опубликовать, сохранив второй при этом в секрете.

Однонаправленная функция: прямое преобразование в ней – это Р задача, а вот обратная функция к ней - это NP задача

Однонаправленная функция с секретом: прямое преобразование – это Р задача, а обратное NP задача, если неизвестен секрет, с помощью секрета обратная функция тоже сводится к Р задаче. (Очевидно, что вычисление секрета –это и есть NP-часть задачи)

Если ключи шифрования и расшифровки вычисляются друг из друга, как однонаправленная функция с секретом, то достаточно держать в секрете только первый из них и секрет самой функции.

Существование однонаправленных функций до сих пор не доказано. Если f является односторонней функцией, то нахождение обратной функции является трудновычислимой (по определению), но легкопроверяемой задачей (путем вычисления f на ней). Таким образом, из существования односторонней функции следует, что P ≠ NP. Однако, не известно, влечет ли за собой P ≠ NP существование односторонних функций. Современная асимметричная криптография основывается на предположении, что односторонние функции все-таки существуют.

Пример потенциально однонаправленной функции: возведение в квадрат по модулю. Обратная к ней функция – извлечение квадратного корня по модулю – это NP задача.

30. Целые числа: делимость, свойство евклидовости, алгоритм Евклида (с примером), расширенный алгоритм Евклида (с примером).

Дели́мость — одно из основных понятий арифметики и теории чисел, связанное с операцией деления. Если для некоторого целого числа 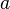и целого числа существует такое целое число , что 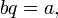то говорят, что число 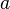делится нацело на или что делит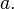

При этом число b называется делителем числа a, делимое a будет кратным числа b, а число q называется частным от деления a на b.

Алгоритм Евклида – это способ нахождения наибольшего общего делителя двух целых чисел, а также наибольшей общей меры двух соизмеримых отрезков.

Чтобы найти наибольший общий делитель двух целых положительных чисел, нужно сначала большее число разделить на меньшее, затем второе число разделить на остаток от первого деления, потом первый остаток – на второй и т.д. Последний ненулевой положительный остаток в этом процессе и будет наибольшим общим делителем данных чисел.

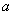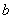Обозначив исходные числа через и , положительные остатки, получающиеся в результате делений, через 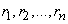, а неполные частные через 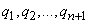, можно записать алгоритм Евклида в виде цепочки равенств:

Пример: a=54, b=15

a	b	r

НОД(54,15)=3

Расширенный алгоритм Эвклида:

Связан с так называемым соотношением Безу:

«Пусть a, b — целые числа, хотя бы одно из которых не нуль. Тогда существуют такие целые числа x, y, что выполняется соотношение: НОД(a,b) = x·a + y·b.»

Позволяет найти не только наибольший общий делитель. Но и числа x,y.

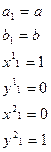
При этом значения x и y будут содержаться в x2 и y2 на том шаге, когда d окажется равным 0.

Пример: a=92, b=14

a	b	c	d	x1	x2	y1	y2
							-6
					-1	-6
				-1			-13

Проверка:

2=2*92-13*14; 2=184-182; 2=2

Дата добавления: 2015-04-24