Простое число. Количество простых чисел. Основная теорема арифметики

Простое число – это натуральное число, имеющее ровно два различных натуральных делителя: единицу и само себя.

Количество простых чисел бесконечно велико – доказательство Эвклида:

«Представим, что количество простых чисел конечно. Перемножим их и прибавим единицу. Полученное число не делится ни на одно из конечного набора простых чисел, потому что остаток от деления на любое из них даёт единицу. Значит, число должно делиться на некоторое простое число, не включённое в этот набор. Противоречие.»

Основная теорема арифметики: любое число не равное нулю или 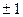может быть разложено на произведение простых чисел в некоторых степенях и такое разложение единственно.

Основная теорема арифметики может быть распространена и на другие кольца(множества с заданной операцией умножения), но в некоторых из них разложение не будет единственно.

32. Функция Эйлера. Вычисление функции Эйлера, в частности, функция Эйлера простого числа и произведения двух простых чисел: примеры.

Ф-ция Эйлера – возвращает кол-во натуральных чисел меньше ее аргумента, которые имеют с ним НОД =1(взаимно просты).

Для простого числа – возвращает значение на 1 меньше его самого(Поскольку любое число меньше простого взаимно просто с ним).

Для произведения двух простых чисел a и b: phi(a*b)=(a-1)*(b-1)

Доказательство. Очевидно, что всего натуральных чисел меньше произведения а*b ровно a*b-1. Из них все числа: 1*b,2*b,….,(a-1)*b – имеют c ab НОД=b и не являются взаимно простыми. Этих чисел b-1. Аналогично 1*a,2*a,….,(b-1)*a – имеют c ab НОД=a. Этих чисел всего a-1. Если предположить, что эти набора чисел не имеют общих элементов, то взаимно простых чисел остается ровно: ab-1-(a-1)-(b-1)=ab-a-b+1=(a-1)(b-1). Т. к. и a и b простые, то наборы чисел будут иметь общие элементы, только в случае, когда a=b и значит они совпадают тождественно и значит вычитать следует только один из них. Тогда, если a=b: phi(a*a)=a*a-a=a*(a-1)

Примеры:

phi(13)=12

phi(21)= phi(3*7)=2*6=12

phi(9)=3*(3-1)=6

33. Теорема Эйлера и ее доказательство, малая теорема Ферма: примеры.

Если a и m взаимно просты, то , где φ(m) — функция Эйлера.

Читается, как: a, возведенное в степень функции Эйлера от m, и взятое по модулю m тождественно единице.

Доказательство:

Пусть — все различные натуральные числа, меньшие m и взаимно простые с ним.

Рассмотрим всевозможные произведения x_i*a для всех i от 1 до φ(m).

Поскольку a взаимно просто с m и x_i взаимно просто с m, то и x_i*a также взаимно просто с m, то есть для некоторого j.

Отметим, что все остатки x_i*a при делении на m различны. Действительно, пусть это не так, то есть существуют такие 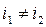, что

Или

Так как a взаимно просто с m, то последнее равенство равносильно тому, что

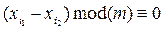или .

Это противоречит тому, что числа попарно различны по модулю m.

Перемножим все равенства . Получим:

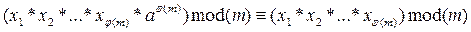
или

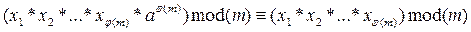
Так как число 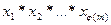взаимно просто с m, то последнее равенство равносильно тому, что

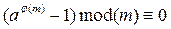
или

Пример:a=3 m=8

φ(8)=4

(3⁴) mod 8=(81) mod 8 = 1

Малая теорема Ферма – частный случай теоремы Эйлера, основывающийся на значении функции Эйлера от простого числа: если m – простое, то

34. Способы деления чисел в конечном простом поле: примеры. Алгоритм быстрого вычисления степеней числа.

Деление чисел в простом поле осуществляется путем домножения делимого на обратный элемент к делителю.

Обратный элемент вычисляется либо расширенным алгоритмом Эвклида:

Пусть нужно найти: на поле ограниченном простым числом p

Возьмем соотношение Безу для p и b: 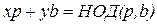. Так как p – простое, то 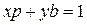. Если взять это соотношение по модулю p, то получится:

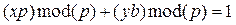, т. к. , то

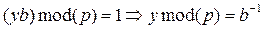
Либо, исходя из малой теоремы Ферма, т. к. то и 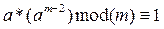, а значит

Примеры:

Расширенный алгоритм Эвлида:

a	b	c	d	x1	x2	y1	y2
							-2
					-1	-2
				-1	-2		-5

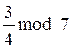
Малая теорема Ферма:

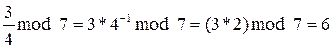
Алгоритм быстрого возведения в степень — алгоритм, предназначенный для возведения числа x в натуральную степень n за меньшее число умножений, чем это требуется в определении степени.

Рассмотрим двоичное представление степени, в которую требуется возвести число x

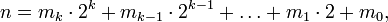
где .

Тогда алгоритм примет вид: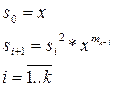

Дата добавления: 2015-04-24