
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные понятия и определения
|
|
|
|
Система m уравнений с n неизвестными вида
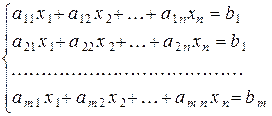
| (1) |
называется системой линейных уравнений (сокращенно СЛУ).
Неизвестные x 1, x 2, …, x n образуют вектор`x = 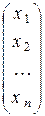 , который называется столбцом неизвестных.
, который называется столбцом неизвестных.
Коэффициенты a i j при неизвестных образуют матрицу
A =  , которая называется матрицей системы уравнений.
, которая называется матрицей системы уравнений.
Числа b 1, b 2 , …, b m образуют столбец свободных членов` b = 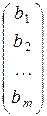 .
.
Матрица A с добавленным к ней столбцом свободных членов ` b называется расширенной матрицей и обозначается Ã:
à = 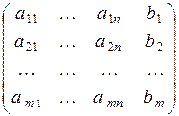 .
.
Наряду с этой матрицей будем также рассматривать матрицу
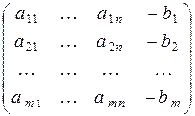 ,
,
которая получается из A добавлением к ней столбца –` b. Поскольку такая матрица будет обладать всеми свойствами матрицы Ã, ее мы тоже будем называть расширенной матрицей системы (1).
Используя введенные обозначения, систему уравнений, заданную в ее общем виде (1), можно переписать в других, более компактных видах.
МАТРИЧНЫЙ ВИД.
Умножим матрицу A на столбец неизвестных`x согласно правилу умножения матриц. Получим равенство
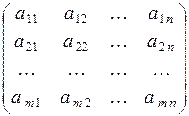 ·
· 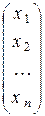 =
= 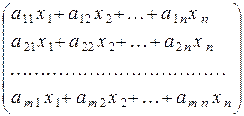 .
.
Следовательно, систему уравнений (1) можно записать в виде
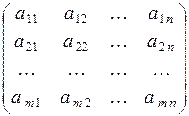 ·
· 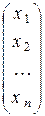 =
= 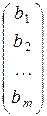 , или A`x =` b.
, или A`x =` b.
ВЕКТОРНЫЙ ВИД.
Рассмотрим векторы`A 1,`A 2 , …,`A n — столбцы матрицы A. Используя правила сложения векторов и умножения вектора на число, получим равенство x 1 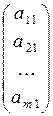 + x 2
+ x 2 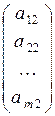 +…+ x n
+…+ x n 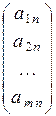 =
= 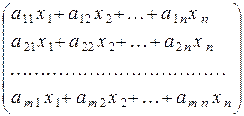 , то есть x 1`A 1 + x 2`A 2 + … + x n `A n =` b — векторный вид системы уравнений (1).
, то есть x 1`A 1 + x 2`A 2 + … + x n `A n =` b — векторный вид системы уравнений (1).
ТАБЛИЧНЫЙ ВИД.
Перепишем систему уравнений (1) в виде
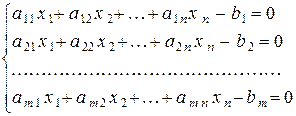 .
.
Внесем полученные соотношения в жорданову таблицу
| x 1 | x 2 | … | x n | ||
| 0 = | a 11 | a 12 | … | a 1 n | – b 1 |
| 0 = | a 21 | a 22 | … | a 2 n | – b 2 |
| … | … | … | … | … | … |
| 0 = | a m 1 | a m 2 | … | a m n | – b m |
Получили табличный вид системы уравнений.
ПРИМЕР.
Запишем в разных видах систему уравнений 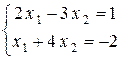 .
.
 ·
· 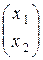 =
= 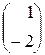 — матричный вид;
— матричный вид;
|
|
|
x 1 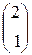 + x 2
+ x 2 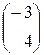 =
= 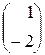 — векторный вид;
— векторный вид;
| x 1 | x 2 | — табличный вид. | ||
| 0 = | –3 | –1 | ||
| 0 = |
Вектор`x * = 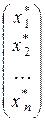 называется решением системы линейных уравнений, если при подстановке его координат в уравнения системы все уравнения обращаются в верные равенства.
называется решением системы линейных уравнений, если при подстановке его координат в уравнения системы все уравнения обращаются в верные равенства.
Система уравнений называется совместной, если она имеет хотя бы одно решение.
Система уравнений называется несовместной, если она не имеет ни одного решения.
Система уравнений называется определенной, если она имеет ровно одно решение.
Система уравнений называется неопределенной, если она имеет более одного решения.
2. СИСТЕМЫ n ЛИНЕЙНЫХ УРАВНЕНИЙ С n НЕИЗВЕСТНЫМИ.
Квадратная матрица A называется невырожденной, если ее строки линейно независимы.
Согласно этому определению, свойствам определителей, критерию существования обратной матрицы получаем, что невырожденная матрица имеет ненулевой определитель и обладает обратной матрицей.
Благодаря этим свойствам имеем два особых метода решения системы A`x =` b с квадратной невырожденной матрицей A.
МАТРИЧНЫЙ МЕТОД РЕШЕНИЯ СЛУ.
ТЕОРЕМА.
Если матрица A системы A`x =` b квадратная невырожденная, то существует единственное решение`x * этой системы, равное произведению обратной матрицы A– 1 на столбец свободных членов` b, `x * = A– 1` b.
ДОКАЗАТЕЛЬСТВО.
Докажем сначала, что вектор`x * является решением системы A`x =` b. В самом деле, A`x * = A · A– 1` b = E` b = ` b, то есть A`x * =` b и`x * является решением системы A`x =` b.
Докажем теперь единственность этого решения. Предположим, что имеется еще другое решение`x 1, то есть A`x 1 =` b — верное равенство. Домножим обе части этого равенства слева на A– 1. Получим A– 1 A`x 1 = A– 1` b и, следовательно,`x 1 = A– 1` b, то есть`x 1 =`x *. Теорема доказана.
Таким образом, матричный метод решения системы A`x =` b с квадратной невырожденной матрицей A состоит в нахождении решения этой системы по формуле`x * = A– 1` b.
|
|
|
ПРАВИЛО КРАМЕРА.
ТЕОРЕМА.
Если матрица A системы A`x =` b квадратная невырожденная, то существует единственное решение`x * = 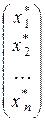 этой системы, которое может быть найдено по формулам:
этой системы, которое может быть найдено по формулам:
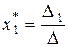 ,
, 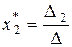 , …,
, …, 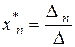 , где D — определитель матрицы A, D j — определитель, полученный из D заменой в нем j –го столбца на столбец свободных членов` b (для всех j = 1, 2, …, n).
, где D — определитель матрицы A, D j — определитель, полученный из D заменой в нем j –го столбца на столбец свободных членов` b (для всех j = 1, 2, …, n).
ПРИМЕР решения системы линейных уравнений по правилу Крамера.
 .
.
D = 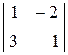 = 1 + 6 = 7, D 1 =
= 1 + 6 = 7, D 1 = 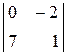 = 0 + 14 = 14, D 2 =
= 0 + 14 = 14, D 2 = 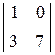 = 7 – 0 = 7,
= 7 – 0 = 7,
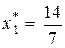 = 2,
= 2,  = 1,`x * =
= 1,`x * = 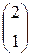 .
.
№ 15. ТЕОРЕМЫ КРОНЕКЕРА – КАПЕЛЛИ И ОБ ОПРЕДЕЛЁННОСТИ СЛУ. АЛГОРИТМ РЕШЕНИЯ СЛУ С ПОМОЩЬЮ ОЖИ.
ТЕОРЕМА КРОНЕКЕРА – КАПЕЛЛИ.
Для того, чтобы система уравнений A`x =` b была совместной, необходимо и достаточно, чтобы ранг матрицы этой системы равнялся рангу ее расширенной матрицы.
ДОКАЗАТЕЛЬСТВО.
1) Пусть система уравнений A`x =` b является совместной. Докажем, что ранг r A матрицы A равняется рангу r à расширенной матрицы Ã.
Представим матрицы A и Ã как системы их векторов столбцов
| `A 1,`A 2, …,`A n | (1) |
и
| `A 1, `A 2, …,`A n , ` b | (2) |
соответственно. Ранг матрицы A равен рангу системы векторов (1), а ранг матрицы Ã равен рангу системы векторов (2). Поскольку система векторов (1) является подсистемой системы векторов (2), то r A £ r Ã.
Так как система A`x =` b является совместной, то существует вектор `x * = 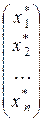 , координаты которого удовлетворяют данной системе, или, в векторном виде, имеет место равенство x 1*`A 1 + x 2*`A 2 + … + x n *`A n =` b. Отсюда следует, что` b Î L (`A 1,`A 2 , …,`A n) и, следовательно,
, координаты которого удовлетворяют данной системе, или, в векторном виде, имеет место равенство x 1*`A 1 + x 2*`A 2 + … + x n *`A n =` b. Отсюда следует, что` b Î L (`A 1,`A 2 , …,`A n) и, следовательно,
`A 1,`A 2 , …,`A n ,` b Î L (`A 1,`A 2 , …,`A n ). По свойствам ранга системы векторов r à £ r A. Но так как r A £ r Ã, то r A = r Ã.
2) Пусть теперь r A = r à = r. Докажем, что система A`x =` b является совместной. Согласно определению базиса системы векторов базисы систем (1) и (2) содержат по r векторов. Пусть`A 1, `A 2 , …,`A r — базис системы (1). Тогда эти же векторы будут являться и базисом системы (2). Действительно, векторы`A 1,`A 2 , …,`A r образуют линейно независимую подсистему системы (2), а поскольку их количество совпадает с рангом системы (2), то они являются базисом этой системы. Следовательно, вектор` b можно представить в виде линейной комбинации векторов`A 1,`A 2 , …,`A r:
` b = l 1`A 1 + l 2`A 2 + … + l r `A r, а также в виде линейной комбинации
` b = l 1`A 1 + l 2`A 2 + … + l r `A r + 0`A r + 1 + … + 0`A n. Справедливость последнего равенства означает, что вектор`x *, координатами которого являются числа l 1, l 2 , …, l r, 0, …, 0 является решением системы уравнений A`x =` b, то есть система A`x =` b совместна. Теорема доказана.
|
|
|
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 378; Нарушение авторских прав?; Мы поможем в написании вашей работы!