Алгоритм решения системы линейных уравнений

ТЕОРЕМА ОБ ОПРЕДЕЛЕННОСТИ СЛУ.

Пусть система уравнений A`x =` b является совместной, имеет n неизвестных и r _A = r _Ã = r.

Тогда если r = n, то система A`x =` b имеет единственное решение, если r < n, то система A`x =` b имеет бесконечно много решений.

Переменные, соответствующие линейно независимым столбцам матрицы A, называются базисными переменными. Количество базисных переменных равно r — рангу матрицы A

Остальные переменные системы линейных уравнений называются свободными, количество свободных переменных равно n – r.

Решение системы, в котором ненулевые значения имеют только базисные переменные, называется базисным решением.

В справедливости теоремы об определенности убедимся, рассмотрев алгоритм решения СЛУ с помощью ОЖИ.

Пусть дана система уравнений A`x =` b. Перепишем ее в табличном виде:

	x 1	x 2	…	x n
0 =	a 11	a 12	…	a 1 n	– b 1
0 =	a 21	a 22	…	a 2 n	– b 2
…	…	…	…	…	…
0 =	a m 1	a m 2	…	a m n	– b m

Столбцы под переменными образуют матрицу A, а все столбцы таблицы — расширенную матрицу Ã, ранги которых обозначим r _A и r _Ã соответственно.

Выполним максимально возможное число шагов ОЖИ, выбирая разрешающие элементы в столбцах под переменными.

Заметим, что столбец, являющийся разрешающим на некотором шаге ОЖИ, на последующих шагах разрешающим являться не может и, следовательно, не повлияет на величину остальных элементов таблицы. Его собственные элементы не представляют никакого интереса, так как при выполнении одного шага ОЖИ над столбцом, являвшимся разрешающим, вместо переменной x _s окажется 0.Поэтому рекомендуется на каждом шаге ОЖИ сокращать таблицу на разрешающий столбец.

Пересчет таблицы для системы A`x =` b означает реализацию обычного метода подстановки, а для матрицы A и расширенной матрицы этой системы — вычисление их рангов. Поскольку разрешающие элементы выбираются только в столбцах под переменными, пересчет будет закончен после выполнения r _A шагов ОЖИ. По окончании пересчета получим жорданову таблицу одного из следующих видов:

1. а) r _A = n.

x 1 =	b 1
…	…
x n =	b n
0 =

В этом случае r _A = n и r _Ã = n, так как выполнено n шагов ОЖИ, и больше нельзя сделать ни одного шага (у матрицы A все столбцы использованы, а у расширенной матрицы в неиспользованном столбце под 1 невозможно выбрать ненулевой разрешающий элемент в неиспользованной строке). Система совместна и имеет единственное решение, которое можно получить, выписав выражения для переменных из таблицы: x ₁ = b ₁, …, x _n = b _n, то есть `x ^*= .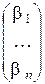

1.б) r _A = n.

x 1 =	b 1
…	…
x n =	b n
0 =	b ¹ 0

В этом случае r _A = n и r _Ã = n + 1, так как выполнено n шагов ОЖИ, у матрицы A все столбцы использованы, а у расширенной матрицы в неиспользованном столбце под 1 можно выбрать ненулевой разрешающий элемент b в неиспользованной строке. Система несовместна, так как r _A ¹ r _Ã.

2. а) r _A < n.

	x r +1	…	x n
x 1 =	b 1 r +1	…	b 1 n	b 1
…	…	…	…	…
x r =	b r r + 1	…	b r n	b r
0 =		…

В этом случае r _A = r и r _Ã = r, так как выполнено r шагов ОЖИ, и больше нельзя сделать ни одного шага (у матрицы A и у расширенной матрицы в неиспользованных столбцах невозможно выбрать ненулевой разрешающий элемент в неиспользованной строке). Так как r _A = r _Ã, то система уравнений совместна.

Переменные x ₁, …, x _r соответствуют линейно независимым столбцам матрицы A и являются базисными.

Переменные x _{r + 1}, …, x _n, оставшиеся наверху таблицы, являются свободными.

Для получения решений системы выпишем из таблицы соотношения между переменными: 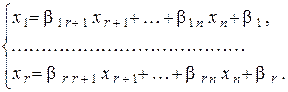. Придавая свободным переменным x _{r +1}, …, x _n, стоящим в правой части, произвольные значения, можно получить бесконечно много различных решений системы A`x =` b. Например, базисное решение системы имеет вид = .

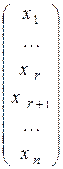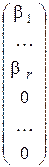2. б) r _A < n.

	x r +1	…	x n
x 1 =	b 1 r +1	…	b 1 n	b 1
…	…	…	…	…
x r =	b r r + 1	…	b r n	b r
0 =		…		b ¹ 0

В этом случае r _A = r и r _Ã = r + 1, так как выполнено r шагов ОЖИ, у матрицы A в неиспользованных столбцах невозможно выбрать ненулевой разрешающий элемент в неиспользованной строке, а у расширенной матрицы в столбце под 1 можно выбрать ненулевой разрешающий элемент b в неиспользованной строке и сделать еще один шаг ОЖИ.

Система несовместна, так как r _A ¹ r _Ã.

№ 16. ОДНОРОДНЫЕ СЛУ. ПРОСТРАНСТВО РЕШЕНИЙ.

Однородной системой линейных уравнений называется система вида A`x =`0.

Однородные системы всегда совместны, так как A`0 =`0 — верное равенство. Таким образом, если система A`x =`0 имеет единственное решение, то это`x <sup>*</sup> =`0. Если же однородная система имеет ненулевое решение, то в силу теоремы об определенности это означает, что она имеет бесконечно много решений.

ТЕОРЕМА.

Множество решений X ^* системы уравнений A`x =`0 с n неизвестными образует подпространство пространства R ⁿ.

ДОКАЗАТЕЛЬСТВО.

Проверим выполнение условий линейности из определения подпространства.

Возьмем векторы`x,`y Î X ^*. Докажем, что их сумма`x +`y Î X ^*.Так как`x,`y Î X ^*, то A`x =`0 и A`y =`0. Убедимся, что A (`x +`y) =`0. Действительно, A (`x +`y) = A`x + A`y =`0 +`0 =`0, то есть`x +`y Î X ^*.

Пусть теперь`x Î X <sup>*</sup>, l Î R. Докажем, что l`x Î X ^*. Так как A`x =`0, то A (l`x) = l (A`x) = l`0 =`0, то есть l`x Î X ^*.

Следовательно, X ^* является подпространством пространства R ⁿ.

Теорема доказана.

Множество решений однородной системы линейных уравнений называется пространством решений этой системы.

№ 17. Размерность пространства решений. Фундаментальная система решений и её построение. Общее решение однородной СЛУ.

Базис пространства решений называется фундаментальной системой решений. В дальнейшем мы увидим, что фундаментальная система решений содержит n – r векторов (n — количество неизвестных системы A`x =`0, r — ранг матрицы A), откуда следует, что dim X ^* = n – r.

Рассмотрим алгоритм построения фундаментальной системы решений.

Предположим, что при решении некоторой однородной системы уравнений методом ОЖИ мы получили итоговую таблицу

	x r +1	…	x n
x 1 =	b 1 r + 1	…	b 1 n
…	…	…	…
x r =	b r r + 1	…	b r n
0 =		…

Из свободных переменных x _{r + 1}, …, x _n составим вектор 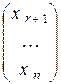, который принадлежит пространству R ^{n – r}. Построим n – r решений системы уравнений, придавая свободным переменным x _{r + 1}, …, x _n значения так, чтобы составленные из них векторы совпадали с векторами` e <sub>1</sub>,` e ₂ , …,` e _{n – r} — стандартным базисом пространства R ^{n – r}.

Пусть 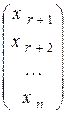=` e ₁ = .

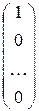Выпишем из таблицы соответствующие значения базисных переменных: x ₁ = b _{1 r + 1}, …, x _r = b _{r r + 1}. Решение`V <sub>1</sub>, соответствующее данному набору значений свободных переменных, имеет вид`V ₁ = .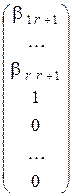

Для построения решения`V <sub>2</sub> возьмем = ` e ₂ = .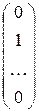

Выпишем из таблицы соответствующие значения базисных переменных: x ₁ = b _{1 r + 2}, …, x _r = b _{r r + 2}.

Следовательно, решение`V<sub>2</sub> имеет вид`V₂ = .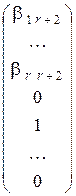

Продолжая процесс, для построения решения`V _{n – r} возьмем

=` e _n = 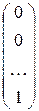. Соответствующие значения базисных переменных:

x ₁ = b _{1 n}, …, x _r = b _{r n}, `V _{n – r} = .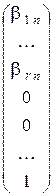

В итоге получили систему векторов`V <sub>1</sub> ,`V ₂ , …,`V _{n – r}, которая является фундаментальной системой решений, то есть базисом пространства решений нашей однородной системы уравнений.

Действительно, система векторов`V <sub>1</sub>,`V ₂ , …,`V <sub>n – r</sub> линейно независимая, так как из равенства l <sub>1</sub>`V ₁ + l ₂`V<sub>2</sub> + … + l <sub>n – r</sub> `V _{n – r} =`0 с очевидностью следует, что l ₁ = l ₂ = … = l _{n – r} = 0. (Проверьте!)

Кроме того, любое решение`x 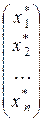<sup>*</sup> = можно представить в виде линейной комбинации векторов`V ₁,`V<sub>2</sub> , …,`V _{n – r}. В самом деле, из итоговой жордановой таблицы следует, что 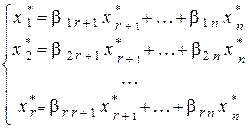, и, следовательно,`x 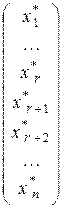^* = = x^*_{r + 1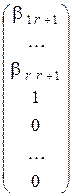} + x^*_{r + 2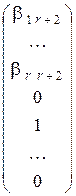} +… + x^*_n =

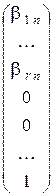= x^*_{r + 1}`V <sub>1</sub> + x<sup>*</sup><sub>r + 2</sub>`V ₂ + … + x^*_n `V _{n – r}.

Поскольку любое решение однородной системы линейных уравнений можно представить в виде линейной комбинации векторов фундаментальной системы решений, получаем формулу для общего решения`x _{o o} однородной системы:

`x <sub>o o</sub> = l <sub>1</sub>`V ₁ + l ₂`V <sub>2</sub> + … + l <sub>n – r</sub> `V _{n – r},

где`V <sub>1</sub>,`V ₂, …,`V _{n – r} — фундаментальная система решений, а

l ₁, l ₂, …, l _{n – r} — произвольные вещественные числа.

№ 18. Базисные и свободные переменные. Базисное решение. Теорема о связи решений неоднородной и соответствующей ей однородной СЛУ. Общее решение неоднородной СЛУ.

Пусть дана неоднородная система A` x =` b.	(1)
Рассмотрим наряду с ней однородную систему A` x =`0	(2)

с той же самой матрицей А. Между решениями систем (1) и (2) существует связь, определяемая следующими теоремами.

ТЕОРЕМА 1.

Сумма произвольного решения системы (1) и произвольного решения системы (2) является решением системы (1).

ДОКАЗАТЕЛЬСТВО.

Пусть` x <sub>1</sub> — решение системы (1), а` x ₀ — решение системы (2), то есть A` x <sub>1</sub> =` b, A` x <sub>0</sub> =`0. Рассмотрим вектор` x =` x ₁ +` x <sub>0</sub> . A` x = A (` x <sub>1</sub> +` x ₀ ) = = A` x <sub>1</sub> + A` x ₀ =` b +`0 =` b. Следовательно,` x является решением системы (1). Теорема доказана.

ТЕОРЕМА 2.

Разность любых двух решений системы (1) является решением системы (2).

ДОКАЗАТЕЛЬСТВО.

Пусть` x <sub>1</sub> и` x ₂ — произвольные решения системы (1), то есть

A` x <sub>1</sub> =` b, A` x <sub>2</sub> =` b. Рассмотрим вектор` x =` x ₁ –` x ₂ .

A` x = A (` x ₁ –` x <sub>2</sub> ) = A` x ₁ – A` x <sub>2</sub> =` b –` b =`0. Следовательно,` x является решением системы (2). Теорема доказана.

ТЕОРЕМА 3.

Пусть` x <sub>ч н</sub> — некоторое частное решение неоднородной системы A` x =` b.

Для того, чтобы вектор` x был решением системы A` x =` b необходимо и достаточно, чтобы вектор` x можно было представить в виде суммы

` x =` x _{ч н} +` x <sub>0</sub> , где`x ₀ — решение однородной системы A` x =`0.

ДОКАЗАТЕЛЬСТВО.

Если` x =` x _{ч н} +` x <sub>0</sub> , то по теореме (1) он является решением системы A` x =` b.

Обратно, если` x является решением системы A` x =` b, то, очевидно,

` x =` x _{ч н} + (` x –` x _{ч н}). По теореме (2) вектор`x <sub>0</sub> =` x –` x <sub>ч н</sub> является решением системы A` x =`0. Теорема доказана.

СЛЕДСТВИЕ.

Общее решение` x <sub>о н</sub> неоднородной системы A` x =` b имеет вид

` x <sub>о н</sub> =` x _{ч н} +` x _{о о}.

№ 19. Метод Гаусса решения СЛУ.

Идея метода Гаусса состоит в том, чтобы с помощью элементарных преобразований привести систему уравнений A` x =` b к равносильной ей системе A ₁` x =` b ₁, матрица которой имеет треугольный вид или вид трапеции.

Элементарными преобразованиями называются следующие преобразования системы уравнений:

– перестановка уравнений,

– изменение порядка следования переменных в уравнениях (сразу во всех и одинаково),

– умножение (деление) некоторого уравнения системы на отличное от нуля число,

– замена какого-либо уравнения системы на его сумму с другим уравнением, умноженным на произвольное число.

Заметим, что элементарные преобразования не меняют ранга матрицы системы (см. свойства ранга матрицы), поэтому ранги матриц A и A ₁ совпадают. Также совпадают ранги расширенных матриц Ã и Ã ₁ систем уравнений A` x =` b и A ₁` x =` b ₁ соответственно.

Применение метода Гаусса к решению систем линейных уравнений разного типа рассмотрим на примерах.

ПРИМЕР 1.

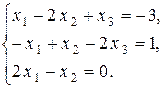
Первое уравнение, умноженное на 1 и на (– 2), прибавим ко второму и третьему уравнениям соответственно:

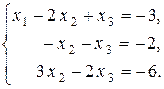
Второе уравнение, умноженное на 3, прибавим к третьему уравнению:

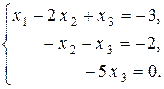
Матрица полученной системы уравнений имеет треугольный вид

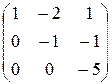, расширенная матрица 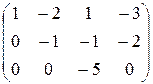имеет вид трапеции.

Их ранги равны числу ненулевых строк, то есть трем. Согласно теореме Кронекера – Капелли и теореме об определенности система совместна и имеет единственное решение. Найдем это решение. Из третьего уравнения следует, что x ₃ = 0. Тогда из второго уравнения получим, что – x ₂ = – 2, то есть x ₂ = 2. Подставляя полученные значения переменных x ₂ и x ₃ в первое уравнение, получим x ₁ – 4 + 0 = – 3, x ₁ = 4 – 3, x ₁ = 1.

Единственным решением системы уравнений 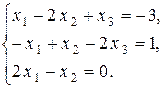является вектор`x = .

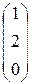ПРИМЕР 2.

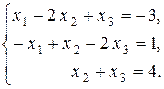
Первое уравнение, умноженное на 1, прибавим ко второму уравнению:

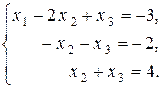
Второе уравнение прибавим к третьему уравнению:

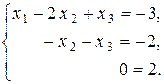
Матрица A ₁ полученной системы уравнений и ее расширенная матрица Ã ₁ имеют вид трапеции:

A ₁ = 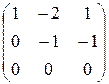, Ã ₁ = 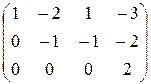. Их ранги равны числу ненулевых строк, то есть двум и трем соответственно. Согласно теореме Кронекера – Капелли система несовместна.

ПРИМЕР 3.

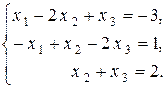
Первое уравнение, умноженное на 1, прибавим ко второму уравнению:

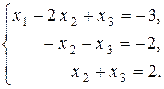
Второе уравнение прибавим к третьему уравнению:

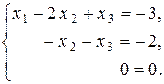
Матрица A ₁ полученной системы уравнений и ее расширенная матрица Ã ₁ имеют вид трапеции: A ₁ = 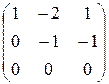, Ã ₁ = .

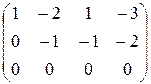Их ранги равны числу ненулевых строк, то есть двум. Согласно теореме Кронекера – Капелли и теореме об определенности система совместна и имеет бесконечно много решений.

Получим общее решение данной системы уравнений.

Поскольку` x <sub>о н</sub> =` x _{ч н} +` x _{о о} нам требуется построить частное решение системы 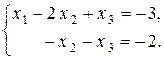и общее решение системы

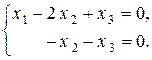
Заметим, что переменные x ₁ и x ₂ соответствуют линейно независимым столбцам матрицы A ₁ и, следовательно, являются базисными переменными. Переменная x ₃ является свободной. Выразим базисные переменные через свободную переменную:

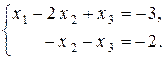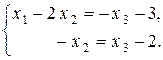Û Û Û

Û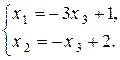

В качестве` x _{ч н} возьмем базисное решение, которое можно получить, придав свободной переменной x ₃ нулевое значение: x ₃ = 0. Тогда

x ₁ = 1, x ₂ = 2, ` x _{ч н} = .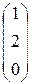

Из однородной системы 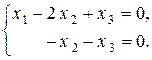получим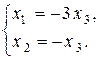

Поскольку размерность пространства решений однородной системы равна n – r = 3 – 2 = 1, фундаментальная система решений будет состоять только из одного вектора`V. Получим вектор`V, придав свободной переменной x ₃ значение, равное 1:

x ₃ = 1, x ₁ = – 3, x ₂ = – 1,`V = 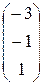,` x _{о о} = l .

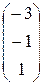` x _{о н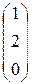} = + l .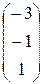

Дата добавления: 2015-04-24