Вопрос 4. Действия над матрицами: свойства операций

Действия над матрицами: свойства операций.

Основные действия над матрицами:

При сложении и вычитании матрицы должны быть одного размера.
Операция умножения(деления) матрицы любого размера на любое число сводится к умножению(делению) каждого элемента матрицы на это число.

Сложение матриц: А+В=В+А; α(А+В)= αА+ αВ

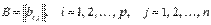Суммой двух матриц и является матрица, элементы которой равны сумме соответствующих элементов матриц А и В, то есть, .

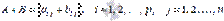Таким образом, результатом сложения двух матриц является матрица того же порядка.
Свойства операции сложения матриц.
1.Для матриц А, В и С одного порядка характерно свойство ассоциативности сложения А + (В + С) = (А + В) + С.

2.Для матриц данного порядка существует нейтральный элемент по сложению, которым является нулевая матрица. То есть, справедливо свойство А + О = А.

3.Для ненулевой матрицы А данного порядка существует матрица (– А), их суммой является нулевая матрица: А + (- А) = О.

4.Для матриц А и В данного порядка справедливо свойство коммутативности сложения А + В = В + А.

Операция умножения матриц.
Произведением матриц называется матрица, элементы которой могут быть вычислены по формуле:

Свойства операций умножения матриц.
Чтобы найти элемент первой строки и первого столбца необходимо каждый элемент первой строки матрицы А умножить на соответствующий элемент первого столбца матрицы В и полученные результаты сложить.
1) Умножение матриц не коммуникативно
А*В не равно В*А
Матрица А умножить на единичную матрицу Е = матрица А
Матрица А умножить на нулевую матрицу О=0
2)Операция перемножения матриц ассоциативна
А*(В*С)=(А*В)*С

3)Операция умножения матриц дистрибутивна по отношению к сложению.
А*(В+С)=А*В+А*С
4)Если произведение А*В определено, то для любого числа α верно соотношение
α (А*В)=(α *А)*В=А*(α *В)

5)Если определено произведение матриц А*В, то определено произведение В^Т *А^Т

(А*В) ^Т = В^Т *А^Т , где индексом Т определена транспонированная матрица.
Матрица В называется транспонированной матрице А, а переход от А к В –транспонированием, если элемент каждой строки матрицы А записать в том же порядке в столбцы матрицы В.
Операция умножения двух матриц.
Операция умножения двух матриц А и В определена, когда ЧИСЛО СТОЛБЦОВ МАТРИЦЫ А РАВНО ЧИСЛУ СТРОК МАТРИЦЫ В.
Произведением матрицы А порядка на матрицу В порядка 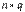является такая матрица С порядка , каждый элемент которой равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-ого столбца матрицы В, то есть,

Таким образом, результатом умножения матрицы порядка 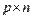на матрицу порядка 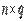является матрица порядка .

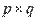Вопрос 5.
Обратная матрица: определение, теорема о существовании.

Если А – квадратная матрица, то обратной по отношению к ней называется матрица, которая будучи умноженной на А как справа, так и слева дает единичную матрицу.
А^-1 *А=А* А^-1 =Е

Только квадратная матрица имеет обратную матрицу.
Если обратная матрица А^-1 существует, то матрица А называется обратимой.

Операция вычисления обратной матрицы называется обращением матрицы.

Теорема: Для того, чтобы квадратная матрица А имела обратную матрицу необходимо и достаточно, чтобы матрица была вырожденной, т.е модуль А не равен нулю.
Алгоритм вычисления обратной матрицы:

1)Находят определитель матрицы А

2)Находят алгебраические дополнения всех элементов матрицы А и записывают новую матрицу.

3)Транспонируют полученную матрицу.

4)Умножают полученную матрицу на 1/модуль А

Пример: Дана матрица 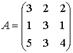. Найти обратную матрицу.

Р е ш е н и е: Вычисляем определитель матрицы A:

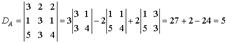
Находим алгебраические дополнения элементов этого определителя:

, ,
, ,

, ,

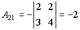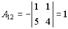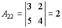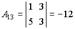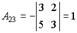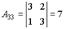
Следовательно,

Вопрос 6.

Нахождение обратной матрицы методом Жордана-Гаусса.

Метод Гаусса — Жордана (метод полного исключения неизвестных) — метод, который используется для решения квадратных систем линейных алгебраических уравнений, нахождения обратной матрицы, нахождения координат вектора в заданном базисе или отыскания ранга матрицы.

Алгоритм:

1. Выбирают первый слева столбец матрицы, в котором есть хоть одно отличное от нуля значение.

2. Если самое верхнее число в этом столбце есть ноль, то меняют всю первую строку матрицы с другой строкой матрицы, где в этой колонке нет нуля.

3. Все элементы первой строки делят на верхний элемент выбранного столбца.

4. Из оставшихся строк вычитают первую строку, умноженную на первый элемент соответствующей строки, с целью получить первым элементом каждой строки (кроме первой) ноль.

5. Далее проводят такую же процедуру с матрицей, получающейся из исходной матрицы после вычёркивания первой строки и первого столбца.

6. После повторения этой процедуры 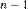раз получают верхнюю треугольную матрицу

7. Вычитаем из предпоследней строки последнюю строку, умноженную на соответствующий коэффициент, с тем, чтобы в предпоследней строке осталась только 1 на главной диагонали.

8. Повторяют предыдущий шаг для последующих строк. В итоге получают единичную матрицу и решение на месте свободного вектора (с ним необходимо проводить все те же преобразования).

9. Чтобы получить обратную матрицу, нужно применить все операции в том же порядке к единичной матрице.

Пример:

Для решения следующей системы уравнений:

Запишем её в виде матрицы 3×4, где последний столбец является свободным членом:

Проведём следующие действия:

§ К строке 2 добавим: −4 × Строку 1.

§ К строке 3 добавим: −9 × Строку 1.

Получим:

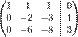
§ К строке 3 добавим: −3 × Строку 2.

§ Строку 2 делим на −2

§ К строке 1 добавим: −1 × Строку 3.

§ К строке 2 добавим: −3/2 × Строку 3.

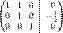
§ К строке 1 добавим: −1 × Строку 2.

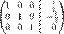
В правом столбце получаем решение:

.

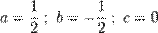Дата добавления: 2015-04-24