Необходимое условие интегрируемости функции

Если функция f (x) интегрируема на отрезке [ a, b ], то она ограничена на этом отрезке.
Доказательство. Предположим обратное. Допустим, что f (x) является неограниченной на отрезке [ a, b ]. Покажем, что в этом случае интегральную сумму можно сделать сколь угодно большой за счет выбора точек ξ ₁, ξ ₂,…, ξ _n при любом разбиении отрезка [ a, b ].
Действительно, так как f (x) не ограничена на [ a, b ], то при любом разбиении отрезка [ a, b ] она обладает этим свойством хотя бы на одном частичном отрезке разбиения, например на [ x ₀, x ₁]. Выберем на остальных частях отрезка точки ξ ₂, ξ ₃,…, ξ _n произвольно и обозначим

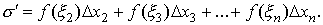
Зададим произвольное число М > 0 и возьмем такое ξ ₁ на [ x ₀, x ₁], чтобы

.

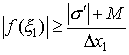Это можно сделать в силу неограниченности функции f (x) на [ x ₀, x ₁]. Тогда

и ,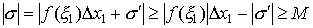

т.е. интегральная сумма σ по абсолютной величине может быть больше любого наперед заданного числа. Поэтому интегральная сумма σ не имеет конечного предела при λ → 0, а это означает, что определенный интеграл от неограниченной функции не существует.
Замечание. Обратная теорема неверна, т.е. условие ограниченности функции f (x) необходимое, но не является достаточным условием интегрируемости функции. Поясним это утверждение примером. Рассмотрим функцию Дирихле на отрезке [0,1]:

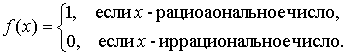
Функция Дирихле, очевидно, ограниченна. Однако она не интегрируема на [0,1]. Действительно, если при любом разбиении отрезка [0,1] выбрать рациональные точки ξ _i (x _{i - 1} ≤ ξ _i ≤ x _i), то получим

,

а если взять ξ _i иррациональным, то получим

.

Таким образом, при разбиении на сколь угодно малые частичные отрезки интегральная сумма может принимать как значение, равное 0, так и значение, равное 1. Поэтому интегральная сумма σ при λ → 0 предела не имеет.
Для существования определенного интеграла от некоторой функции f (x) последняя, помимо ограниченности, должна обладать дополнительными свойствами, обеспечивающими ее интегрируемость. Для установления этих свойств необходимо ввести понятия нижних и верхних сумм.

Дата добавления: 2015-04-24