Методы решения 2 страница

1) ,

2) при и при .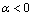

Очевидно, что при .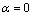

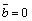Построим, например, векторы и для заданного вектора 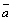(рис. 6).

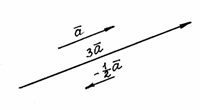
Рис. 6

Из определения следует: два вектора 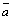и коллинеарны тогда и только тогда, когда имеет место равенство :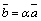

(2.1)

Свойства линейных операций:

1) ;

2) ;

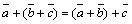3) ; ;

4) ;

5) ;

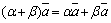6) ;

7) ; ;

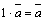Пусть дан вектор 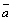. Ортом вектора 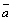(обозначается 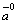) называется вектор единичной длины, сонаправленный с вектором .

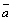Очевидно, 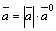для любого вектора .

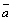16. Простейшие задачи аналитической геометрии (расстояние между точками, деление отрезка в заданном отношении).

Рассмотрим точки A ₁ (x ₁; y ₁; z ₁) и A ₂ (x ₂; y ₂; z ₂) и найдем расстояние между этими точками. Пусть вначале прямая A ₁ A ₂ не параллельна оси z (чертеж 9.4.1).

Проведем через точк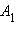и и прямые, параллельные оси z. Пусть эти прямые пересекут плоскость xy в точках 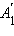и Заметим, что поскольку эти точки лежат в плоскости xy, то координата z у них равна нулю. Проведем плоскость через точку 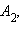параллельную плоскости xy. Пусть эта плоскость пересекает прямую 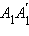в точке C. Применим теорему Пифагора к треугольнику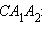 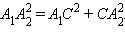Очевидно, что отрезки и 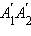равны, а согласно теореме Пифагора на плоскости xy, получаем, что Поскольку длина отрезк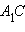а равна то окончательно имеем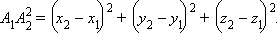

Если же окажется, что отрезок 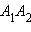параллелен оси z, то Но тот же результат дает полученная формула, так как в этом случае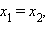

Итак, доказана следующая

Теорема 9.7.

Расстояние между точками A ₁ и A ₂ можно вычислить по формуле

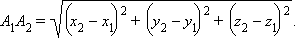
Определение 9.14.

Вектор, конец которого совпадает с данной точкой, называется радиус-вектором данной точки.

Рассмотрим некоторую точку M в пространстве с координатами (x; y; z). Пусть M ₁, M ₂, M ₃ – точки пересечения с осями координат плоскостей, проходящих через точку M перпендикулярно к этим осям (чертеж 9.4.2). Тогда

По определению координаты точки M Значит, Совершенно аналогично Получается, что Тем самым доказана следующая

Теорема 9.8.

Координаты любой точки равны соответствующим координатам ее радиус-вектора.

Рассмотрим теперь две точк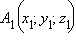и и 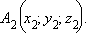По только что доказанному, 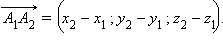Итак, каждая координата вектора равна разности соответствующих координат его конца и начала. Но длина вектора 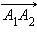по определению равна длине отрезка 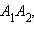а длина этого отрезка есть расстояние между точкам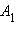и и Значит,

Эта формула позволяет вычислять длину вектора, зная его координаты.

ДЕЛЕНИЕ ОТРЕЗКА

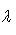
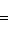
1. Если x1 и y1 - координаты точки A, а x2 и y2 - координаты точки B, то координаты x и y точки C, делящей отрезок AB в отношении 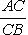, определяются по формулам

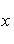
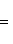
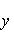
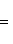
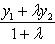
Если 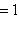, то точка C(x, y) делит отрезок AB пополам, и тогда координаты x и y середины отрезка AB определяются по формулам

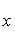
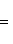
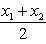
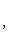
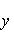
17. Общее уравнение прямой на плоскости, его частные случаи.

Общее уравнение
Ax + By + C = 0

Вектор = (А; В) - нормальный вектор прямой.

Частные случаи:

1) By + C = 0 - прямая параллельна оси Ox;

2) Ax + C = 0 - прямая параллельна оси Oy;

3) Ax + By = 0 - прямая проходит через начало координат;

4) y = 0 - ось Ox;

5) x = 0 - ось Oy.
Уравнение прямой в отрезках

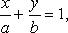
где a, b - величины отрезков, отсекаемых прямой на осях координат.
Нормальное уравнение прямой (рис. 4.11)

где 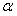- угол, образуемый нормально к прямой и осью Ox; p - расстояние от начала координат до прямой.

Приведение общего уравнения прямой к нормальному виду:

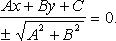
Здесь 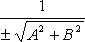- нормируемый множитель прямой; знак выбирается противоположным знаку C, если 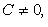и произвольно, если C = 0.

18. Угловой коэффициент прямой.

Угловой коэффициент прямой — коэффициент 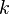в уравнении 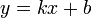прямой на координатной плоскости, численно равен тангенсу угла (составляющего наименьший поворот от оси Ox к оси Оу) между положительным направлением оси абсцисс и данной прямой линией.^[1]

Тангенс угла может рассчитываться как отношение противолежащего катета к прилежащему. k всегда равен 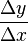, то есть производной уравнения прямой по x.

При положительных значениях углового коэффициента k и нулевом значении коэффициента сдвига b прямая будет лежать в первом и третьем квадрантах (в которых x и y одновременно положительны и отрицательны). При этом большим значениям углового коэффициента k будет соответствовать более крутая прямая, а меньшим — более пологая.

Прямые и 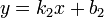перпендикулярны, если , а параллельны при

19. Уравнение прямой, проходящей через две заданные точки.

Прежде чем получить уравнение прямой, проходящей через две заданные точки в прямоугольной системе координат на плоскости, вспомним некоторые факты.

Одна из аксиом геометрии гласит, что через две несовпадающие точки на плоскости можно провести единственную прямую. Другими словами, задав две точки на плоскости, мы однозначно определяем прямую линию, которая через эти две точки проходит (при необходимости обращайтесь к разделу способы задания прямой на плоскости).

Пусть на плоскости зафиксирована прямоугольная декартова система координат Oxy. В этой системе координат любой прямой линии соответствует некоторое уравнение прямой на плоскости. С этой же прямой неразрывно связан направляющий вектор прямой. Этих знаний вполне достаточно, чтобы составить уравнение прямой, проходящей через две заданные точки.

Сформулируем условие задачи: составить уравнение прямой a, которая в прямоугольной декартовой системе координат Oxy проходит через две несовпадающие точки и .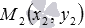

Покажем самое простое и универсальное решение этой задачи.

Нам известно, что каноническое уравнение прямой на плоскости вида 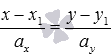задает в прямоугольной системе координат Oxy прямую линию, проходящую через точку и имеющую направляющий вектор .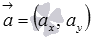

Напишем каноническое уравнение прямой a, проходящей через две заданные точки и .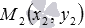

Очевидно, направляющим вектором прямой a, которая проходит через точки М1 и М2, является вектор 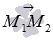, он имеет координаты (при необходимости смотрите статьювычисление координат вектора по координатам точек его конца и начала). Таким образом, мы имеем все необходимые данные, чтобы написать каноническое уравнение прямой a – координаты ее направляющего вектора и координаты лежащей на ней точки (и 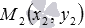). Оно имеет вид 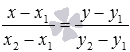(или ).

20. Уравнение прямой, проходящей через заданную точку в заданном направлении.

Предположим, что прямая проходит через точку M ₁ (x ₁, y ₁) и образует с осью OX угол j. Составим уравнение этой прямой.

Будем искать уравнение прямой в виде уравнения с угловым коэффициентом: y = k · x + b. Угловой коэффициент прямой можно найти, зная угол наклона k = tg j. Возьмем произвольную точку M (x, y), лежащую на этой прямой, и найдем уравнение, связывающее переменные x и y. Так как точки М и M ₁ лежат на прямой, то их координаты удовлетворяют уравнению прямой:

y = k · x + b,

y ₁ = k · x ₁ + b.

Вычитая эти равенства, получим:

y - y ₁ = k · (x - x ₁) - уравнение прямой, проходящей через данную точку в данном направлении.

21. Уравнение прямой с угловым коэффициентом.

Прямоугольная система координат позволяет задавать различные линии на плоскости их уравнениями.
Уравнением линии на плоскости в прямоугольной системе координат хОу называется уравнение f(х,у)=0, которому удовлетворяют координаты каждой точки данной линии и не удовлетворяют координаты любой точки плоскости, не лежащей на этой линии.

Пусть прямая l не параллельна оси Оу (рис.1). Обозначим точку пересечения прямой l с осью Оу буквой В(О;в), а угол между положительным направлением оси Ох и прямой l обозначим угол, отсчитываемый от оси Ох против часовой стрелки (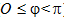), называется углом наклона прямой l к оси Ох.

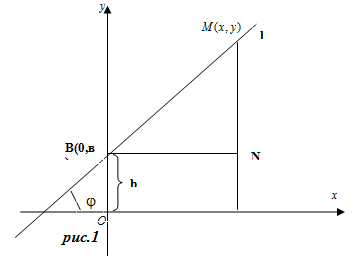
Выведем уравнение прямой l.
Пусть М(х,у) – произвольная точка прямой l с текущими координатами х,у. Из прямоугольного треугольника ВМN (рис.1) имеем:

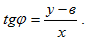(1)

Отсюда y-в=xtgφ, или у=xtgφ+в и окончательно

y=kx+в (2)

где k=tgφ - Тангенс угла наклона прямой к оси Ох называется угловым коэффициентом прямой.
Уравнение (2) называется уравнением прямой с угловым коэффициентом.
Число в – это величина отрезка, отсекаемого прямой на оси ординат.

22. Уравнение прямой в отрезках на осях.

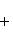
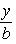
(3)

где a - величина отрезка, отсекаемого прямой на оси Ox; b - величина отрезка, отсекаемого прямой на оси Oy.

23. Угол между прямыми на плоскости, условия перпендикулярности и параллельности прямых.

Если уравнения прямой заданы в общем виде

A ₁ x + B ₁ y + C ₁ = 0,

A ₂ x + B ₂ y + C ₂ = 0, (6)

угол между ними определяется по формуле

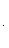(7)

4. Условия параллельности двух прямых:

а) Если прямые заданы уравнениями (4) с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов:

k ₁ = k ₂. (8)

б) Для случая, когда прямые заданы уравнениями в общем виде (6), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.

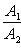
(9)

5. Условия перпендикулярности двух прямых:

а) В случае, когда прямые заданы уравнениями (4) с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.

(10)

24. Расстояние от точки до прямой на плоскости.

Расстояние от точки до прямой — равно длине перпендикуляра, опущенного из точки на прямую.

Если задано уравнение прямой Ax + By + C = 0, то расстояние от точки M(M_x, M_y) до прямой можно найти, используя следующую формулу

d =	|A·Mx + B·My+ C|
√(A^2 + B^2)

Дата добавления: 2015-04-24