Частные случаи

Шаг дискретизации примем постоянным: .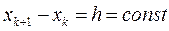

Формулы численного дифференцирования точные для многочленов второго порядка. Число узлов интерполяции для многочлена второго порядка равно трем.

Примем эти узлы равными: .

Схема интерполяции:

Оценку интерполяции производим в точке, совпадающей с началом координат:

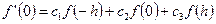
Рассмотрим равноотстоящую систему узлов:

Формулы вычисления второй производной, точной для многочлена второго порядка:

Получим систему уравнений, используя формулу для второй производной:

Получим формулу оценки производной в начале координат:

На практике часто используется несимметричная формула для производных:

I. 1)

2)

II. 1)

2)

Оценка производной берется в самой точке и в предшествующих точках:

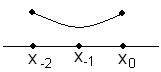
Существуют также формы для оценивания производных, расположенных между узлами интерполяции.

Несимметричные формулы для производных используются при численном решении дифференциальных уравнений.

Для этого все производные в дифференциальном уравнении выражаются через значение функции в соответствующих узлах интерполяции.

19. Квадратурные формулы Ньютона – Котеса.

Квадратурные формулы Ньютона-Котеса – большая группа формул, основанных на интерполяции подынтегральных функций.

Пусть – множество точек принадлежащих интервалу интегрирования .

С помощью этого множества задаются узлы интерполяции: , расположенные на интервале интегрирования . По указанным узлам интерполяции строится интегральный многочлен:

Интеграл заменяется приближенным интегралом: .

Ошибка численного интегрирования:

Из теории известно, что

– фиксированный многочлен

При этом квадратурная формула записывается в виде:

Формула, полученная методом интерполяции зависит от того, является ли число узлов четным или нечетным, а также зависит от формы весовой функции, которая может введена в эти уравнения.

Дата добавления: 2015-04-24