Алгоритм QR-разложения. Ортогональные матрицы и матрицы плоского вращения

Задача наименьших квадратов. Решение методом QR-разложения.

Задача наименьших квадратов, возникающая при научных и инженерных расчетах, может рассматриваться, как задача восстановления зависимости по эмпирическим данным.

Эмпирические данные представляют собой значения неизвестной функции, полученные в результате эксперимента на сетке узлов, в общем случае, неравномерной.

Узлы сетки могут представлять собой моменты времени или пространственные координаты линейной электрической или механической системы.

Координаты узлов и значения функции в этих узлах объединяются в набор точек 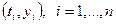, где 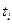– координаты узлов, 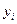– значения функции.

Задача заключается в определении коэффициентов аппроксимирующей функции, которая должна приближать наблюдаемые данные с возможно большей точностью.

Пример: 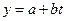. Такая функция часто используется при отслеживании дрейфа временных рядов в экономике.

В общем случае такая функция может не обеспечить требуемую точность восстановления зависимости. Поэтому в качестве аппроксимирующих функций используются общие многочлены по системе линейно-независимых функций:

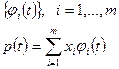
Система независимых функций, которая называется системой, может быть представлена в виде степенных функций, тригонометрических функций и др.

В случае степенных функций .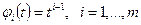

Число базисных функций и размерность пространства базисных функций, как правило, меняет число наблюдаемых данных.

В идеале, желательно, что бы ошибки в узлах сетки имели минимальную величину: .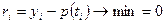

Если потребовать, чтобы ошибки в узлах сетки были равны нулю, то коэффициенты обобщенного многочлена должны удовлетворять матричному уравнению:

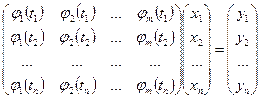
Решения этой системы возможно только при условии, если 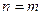, и определитель матрицы 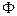отличен от нуля: 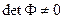, в противном случае решение этой системы оказывается невозможным. Однако, можно подобрать такие значения коэффициентов многочлена, чтобы полученный многочлен приближал наблюдаемые данные к значениям функции.

Точность восстановления зависимости, представленной вектором невязок 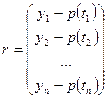можно представить некоторой нормой, которая характеризует среднее значение ошибок по всем узлам.

В качестве нормы можно использовать выражение:

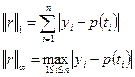
Евклидова норма: 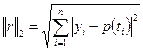или квадрат этой нормы: .

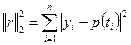Задача наименьших квадратов возникает из задачи минимизации квадрата евклидовой нормы

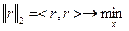
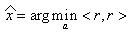
) Ортогональное преобразование любого вектора не изменяет его длины (евклидова норма):

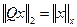
2) Ортогональное преобразование не изменяет углов между векторами в n-мерном пространстве.

Угол между векторами в n-мерном пространстве:

Для того, чтобы выражение имело смысл необходимо, чтобы его правая часть не превышала по модулю 1.

Это следует из неравенства Коши-Шварца:

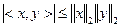
Сохранение углов между векторами следует из равенства:

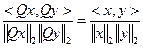
QR-разложение может быть осуществлено методами вращения и отражения.

Рассмотрим вращение вектора 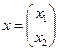на плоскости.

Матрица вращения задается в виде: 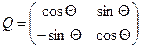, 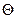– угол вращения.

Свойство ортогональной матрицы – сохранение угла между векторами.

Видно, что матрица вращения – ортогональная матрица:

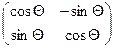
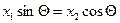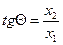Если принять, что или , то .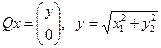

Рассмотрим систему линейных алгебраических уравнений второго порядка:

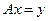
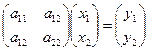
Найдем матрицу Q такую, что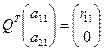

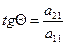
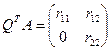, где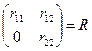

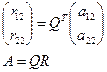
Рассмотрим систему уравнений с матрицей .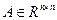

Плоской матрицей вращения называется матрица, имеющая вид:

Можно подтвердить, что матица Q является ортогональной матрицей с определителем, равным 1.

Применение указанной матрицы к i-му столбцу матрицы A: 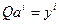, дает вектор 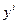, имеющий в j-ой позиции 0. (Верхний индекс обозначает номер вектора).

Применяя к исходной матрице указанные плоские матрицы вращения получим матрицу:

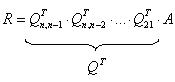
С помощью указанных матриц вращения все элементы матрицы R ниже главной диагонали становятся равными нулю.

Для исключения соответствующих элементов, коэффициенты c и s определяются выражениями:

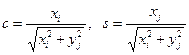
Произведение ортогональных матриц является ортогональной матрицей.

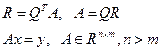
Чтобы решить задачу, матрица A дополняется матрицей 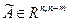, матрица A является произвольной.

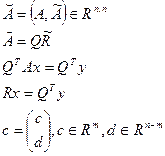
Учитывая, что ортогональное преобразование вектора невязки:

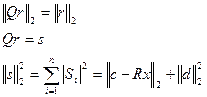
второе слагаемое не зависит от коэффициентов многочлена, линейное значение первого слагаемого сводится к решению системы уравнений: 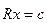, где R – верхняя треугольная матрица.

Решение задачи наименьших квадратов при 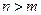, сводится к задаче решения системы алгебраических уравнений с верхней треугольной матрицей:

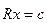
Чтобы применить метод QR-разложения к решению задачи наименьших квадратов, нужно привести матрицу A к квадратной форме:

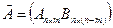
матрица B – произвольная.

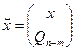
Исходное уравнение: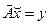

Матрица 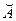является квадратной 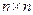. К этой системе можно применить метод QR-разложения.

Применяя метод вращения, уравнение записывается: ,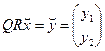

размерность вектора , размерность вектора ,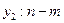

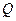– ортогональная матрица, 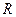– верхняя треугольная матрица.

Разобьем матрицу R на блоки:

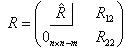
Умножая матрицу R справа на 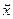можем записать:

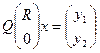
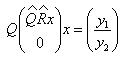
невязка (ошибка)

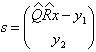
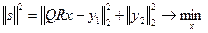
От неизвестных параметров зависит только первое слагаемое нормы невязки.

Минимальное значение этого слагаемого, если матрица A максимальный размер, определяется из уравнения: .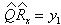

Таким образом, задача наименьших квадратов решается в два этапа.

На первом этапе осуществляется QR-разложение расширенной матрицы и определяются ее подматрицы 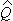и .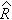

На втором этапе решается задача решения системы линейных алгебраических уравнений, матрица которой представлена в QR форме.

Матрица Q является ортогональной матрицей, т.е. матрицей, транспонирование которой совпадает с обратной матрицей.

Матрица R – верхняя треугольная матрица, решение которой осуществляется методом обратной подстановки.

модулю 1.

Это следует из неравенства Коши-Шварца:

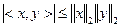
Сохранение углов между векторами следует из равенства:

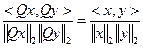
QR-разложение может быть осуществлено методами вращения и отражения.

Рассмотрим вращение вектора 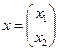на плоскости.

Матрица вращения задается в виде: 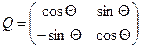, 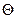– угол вращения.

Свойство ортогональной матрицы – сохранение угла между векторами.

Видно, что матрица вращения – ортогональная матрица:

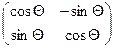
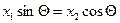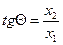Если принять, что или , то .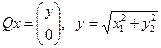

Рассмотрим систему линейных алгебраических уравнений второго порядка:

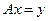
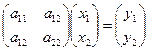
Найдем матрицу Q такую, что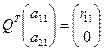

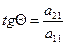
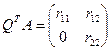, где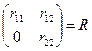

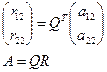
Рассмотрим систему уравнений с матрицей .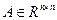

Плоской матрицей вращения называется матрица, имеющая вид:

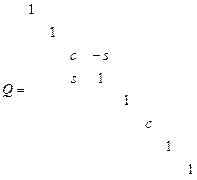
Можно подтвердить, что матица Q является ортогональной матрицей с определителем, равным 1.

Применение указанной матрицы к i-му столбцу матрицы A: 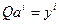, дает вектор 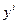, имеющий в j-ой позиции 0. (Верхний индекс обозначает номер вектора).

Применяя к исходной матрице указанные плоские матрицы вращения получим матрицу:

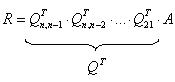
С помощью указанных матриц вращения все элементы матрицы R ниже главной диагонали становятся равными нулю.

Для исключения соответствующих элементов, коэффициенты c и s определяются выражениями:

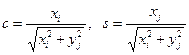
Произведение ортогональных матриц является ортогональной матрицей.

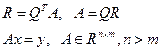
Чтобы решить задачу, матрица A дополняется матрицей 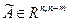, матрица A является произвольной.

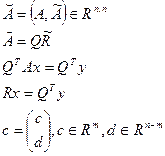
Учитывая, что ортогональное преобразование вектора невязки:

второе слагаемое не зависит от коэффициентов многочлена, линейное значение первого слагаемого сводится к решению системы уравнений: 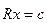, где R – верхняя треугольная матрица.

Решение задачи наименьших квадратов при 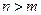, сводится к задаче решения системы алгебраических уравнений с верхней треугольной матрицей:

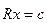
Чтобы применить метод QR-разложения к решению задачи наименьших квадратов, нужно привести матрицу A к квадратной форме:

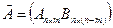
матрица B – произвольная.

Исходное уравнение: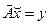

Матрица 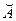является квадратной 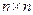. К этой системе можно применить метод QR-разложения.

Применяя метод вращения, уравнение записывается: ,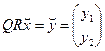

размерность вектора , размерность вектора ,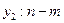

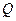– ортогональная матрица, 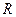– верхняя треугольная матрица.

Разобьем матрицу R на блоки:

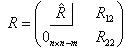
Умножая матрицу R справа на 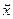можем записать:

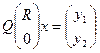
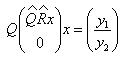
невязка (ошибка)

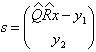
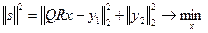
От неизвестных параметров зависит только первое слагаемое нормы невязки.

Минимальное значение этого слагаемого, если матрица A максимальный размер, определяется из уравнения: .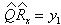

Таким образом, задача наименьших квадратов решается в два этапа.

На первом этапе осуществляется QR-разложение расширенной матрицы и определяются ее подматрицы 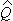и .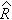

На втором этапе решается задача решения системы линейных алгебраических уравнений, матрица которой представлена в QR форме.

Матрица Q является ортогональной матрицей, т.е. матрицей, транспонирование которой совпадает с обратной матрицей.

Матрица R – верхняя треугольная матрица, решение которой осуществляется методом обратной подстановки.

Дата добавления: 2015-04-24