Решение задачи Коши с помощью формулы Тейлора

Задача численного решения обыкновенных дифференциальных уравнений. Задача Коши и граничные задачи.

Рассмотрим решение обыкновенного дифференциального уравнения первого порядка:

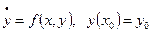
Существуют граничные задачи, в которых исходное решение или его производные должны принимать заданные значения на границах интервала.

Решение дифференциального уравнения ищется на интервале:

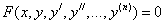, где x – независимая переменная, 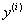- i-ая производная от искомой функции. n - порядок уравнения. Общее решение ОДУ n–го порядка содержит n произвольных постоянных , т.е. общее решение имеет вид .

Для выделения единственного решения необходимо задать n дополнительных условий. В зависимости от способа задания дополнительных условий существуют два различных типа задач: задача Коши и краевая задача. Если дополнительные условия задаются в одной точке, то такая задача называется задачей Коши. Дополнительные условия в задаче Коши называются начальными условиями. Если же дополнительные условия задаются в более чем одной точке, т.е. при различных значениях независимой переменной, то такая задача называется краевой. Сами дополнительные условия называются краевыми или граничными.

Ясно, что при n=1 можно говорить только о задачи Коши.

Примеры постановки задачи Коши:

Примеры краевых задач:

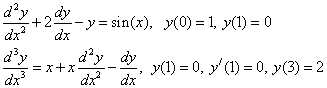
Решить такие задачи аналитически удается лишь для некоторых специальных типов уравнений.

Численные методы решения задачи Коши для ОДУ первого порядка

Постановка задачи. Найти решение ОДУ первого порядка

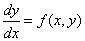на отрезке при условии

При нахождении приближенного решения будем считать, что вычисления проводятся с расчетным шагом , расчетными узлами служат точки промежутка [x0, xn].

Целью является построение таблицы

xi	x0	x1	…	xn
yi	y0	y1	…	yn

т.е. ищутся приближенные значения y в узлах сетки.

Интегрируя уравнение на отрезке , получим

Вполне естественным (но не единственным) путем получения численного решения является замена в нем интеграла какой–либо квадратурной формулой численного интегрирования. Если воспользоваться простейшей формулой левых прямоугольников первого порядка

,

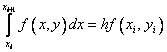Чтобы построить ряд Тейлора в окрестности точки, нужно найти значения производных функции в этих точках:

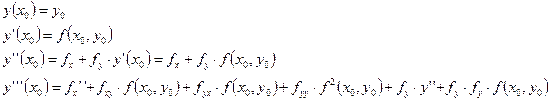и т.д.

В результате решения на интервале можно представить в виде конечного числа слагаемых ряда Тейлора: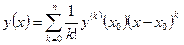

Недостаток этого метода:

необходимость вычисления для каждого дифференциального уравнения значений производных в начале интервала интегрирования.

Большую группу методов, свободную от этих недостатков, образуют методы Рунга-Кутта. К этим методам относятся методы Эйлера и Адама.

Метод Эйлера представляет собой аппроксимации производной разделенной разностью первого порядка.

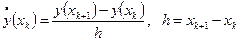Отсюда получим разностное уравнение:

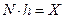– интервал интегрирования дифференциального уравнения.

Уравнение Эйлера и формулы Адамса определяется посредством приближения интеграла в интегральном уравнении, эквивалентном дифференциальному уравнению, с помощью соответствующих квадратурных формул.

Дифференциальное уравнение 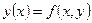может быть представлено эквивалентным интегральным уравнением:

Задача заключается в построении квадратурной формулы для этого интервала.

Простейшая формула – формула прямоугольника.

Формула прямоугольника на интервале 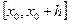может быть записана в виде:

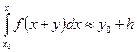
В этом случае имеет место формула Эйлера.

Точность формулы Эйлера имеет величину, пропорциональную квадрату шага дискретизации.

Более точная формула получится с помощью формулы трапеции:

Тогда расчетная формула принимает вид:

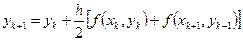Эта формула является нелинейной по искомому значению функции в конце интервала.

Точность этой формулы имеет величину второго порядка .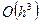

На практике, чтобы преодолеть эту сложность, значение в конце интервала в правой части уравнения заменяется на значение функции по формуле Эйлера. При этом, алгоритм решения задачи принимает вид:

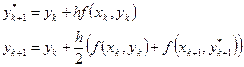
цикл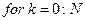

Второй подход к решению этой проблемы основывается на итерациях по значению функции в конце интервалов.

Алгоритм записывается:

цикл

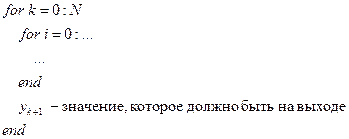
На практике: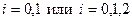

Аналогичным образом строится формула Адамса, основывается на методе Рунга-Кутта.

При этом используются значения функции не только в концах интервала, но и в точках, лежащих внутри интервала.

31. Методы Рунге – Кутта. Формулы Эйлера и Адамса.

Пусть требуется численно решить задачу Коши для дифференциального уравнения 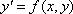(1)

при заданном начальном условии 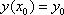(2)

Зададим некоторый достаточно малый шаг сетки вычислений h. Тогда для каждого 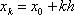значение искомой функции (решения задачи (1)-(2)) можно последовательно вычислить по формуле Эйлера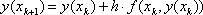

Формула Эйлера является достаточно простой для программирования, однако, ее погрешность достаточно велика и сильно зависит от величины h.

Более точной является неявная формула Адамса: ,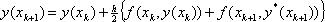

где значение 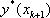вычисляется по формуле Эйлера.

При использовании описанных формул следует учитывать, что погрешность увеличивается с каждым шагом вычислений.
32.Конечно-разностные методы решения задачи Коши.

Конечно-разностные методы – методы, в которых значения функции в конце каждого интервала зависят, в общем случае, от значений функции в конце предшествующих интервалов.

Разностные уравнения:

1)

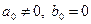
В этом случае, уравнения называются явным или экстраполяционным.

К этому виду относится формула Эйлера.

В этом случае каждое значение выражается через значение предшествующей функции.

При , в правой части отсутствует.

2)

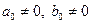
Это уравнение называется неявным или интерполяционным.

В этом случае искомое значение входит в уравнение нелинейным образом, или для его нахождения, в общем случае, требуется применение итерационных методов.

К этому классу относится формула Адамса, основанная на трапеции.

Существует также множество других методов, к которым относятся методы неопределенных коэффициентов и т.д.

Методы решения дифференциальных уравнений первого порядка практически без изменения переносятся на случай систем линейных дифференциальных уравнений первого порядка:

Отличие заключается в том, что вместо производных по скалярным переменным появляются производные по векторным переменным.

Метод Эйлера для этой системы записывается в виде:

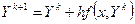
Верхний индекс обозначает номер итерации.

Это будет система уравнений первого порядка.

Дата добавления: 2015-04-24