Вопрос 22

Вопрос

Матрица. Виды матриц. Операции над матрицами: сложение, умножение на число, перемножение, транспонирование. Формулы для элементов матриц-результатов. Свойства этих операций

Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов, которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы.

Вид Матриц: 1) Квадратная. 2) Диагональная. 3)Нулевая. 4) Единичная.

Действие на матрицами: 1) Сложение. 2)Вычитание. 3)Умножение. 4)Транспонирование. 5)Сопряжение.

Свойства операций: 1.1) Коммутативность. 1.2) Ассоциативность. 2.1) Коммутативность. 2.2) Ассоциативность. 3.1) Распределение. 3.2) A*(B*C)=(A*B)*C

1. A+B=B+A;

2. (A+B)+C=A+(B+C);

3. ;

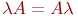4. ;

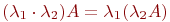5. ;

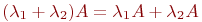6. ;

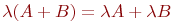7. A+0=A;

8. A+(-A)=0.

Определитель матрицы является многочленом от элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равно).

2 Вопрос

1. Определители матриц. Рекуррентное определение. Вычисление определителей порядков 2 и 3 (док-во). Минор и алгебраическое дополнение элемента. Понижение порядка определителя.

В матрице порядка n алгебраическим дополнением элемента, стоящего на пересечении k -го столбца и l -й строки, называется определитель порядка (n - 1), получаемый из данной матрицы вычеркиванием в нем строки и столбца, на пересечении которых стоит этот элемент, причем к этому определителю присоединяется множитель (-1) ^{k + l} , где (k + l) - сумма номеров вычеркнутой строки и столбца. Алгебраическое дополнение элемента, рассматриваемое без множителя (-1) ^{k + l} , называется минором этого элемента.

Определитель равен сумме произведений каждого элемента некоторой строки (или столбца) на его алгебраическое дополнение.

Рекуррентное определение: Определителем квадратной матрицы 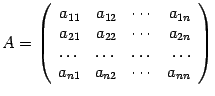порядка 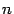, , 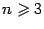называется число 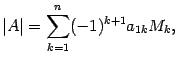где 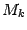-- определитель матрицы порядка 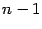, полученной из матрицы 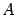вычеркиванием первой строки и столбца с номером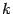

3 Вопрос Способ упрощения определителя на основании свойств Метод понижения порядка определителя основан на последовательном приведении всех столбцов к нулю кроме верхнего члена столбца. (приводить к нулю методом Гаусса

4 вопрос Обратная матрица. Определение. Теоремы о единственности, определителе, существовании и вычислении обратной матрицы (с доказательствами). Присоединённая матрица

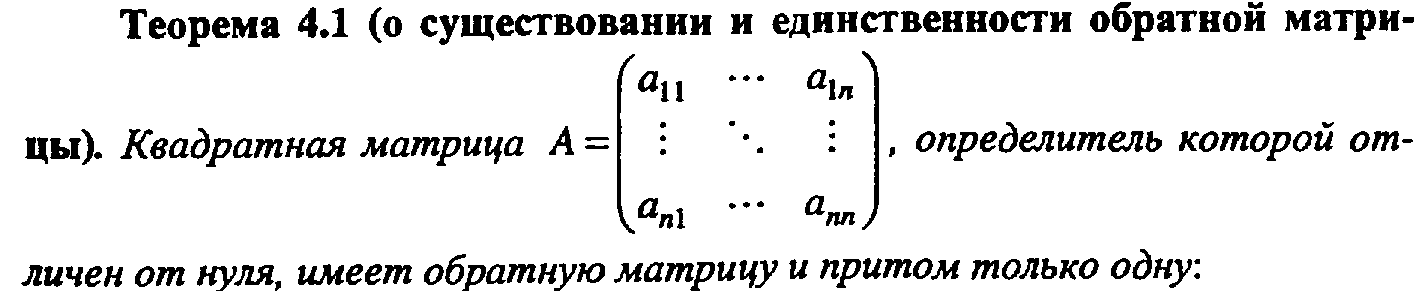
Присоединённая матрица – Транспонированная матрица алгебраических дополнений

Вопрос 5 Свойства обратной матрицы:

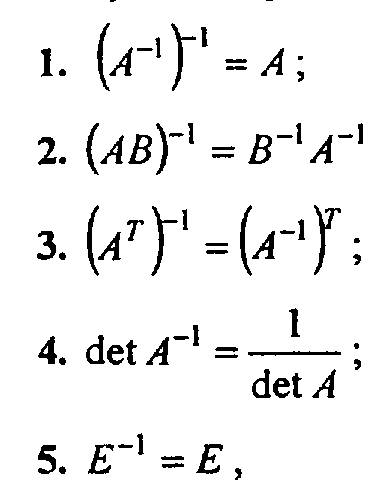
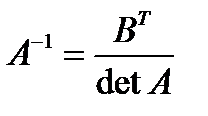, где В- матрица алгебраических дополнений. Находится через миноры элементов исходной матрицы умноженные на 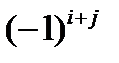, где i и j строка и столбец элемента.

Решение простейших линейных матричных уравнений A*X=С=>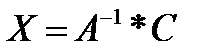

Вопрос 6 Системы линейных алгебраических уравнений. Основные понятия. Матричная форма записи. Правило Крамера (доказательство). Условия его применения

Условие применения правила Крамера- неравенство нулю общего определителя.

Вопрос 7. ЛЗ и ЛНЗ строки и столбцы.

ЛЗ(линейно-зависимые) – можно составить линейную комбинацию строк\столбцов.

ЛНЗ(линейно-независимые) – нельзя составить линейную комбинацию строк\столбцов.

Общее условие равенства нулю определителя.- Если одна строка матрицы является линейной комбинацией остальных строк, то определитель такой матрицы равен нулю.

Вопрос 8. Миноры матрицы, определение, свойство. Базисный минор матрицы (определение). Теорема о базисном миноре. Ранг матрицы (определение). Теорема о ранге матрицы.

Минор матрицы – определитель матрицы N-1xN-1. На тех строках\столбцах, которые вычеркнули называются основные миноры. А те которые не на вычеркнутых строках\столбцах – называются дополнительными минорами. Базисный минор – минор высшего порядка не равный 0.

Теорема о базисном миноре: Строки\столбцы ЛНЗ. Остальные строки\столбцы можно выразить через столбцы\строки базисного минора.

Теорема о ранге:Ранг матрицы равен порядку базисного минора. И равен максимальному числу ЛНЗ строк\столбцов.

Вопрос 9. Вычисление ранга матрицы методом элементарных преобразований. Нахождение одного из базисных миноров. Условие совместности системы (теорема Кронекера-Капелли)

Ранг можно посчитать через Гаусса. Вычеркиваем кол-во строк\столбцов равных рангу и находим не равный 0 минор!.

Теорема Кронекера-Капелли:Если ранг обычной, равен рангу расширенной матрицы, то система совместна!.

Вопрос 10. Общий метод решения совместной системы из m линейных алгебраических уравнений с n неизвестными. Условия единственности и множественности решений системы.

Единственное решение, когда кол-во переменных равно кол-ву уравнений. И детерминант общей матрицы не равен нулю. Вид преобразованной матрицы- треугольный

Множество решений когда вид преобразованной матрицы- трапецевидный

Признак несовместности системы: наличие строки вида 00000| а

Вопрос 11. Метод Гаусса последовательного исключения неизвестных. Его матричная форма. Прямой и обратный ходы метода Гаусса. Выбор базисных переменных. Получение общего решения.

Из любой строки\столбца можно вычесть\прибавить\умножить\разделить на другую строку\столбец. А так же сократить\умножить на число любую строку\столбец. Можно вычеркнуть одинаковые. Базисные переменные можем сами выбрать, как и свободные. Выражаем базисные, через свободные находим общее решение, и ФСР.

Вопрос 12. Однородная система линейных уравнений, её свойства. Теорема о существовании линейно независимых решений. Фундаментальная система решений. Структура общего решения.

Однородной системой называется система уравнений, где каждое уравнение равно 0! Есть точно тривиальное решение(нулевое решение). Если определитель равен 0, то есть хоть одно не тривиальное решение. Фундаментальная система решений – Если у нас есть 2 и более свободных переменных, то поочередно меняем значение переменных 1 и 0 и получаем ФСР. Общее решение – выражение базисных переменных, через свободные.

Вопрос 13. Связь решений соответствующих неоднородной и однородной систем линейных алгебраических уравнений. Структура общего решения неоднородной системы

Разность решений не однородной системы, дает решение однородной системы. И крутим вертим шаверму.

Вопрос 14. Собственные векторы и собственные значения матрицы. Определение. Арифметический вектор. Характеристическое уравнение матрицы (док-во). Нахождение собственных векторов как ФСР

Собственный вектор аналог ФСР. находим его через собственные значения матрицы.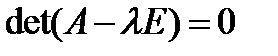

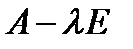решение данной системы уравнений дает вектор соответствующий данной лямде. Для каждой лямбды ищем свой собственный вектор..

Собственный вектор – умножение его на халфу = значению А*Х. Собственный вектор удовлетворяет условию:

X на лямбду= АХ

Вопрос 15. Геометрический вектор: определение, модуль. Равенство, коллинеарность и компланарность векторов. Линейные операции над векторами: определение, свойства.

Направленный отрезок на плоскости. Модуль: 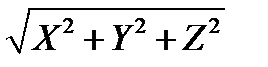. Коллинеарность когда 2 вектора параллельны. Компланарность 3 и более вектора через которые можно провести плоскость.

Линейные операции сумма, умножение на число (и обратные) Свойства а+в= в+а; a(b+c)=ab+ac;

a+0=a;a(bc)=(ab)c.

Вопрос 16. Системы координат на плоскости и в пространстве (аффинная, декартова). Базисы. Координаты вектора (определение). Линейные операции над векторами в координатной форме.

Декартова система координат - это такая система, где векторы направленности равны по 1. Базис – любые 3 вектора исходящие из одной точки. Координаты вектора линейная комбинация базисных векторов и коэффициенты при ни и есть координаты. Операции: сложение, умножение на число и обратные им действия.При сложении складываем соответствующие координатя, при умножении- умножаем на число.

Вопрос 17. Координаты точки (определение). Выражение координат вектора через координаты его начала и конца (доказательство). Деление отрезка в заданном отношении (доказательство).

Координаты точки это координаты радиус вектора построенного на этой точке и начале координат

Формула координат вектора: из конца вычитаем начало вектора. Координаты точки делящей отрезок на части относящиеся как халфа 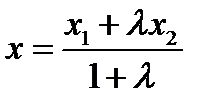тоже самое для y,z.

Вопрос 18. Скалярное произведение векторов. Определение, свойства, выражение через декартовы координаты сомножителей (док-во), применение. Направляющие косинусы вектора.

Скалярное произведение – представляем как умножение матриц составленных через координаты векторов.. Свойства: a*b=b*a; k*(a*b) = (k*a)*b…

Вопрос 19. Векторное произведение векторов. Определение, геометрический смысл, выражение через декартовы координаты сомножителей (док-во), свойства, применение.

Векторное произведение векторов – вектор с координатами равными коэффициентам при i,j,k при подсчете определителя матрицы этих векторов. Свойсвта: модуль векторного произведения- площадь параллелограмма образованного через них. Или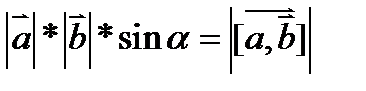

Вопрос 20. Смешанное произведение векторов. Определение, геометрический смысл, выражение через декартовы координаты сомножителей (док-во), применение, свойства.

Смешанное произведение векторов – ([a,b],c) или определитель матрицы из этих векторов. Свойство: Объем параллепипеда построенного на этих векторах.

Вопрос 21. Прямая линия на плоскости. Уравнения: с угловым коэффициентом, общее, параметрические, каноническое. Расстояние от точки (док-во). Угол между прямыми, точка их пересечения

Уравнение прямой: Ах+Ву+С = 0. Расстояние от точки до прямой вычисляется по формуле: 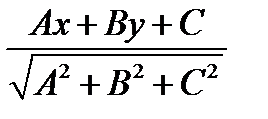. Угол между прямыми: делаем из прямых векторы направляющие и формулой: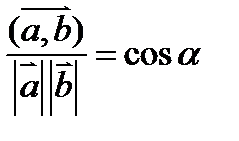

Вопрос 22. Плоскость в пространстве. Уравнения: общее, компланарное. Расстояние от точки (док-во). Угол между плоскостями. Взаимное расположение двух плоскостей.

Уравнение плоскости аналогично прямой, но + еще Z координата. Расстояние так же. Угол так же, но вместо направляющего вектора берем нормаль к плоскости.

Если координаты при переменных в уравнениях пропорциональны то плоскости параллельны., если нет- то пересекаются. Еще можно по нормалям если они параллельны, то плоскости параллельны.

Вопрос 23,24. Две прямые в пространстве. Анализ трёх типов их взаимного расположения. Расстояния: между точкой и прямой, между параллельными прямыми, между непараллельными прямыми (док-во).

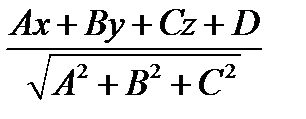от точки до прямой\плоскости(на плоскости\ пространстве).

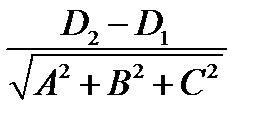
расстояние между прямыми\плоскостями

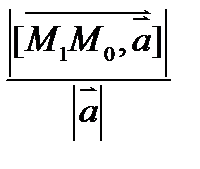    от точки до прямой до прямой в проствранстве. а – направляющий вектор к прямой.

Если координаты векторов пропорциональны, то они параллельны. Если не пропорциальны, решаем систему уравнений. Прямые в пространстве параллельны если параллельны их направляющие. Лежат в одной плосткости если смешанное произведение напрвляющих и вектора из точек принадлежащих этим прямым- =0. А если смешанное произведение не равно нулю то не лежат в одной плоскости.

Вопрос 25.

Кривые 2-го порядка на плоскости. Их типы, определения как геометрических мест точек (относительно фокусов), иррациональные и канонические уравнения (док-во). Построение кривых.

Типы:

1) Парабола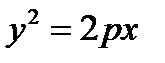

P\2 - фокус параболы –Р\2 точка прохождения директрисы. R – фокальный радиус. О – вершина параболы. Геом. Место точек: равноудаленность от фокуса и директрисы.

2) Гипербола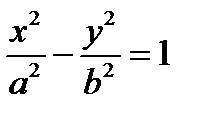

a,b > 0, полуоси гиперболы. 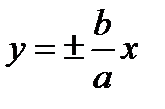асимптоты. 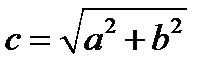- фокус гиперболы

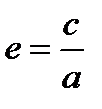степень сплюснутости(энкцентриситет). Геометрическое место точек, для которых отношение расстояния до фокуса и до заданной прямой, называемой директрисой, постоянно и больше единицы, называется гиперболой. Заданная постоянная ε > 1 называется эксцентриситетом гиперболы.

3) Эллипс 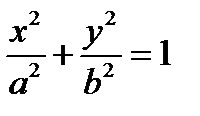a,b полуоси. 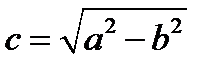фокус. Экцентриситет такой же как и у гиперболы. Эллипсом называется геометрическое место точек плоскости, сумма расстояний которых от двух данных точек этой же плоскости, называемых фокусами эллипса, постоянна.

Вопрос 26. Общее уравнение кривой 2-го порядка на плоскости. Его преобразование к каноническому виду. Канонические уравнения смещённых и повёрнутых кривых.

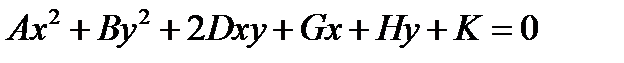Преобразовать к каноническому виду: Если кривая 2ого порядка невырожденная, то для нее найдется такая система координат, в которой уравнение кривой имеет 1 из 3ех канонических видов (эллипс, гипербола, парабола

).

Вопрос 27,28. Поверхности 2-го порядка: эллипсоид, конус и гиперболоиды. Канонические уравнения, их отличительные особенности. Исследование формы методом сечений. Эскизы.

2. Поверхности 2-го порядка: параболоиды и цилиндры. Канонические уравнения, их отличительные особенности. Исследование формы методом сечений. Эскизы.

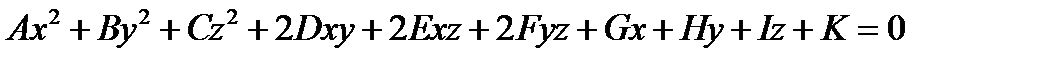
1) Эллипсоид 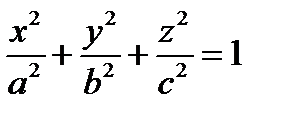вытянутый шар

2) Гиперболоид

2.1) Однополостный 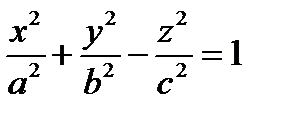две чашки соединенные днами

2.2) Двухполостный 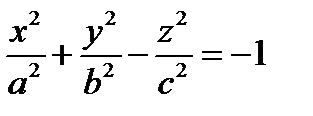две чашки разъединенные

3) Конус 2ого порядка 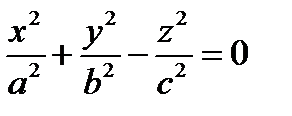два конуса соединенные вершинами

4) Параболоид

4.1) эллиптический 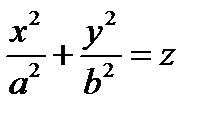ветчина

4.2) гиперболический 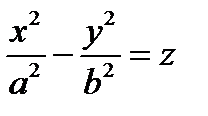седло

5) Цилиндр

5.1) Эллиптический 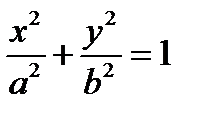сплюснутый стакан

5.2) Параболический 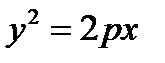половина стенки стакана

5.3 гиперболический 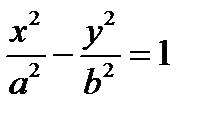две разрезанные стенки, вывернутые.

Вопрос 29 Знаменатель дробей характеризует сплюстнутость\вытянутость по соотв осям. Числа отнимаемые от переменных означает смещение фигуры от начала координат.

Полупроводниковые диоды, классификация. Выпрямительные низкочастотные диоды, особенности германиевых и кремниевых диодов. Температурные диапазоны работы.

Классификация полупроводниковых диодов

По исходному полупроводниковому материалу диоды делятся на две основные группы: германиевые и кремниевые. Первые работают при температурах не выше +70°С, а вторые – до +125-150°С.

По конструктивно-технологическому признаку также различают две разновидности диодов: точечные и плоскостные. У точечных диодов (рис. а) выпрямляющий контакт образуется в точке касания полупроводниковой пластинки острием металлической иглы, причем пропускное направление соответствует прохождению тока от иглы к пластинке. У плоскостных диодов (рис. б, в) выпрямляющими свойствами обладает поверхность раздела двух областей полупроводника с разными типами проводимости (дырочной p и электронной n) внутри монокристаллического объема полупроводника (p-n переход). Наиболее распространенными плоскостными диодами являются так называемые сплавные, у которых p-n переход образуется в результате рекристаллизации сплава исходного полупроводника с помещенной на его поверхности таблеткой примесного вещества (рис. б).

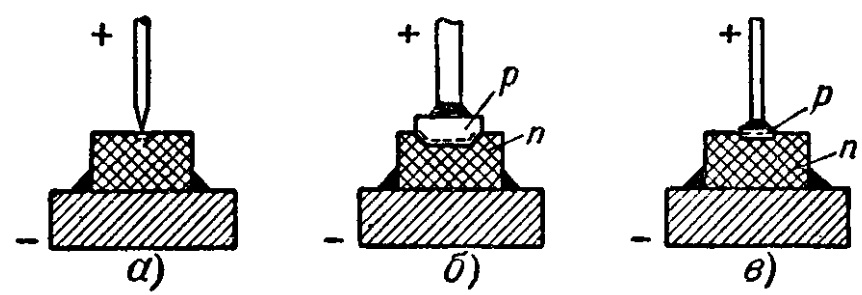
Устройство полупроводниковых диодов различных типов: а) - точечного; б) - плоскостного сплавного; в) - микросплавного

Сплавные диоды позволяют пропускать значительно большие токи и отличаются лучшим постоянством характеристик, но обладают повышенными емкостями, что ограничивает их применение на высоких частотах. Промежуточными свойствами обладают микросплавные диоды (рис. в). Они изготавливаются путем электролитического осаждения тонкой пленки примесного вещества на поверхность монокристаллической пластинки исходного полупроводника и последующего вплавления этой примеси.

По областям применения различают диоды универсального назначения, силовые выпрямительные диоды, стабилизаторы напряжения («опорные» диоды) и ряд разновидностей диодов специализированного назначения (смесительные и модуляторные диоды, диоды для умножения частоты, для параметрических усилителей и др.). Выпускаются также высоковольтные выпрямительные столбы, состоящие из нескольких однотипных диодов, включенных последовательно.

Рис. 1.10 Условные графические обозначения: а – выпрямительные и универсальные;
б – стабилитроны; в – двухсторонний стабилитрон; г – туннельный диод;
д – обращенные диоды; е – варикап; ж – фотодиодов; з – светодиод

Дата добавления: 2015-04-24