
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Аналитическая геометрия
|
|
|
|
1.
Прямая на плоскости: общее уравнение; уравнение в отрезках; уравнение с угловым коэффициентом; уравнение прямой, проходящей через две данные точки. Нормаль прямой. Вычисление угла между прямыми. Условия параллельности и перпендикулярности прямых.
1)Общее уравнение прямой.
Теорема об общем уравнении прямой.
В ДПСК любая прямая определяется уравнением  степени и наоборот любое уравнение степени и наоборот любое уравнение  степени определяет прямую. степени определяет прямую.
|
Доказательство

|
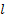 – прямая на плоскости
– прямая на плоскости

|
 (фиксированная точка прямой)
(фиксированная точка прямой)
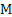 (
(  ) (произвольная точка прямой)
) (произвольная точка прямой)
| M |
 (произвольный вектор прямой
(произвольный вектор прямой  )
)
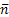 - вектор нормали
- вектор нормали

|


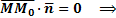
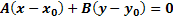 (1)
(1)
уравнению (1) удовлетворяют все точки прямой  .
.
(1) – уравнение прямой  с нормальным вектором
с нормальным вектором  проходящей через
проходящей через 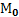 .
.
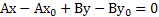


 (2)
(2)
Уравнение (2) – общее уравнение прямой 
Анализ общего уравнения прямой:
1) Если С=0  прямая проходит через (0;0)
прямая проходит через (0;0)
2)
| y |
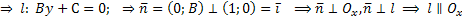
3) Если В=0 
4)
| M |
| y |
 - прямая совпадает с
- прямая совпадает с 
5) Если B=0, С=0  - прямая совпадает с
- прямая совпадает с 

|

|

|
| A |

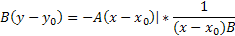
| x |
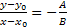

|
| x |
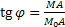
 – угол наклона прямой к
– угол наклона прямой к 
 - угловой коэффициент прямой
- угловой коэффициент прямой  (3)
(3)
(3) – уравнение прямой, проходящей через точку (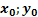 ) угловым коэффициентом k.
) угловым коэффициентом k.

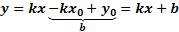 (4)
(4)
(4) – уравнение прямой с угловым коэффициентом
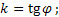
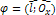 ; b – отрезок, отсекаемый прямой от оси
; b – отрезок, отсекаемый прямой от оси 
Анализ уравнения прямой с угловым коэффициентом:
1) Если k=0 
2) Если b=0 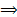
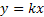 – прямая проходит через (0;0)
– прямая проходит через (0;0)
3)Уравнение прямой, проходящей через 2 точки.
Пусть  - 2 фиксированные точки;
- 2 фиксированные точки;  – произвольная точка.
– произвольная точка.
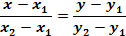
|
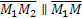
| (5) |
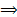
|

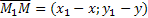
(5) – уравнение прямой, проходящей через 2 точки

 ,
,  любой вектор параллельный прямой называется направляющим вектором.
любой вектор параллельный прямой называется направляющим вектором.  – направляющий вектор.
– направляющий вектор.
|
|
|
| (6) |

(6) – каноническое уравнение прямой, где 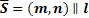 .
.
4)Уравнение прямой «в отрезках»
Пусть  не проходит через начало координат
не проходит через начало координат
Пусть 
Подставим  в (5)
в (5) 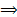

(7) – уравнение прямой «в отрезках»
a,b – отрезки отсекаемые прямой от осей  соответственно.
соответственно.


| 

| |
| Условие параллельности | 

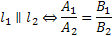
| 
|
| Условие перпендикулярности | 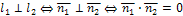
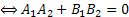
| 
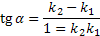
|
| Угол между прямыми | 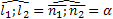
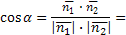

| 
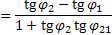
|
2.
Плоскость в пространстве: общее уравнение; уравнение в отрезках; уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору; уравнение плоскости, проходящей через три данные точки. Нормаль плоскости. Вычисление угла между плоскостями. Условия параллельности и перпендикулярности плоскостей.
1)Общее уравнение плоскости.
Теорема об общем уравнении плоскости.
Каждая плоскость задается уравнением  степени в ДПСК и наоборот каждое уравнение степени в ДПСК и наоборот каждое уравнение  степени определяет плоскость. степени определяет плоскость.
|
В ДПСК любая прямая определяется уравнением  степени и наоборот любое уравнение
степени и наоборот любое уравнение  степени определяет прямую.
степени определяет прямую.
Доказательство
Пусть P-плоскость
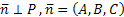
 -фиксированная точка плоскости Р
-фиксированная точка плоскости Р
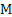 (
( ) – произвольная точка плоскости P
) – произвольная точка плоскости P
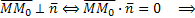
 (1)
(1)
уравнению (1) удовлетворяют все точки плоскости P с  проходящей через точку
проходящей через точку 
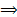 (1) –уравнение плоскости.
(1) –уравнение плоскости.


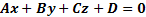 (2)
(2)
(2) – общее уравнение плоскости
Анализ общего уравнения прямой:
1) Если D=0  плоскость проходит через (0;0;0)
плоскость проходит через (0;0;0)
2) Если А=0 
3) Если В=0 
4) Если C=0 
5) Если А=0, D=0 

6) Если B=0, D=0 

7) Если C=0, D=0 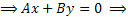

8) Если А=0, B=0 
9) Если B=0, C=0 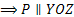
10) Если А=0, C=0 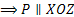
11) Если А=0, B=0 C=0  ; уравнение XOY:Z=0
; уравнение XOY:Z=0
12) Если B=0, C=0 D=0  ; уравнение YOZ:X=0
; уравнение YOZ:X=0
13) Если А=0, C=0 D=0 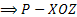 ; уравнение XOZ:Y=0
; уравнение XOZ:Y=0
Если A,B,C,D 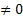 , то плоскость называется плоскостью общего положения.
, то плоскость называется плоскостью общего положения.
2)Уравнение плоскости «в отрезках».
 Пусть
Пусть 



(3) – уравнение плоскости «в отрезках»
Y=0, z=0  - точка пересечения
- точка пересечения 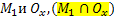
|
|
|
X=0, z=0 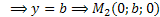 - точка пересечения
- точка пересечения 
X=0, y=0 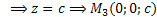 - точка пересечения
- точка пересечения 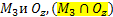
a,b,c - отрезки отсекаемые Р от осей координат
Плоскость, не проводящую через начало координат удобно строить по уравнению «в отрезках»
3)Уравнение плоскости проходящей через 3 точки.
Пусть  - три фиксированные точки плоскости, не лежащие на одной прямой, а точка M(x;y;z) –произвольная точка плоскости.
- три фиксированные точки плоскости, не лежащие на одной прямой, а точка M(x;y;z) –произвольная точка плоскости.
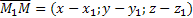

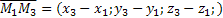
 - компланарны
- компланарны 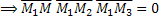
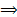

(4) – уравнение плоскости, проходящей через 3 заданные точки.
Вычисление угла между плоскостями.
Угол между плоскостями – любой из двугранных углов, образованных плоскостями.

 ;
; 
Условие параллельности плоскостей.
ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 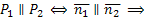

Условие перпендикулярности плоскостей.
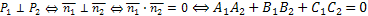
3.
Прямая в пространстве: общие, параметрические и канонические уравнения, их эквивалентность; уравнения прямой, проходящей через две данные точки. Вычисление угла между прямыми. Условия параллельности и перпендикулярности прямых.
Уравнение прямой в пространстве задается пересечением двух плоскостей.
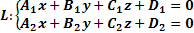 (1) – общее уравнение прямой в пространстве.
(1) – общее уравнение прямой в пространстве.
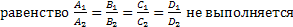
Пусть


| (2)-канонические уравнения прямой в пространстве |


(3) – параметрические уравнения.
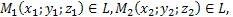
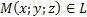 - произвольная точка прямой.
- произвольная точка прямой.
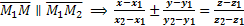 (4)
(4)
(4) – уравнение прямой, проходящей через 2 заданные точки.
Углом между двумя прямыми в пространстве называется любой из углов, образованный двумя прямыми проходящими через данную точку параллельно этим прямым 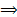 Угол между прямыми – угол между векторами параллельными этим прямым.
Угол между прямыми – угол между векторами параллельными этим прямым.

Условие параллельности прямых.
 (условие компланарности)
(условие компланарности)
Условие перпендикулярности прямых.

4.
Плоскость и прямая в пространстве. Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости. Пересечение прямой и плоскости.
Углом между прямой и плоскостью называется любой из двух смежных углов между прямой и её проекцией на эту плоскость.

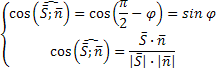
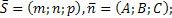
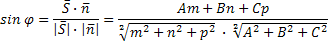
Условие перпендикулярности прямой и плоскости.

Условие параллельности прямой и плоскости.
 =0;
=0;
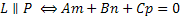
Пересечение прямой и плоскости.

Для нахождения точки пересечения прямой и плоскости подставим правые части формул (1) в общее уравнение плоскости.
|
|
|
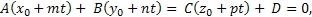
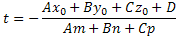
1) Если  , то находим значение t, подставляем в уравнение прямой (1) и находим точку пересечения M(x,y,z).
, то находим значение t, подставляем в уравнение прямой (1) и находим точку пересечения M(x,y,z).
2) Если 
при этом если: а) 
б)  (L и P не пересекаются)
(L и P не пересекаются)
5.
Эллипс. Его основное геометрическое свойство, фокусы, эксцентриситет.
Кривой 2 порядка называется линия, имеющая в ДПСК  уравнение второй степени относительно x и y;
уравнение второй степени относительно x и y; 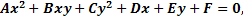 (1)
(1)
где  .
.
(1) - общее уравнение кривой второго порядка. К кривым второго порядка относятся: парабола, гипербола, окружность, эллипс.
Эллипс – кривая имеющая в некоторой ДПСК уравнение  (2), где a и b - полуоси,
(2), где a и b - полуоси,  .
.
(2) –каноническое уравнение эллипса.
Если  , то -большая,
, то -большая,  -малая, если
-малая, если  , то наоборот.
, то наоборот.
Точки 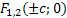 при
при  и
и  - фокусы эллипса.
- фокусы эллипса.
Свойства эллипса:
1. Для любых точек эллипса сумма расстояний до двух фиксированных точек (фокусов) есть величина постоянная и равная  если
если  и
и 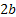 если
если  .
.
2. Отношение расстояния между фокусами к большой оси – эксцентриситет эллипса  .
.
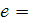
 <1 (если
<1 (если  )
)  < 1 (если
< 1 (если  )
)
3. Параметрические уравнения эллипса: 
Замечание:  эллипс с центром в точке
эллипс с центром в точке 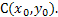
6.
Гипербола. Её основное геометрическое свойство, фокусы, эксцентриситет.
Кривой 2 порядка называется линия, имеющая в ДПСК  уравнение второй степени относительно x и y;
уравнение второй степени относительно x и y; 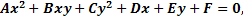 (1)
(1)
где  .
.
(1) - общее уравнение кривой второго порядка. К кривым второго порядка относятся: парабола, гипербола, окружность, эллипс.
Гипербола – кривая 2-го порядка, имеющая в некоторой ДПСК уравнение 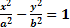 , (2)
, (2)
где a-действительная и b-мнимая полуоси или  , (3) где а-мнимая и b-действительная полуоси.
, (3) где а-мнимая и b-действительная полуоси.
- Фокусы гиперболы 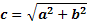
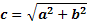
|

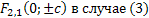
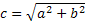
Свойства гиперболы:
1. Для любых точек гиперболы модуль разности их растояний до двух фиксированных точек(фокусов) есть величина постоянная и равная  если
если  -действительная и
-действительная и 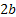 если
если  -действительная полуось.
-действительная полуось.
2. 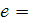
 (а-действ.)
(а-действ.)  (b-действ.)
(b-действ.)
3.  обладают свойством, что точки гиперболы при
обладают свойством, что точки гиперболы при 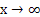 подходят сколь угодно близко к этим прямым. Эти прямые называтются асимтотами гиперболы.
подходят сколь угодно близко к этим прямым. Эти прямые называтются асимтотами гиперболы.
Замечание:
1) Уравнение  также определяет гиперболу (равнобочную).
также определяет гиперболу (равнобочную).
2) Ур-е 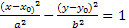 гипербола со смещенным в точку C(x0,y0) центром. (Где a-действительная и b-мнимая полуоси)
гипербола со смещенным в точку C(x0,y0) центром. (Где a-действительная и b-мнимая полуоси)
|
|
|
 гипербола со смещенным в точку C(x0,y0) центром.(где а-мнимая и b-действительная полуоси.)
гипербола со смещенным в точку C(x0,y0) центром.(где а-мнимая и b-действительная полуоси.)
7.
Парабола. Е основное геометрическое свойство, фокус, директриса.
Кривой 2 порядка называется линия, имеющая в ДПСК  уравнение второй степени относительно x и y;
уравнение второй степени относительно x и y; 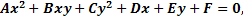 (1)
(1)
где  .
.
(1) - общее уравнение кривой второго порядка. К кривым второго порядка относятся: парабола, гипербола, окружность, эллипс.
Парабола – кривая 2-ого порядка, имеющая в некоторой ДПСК уравнение 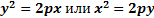 .(канонические уравнения)
.(канонические уравнения) 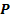 -параметр параболы.
-параметр параболы.  (ветви влево);
(ветви влево);  -расстояние между
-расстояние между  и
и  .
.
Основное свойство параболы:
Все точки параболы равноудалены от фиксированной точки (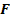 ) и от фиксированной прямой (
) и от фиксированной прямой ( )
)
Замечание:
Уравнение параболы с вершиной в точке 
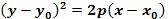
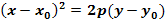
8.
Параллельные перенос системы координат. Приведение общего уравнения кривой второго порядка к каноническому виду.
| z |
| z’ |
| M |
 ДПСК
ДПСК  .
.
В системе 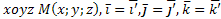 .
.
В системе 
| O’ |
| y’ |
 (1)
(1)
| x |
| O |
| y |
| x’ |
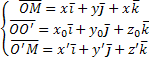 (2)
(2)
Из (1) и (2) 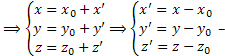 Формулы перехода от системы
Формулы перехода от системы  , т.е. формулы параллельного переноса системы координат.
, т.е. формулы параллельного переноса системы координат.
Приведение общего уравнения кривой второго порядка к каноническому виду:
Случай 
Дано общее уравнение кривой 2-го порядка: 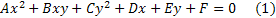
В этом случае уравнение приводится к каноническому виду с помощью выделения полных квадратов по переменным  . При этом используется формула полного квадрата s w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/></w:rPr><m:t>)</m:t></m:r></m:e><m:sup><m:r><m:rPr><m:sty m:val="bi"/></m:rPr><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/></w:rPr><m:t>2</m:t></m:r></m:sup></m:sSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
. При этом используется формула полного квадрата s w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/></w:rPr><m:t>)</m:t></m:r></m:e><m:sup><m:r><m:rPr><m:sty m:val="bi"/></m:rPr><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/></w:rPr><m:t>2</m:t></m:r></m:sup></m:sSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  После выделения полных квадратов уравнение (1) принимает вид:
После выделения полных квадратов уравнение (1) принимает вид:  (2)
(2) 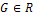 , можно сказать что если:
, можно сказать что если:
1. Коэффициенты A и B одного знака то:
a) При  такого же знака, то уравнение (2) задает эллипс(при А=В – окружность)
такого же знака, то уравнение (2) задает эллипс(при А=В – окружность)
b) При 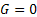 уравнение (2) задает одну точку с координатами
уравнение (2) задает одну точку с координатами 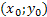 – вырожденный эллипс
– вырожденный эллипс
c)  уравнению (2) не удовлетворяет ни одна точка – мнимый эллипс.
уравнению (2) не удовлетворяет ни одна точка – мнимый эллипс.
2.  то:
то:
a) При  уравнение (2) задает гиперболу.
уравнение (2) задает гиперболу.
b) При 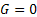
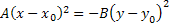 предположим что
предположим что 
 – пара прямых пересекающихся в точке
– пара прямых пересекающихся в точке 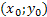
3.  уравнение (2) задает параболу (или пару параллельных прямых)
уравнение (2) задает параболу (или пару параллельных прямых)
Случай 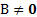
Алгоритм приведения (1) к каноническиму виду.
1) Составляем 
2) Одим собстевенные числа 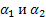 и соответствующие или собственные векторы
и соответствующие или собственные векторы  ,
, 
3) Нормируем векторы  т.е. находим их орт-векторы
т.е. находим их орт-векторы 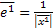 ,
, 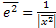 Пусть
Пусть  ,
, 
4) 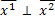 , то и
, то и  образуют базис на плоскости. Пусть S – матрица перехода от базиса
образуют базис на плоскости. Пусть S – матрица перехода от базиса  к
к 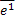 ,
,  .
. 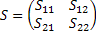 тогда
тогда  (2)
(2)
5) Подставляем (2) в (1). После преобразования уравнение (1) примет вид:
 , где
, где  .
.
| y |
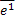 , OY’ – направлена вдоль вектора
, OY’ – направлена вдоль вектора 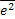 , O – общее начало.
, O – общее начало.
| x’ |
| y’ |

|
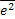
|
| x |
| O |
6) Дальнейшее приведение этого уравнеиня к каноническому виду осуществляется как в случае 1.
9.
Полярная система координат. Ее связь с ДПСК.
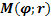
|
| r |
 3)единицей масштаба.
3)единицей масштаба.
Произвольная точка плоскости М имеет в ПСК 2 координаты.

|
 - полярный угол
- полярный угол  и r – полярный радиус,
и r – полярный радиус, 
| y |
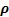
|
Совместить в начале и направить полярную ось по  .
.
Переход от ПСК в ДПСК.
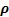
|
| r |

|
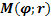
|
| x |
| x |
| y |
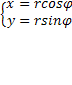
Переход от ПСК в ДПСК.


|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 519; Нарушение авторских прав?; Мы поможем в написании вашей работы!