Формула полной вероятности

Предположим, что событие 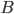может осуществляться только с одним из несовместных событий 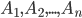. Например, в магазин поступает одна и та же продукция от трех предприятий в разном количестве. Существует разная вероятность выпуска некачественной продукции на разных предприятиях. Случайным образом отбирается одно из изделий. Требуется определить вероятность того, что это изделие некачественное (событие 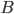). Здесь события — это выбор изделия из продукции соответствующего предприятия.

В этом случае вероятность события 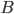можно рассматривать как сумму произведений событий

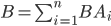
По теореме сложения вероятностей несовместных событий получаем

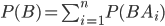
Используя теорему умножения вероятностей, находим

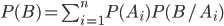(3.1)

Формула (3.1) носит название формулы полной вероятности.

Пример. Для рассмотренного выше случая с поступлением товара в магазин от трех предприятий зададим численные значения. Пусть от первого предприятия поступило 20 изделий, от второго — 10 изделий и от третьего — 70 изделий. Вероятности некачественного изготовления изделия на предприятиях соответственно равны 0,02; 0,03 и 0,05.

Определить вероятность взятия некачественного изделия.

Решение. Вероятности событий 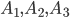будут равны P(А₁) = 0,2; P(А₂) = 0,1; P(А₃) = 0,7. Используя формулу (3.1), находим

P(B) = 0,2×0,02 + 0,1×0,03 + 0,7×0,05 = 0,042.

10.Формула Бейеса.

Пусть событие 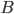происходит одновременно с одним из 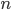несовместных событий 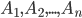. Требуется найти вероятность события 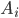, если известно, что событие 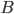произошло.

На основании теоремы о вероятности произведения двух событий можно написать

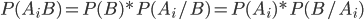
Откуда

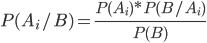
или

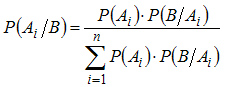(3.2)

Формула (3.2) носит название формулы Байеса.

11.Основные формулы комбинаторики.
Комбинаторика изучает количества комбинаций, подчиненных определенным условиям, которые можно составить из элементов, безразлично какой природы, заданного конечного множества. При непосредственном вычислении вероятностей часто используют формулы комбинаторики. Приведем наиболее употребительные из них.

Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок

P_n = n!,

где n! = 1 * 2 * 3... n.

Заметим, что удобно рассматривать 0!, полагая, по определению, 0! = 1.

Размещениями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком. Число всех возможных размещений

A^m_n = n (n - 1)(n - 2)... (n - m + 1).

Сочетаниями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются хотя бы одним элементом. Число сочетаний

С ^m_n = n! / (m! (n - m)!).

примеры перестановок, размещений, сочетаний

Подчеркнем, что числа размещений, перестановок и сочетаний связаны равенством

A^m_n = P_mC ^m_n.

З а м е ч а н и е. Выше предполагалось, что все n элементов различны. Если же некоторые элементы повторяются, то в этом случае комбинации с повторениями вычисляют по другим формулам. Например, если среди n элементов есть n₁ элементов одного вида, n₂ элементов другого вида и т.д., то число перестановок с повторениями

P_n (n₁, n₂,...) = n! / (n₁! n₂!...),

где n₁ + n₂ +... = n.

При решении задач комбинаторики используют следующие правила:

П р а в и л о с у м м ы. Если некоторый объект А может быть выбран из совокупности объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно m + n способами.

П р а в и л о п р о и з в е д е н и я. Если объект А можно выбрать из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А, В) в указанном порядке может быть выбрана mn способами.

12.Формула Бернулли.

Предположим, что несколько одинаковых машин в одних и тех же условиях перевозят груз. Любая машина может выйти из строя при этих перевозках. Пусть вероятность выхода из строя одной машины не зависит от выхода из строя других машин. Это значит, что рассматриваются независимые события (испытания). Вероятности выхода из строя каждой из этих машин примем одинаковыми ().

Пусть, в общем случае, производится 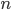независимых испытаний. Ставится задача определения вероятности того, что ровно в 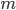испытаниях наступит событие 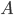, если вероятность наступления этого события в каждом испытании равна . В случае с машинами это могут быть вероятности выхода из строя ровно одной машины, ровно двух машин и т.д.

Определим вначале вероятность того, что в первых 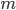испытаниях событие 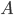наступит, а в остальных испытаниях — не наступит. Вероятность такого события может быть получена на основании формулы вероятности произведения независимых событий

,

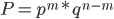где .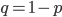

Так как рассматривалась только одна из возможных комбинаций, когда событие 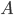произошло только в первых 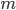испытаниях, то для определения искомой вероятности нужно перебрать все возможные комбинации. Их число будет равно числу сочетаний из 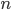элементов по 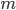, т.е. .

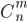Таким образом, вероятность того, что событие наступит ровно в испытаниях определяется по формуле

, (3.3)

где .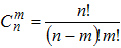

Формула (3.3) носит название формулы Бернулли.

13.Локальная теорема Лапласа.
Локальная теорема Лапласа

Пусть проводится n испытаний Бернулли с вероятностью р появления события А в

каждом из них.

Пусть при этом n достаточно большое число (n >> 1) и npq ≥ 10

(n – большое, а р – не очень маленькое)

Тогда вероятность, того, что событие А произойдет ровно k раз может быть найдена по

приближенной формуле: ,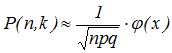

где: ,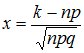

Замечание: таблица значений функции ϕ(х) обычно приводится в задачниках Теории вероятностей.

Свойства функции ϕ(x):

1. ϕ(х) > 0

2. ϕ(-х) = ϕ(х)

3. lim_{х стремится к бесконечности} ф (х)=0,(ф (ф)< 10^-4)

14.Интегральная теорема Лапласа.

Интегральная теорема Муавра-Лапласа. Пусть вероятность появления события А в каждом из n (n →∞)независимых испытаний равна одной и той же постоянной р (0< р <1), то вероятность 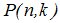того, что во всех этих испытаниях событие А появится не менее k ₁ и не более k ₂ раз, приближенно вычисляется формулой:

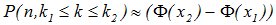, (4.9)

где

- функция Лапласа,

,

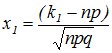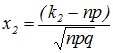
Значения аргументов функции Лапласа для х Î[0,5] даны в приложениях к учебникам по теории вероятностей (Приложение 2 настоящего методического пособия), для x>5 F(x)=1/2.Функция нечетная - F(x)= F(-x).

Дата добавления: 2015-04-24