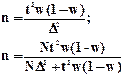Определение необходимой (оптимальной) численности выборки

Методы определения оптимальной численности выборочной совокупности.

При разработке программы выборочного обследования одним из наиболее сложных является вопрос о том, сколько единиц изу­чаемой совокупности необходимо обследовать, т.е. об объеме вы­борки.

При этом следует иметь в виду, что при любом способе отбора предельная ошибка выборки обратно пропорциональна числу обследованных единиц. Т.е. средняя ошибка выборки пропорциональна , т.е. при увеличении численности выборки в 4 раза, ошибка уменьшится вдвое. Увеличивая n можно свести ошибку к min. При n ® N, ®₀.

Так как при проведении выборочного наблюдения определение характеристик выборки в ряде случаев сопровождается разрушением обследуемых образцов, то нормы отбора должны быть минимальны, так же не следует забывать об основном преимуществе несплошного наблюдения (минимум затрат и времени). Повышение процента выборки ведет к увеличению объема исследуемой работы. В то же время, если в выборку взять недостаточное количество проб, то результаты исследования будут содержать большие погрешности. Все это необходимо учитывать при организации выборочного обследования.

Определение необходимой численности выборки основывается на формуле предельной ошибки выборки (при повторном отборе).

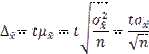
Решаем это равенство относительно n, в результате получаем численность выборки при расчете средней величины количественного признака.

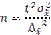
Для определения необходимой численности выборки должны быть заданы предельная ее ошибка и вероятность того, что эта ошибка не превысит заданного предела. В соответствии с этой вероятностью по таблице распределения находят коэффициент доверия t.

Наиболее сложно определить дисперсию изучаемого признака в генеральной совокупности. До проведения обследования приближенно оценить дисперсию или среднее квадратическое откло­нение можно на следующей основе:

1. исходя из результатов специально организованного пробного обследования;

2. опираясь на данные предыдущих обследований, как выборочных, так и сплошных.

Например, используя коэффициент вариации . Следовательно, дисперсия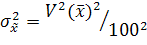

3. исходя из закона распределения изучаемого признака в гене­ральной совокупности. Если распределение близко к нормаль­ному, то размах вариации R в 6 раз больше среднего квадратического отклонения: R = 6s. В таком случае, зная максимальное и минимальное значения признака, можно оценить s: s=R/6

Если в результате выборочного обследования необходимо ус­тановить долю единиц, обладающих определенным значением альтернативного признака, то дисперсия для доли будет равна рq. В этом случае формула необходимой численности выборки при­мет вид:

Максимальное значение дисперсии альтернативного признака равно 0,25, т.е. max (pq) = 0,25 (при р = q -x*ользуя кямо ичество фаз, каждая из которых отличается подробностью программы наблюдениякими буквами, выборочные показатели, 0,5). Если доля единиц, обладающих изучаемым признаком, т.е. р, неизвестна, в расчете необходимой численности выборки можно использовать указанное максимальное значение для дисперсии альтернативного признака.

Трудовые и материальные затраты на проведение выборки напрямую зависят от ее численности, поэтому чрезвычайно важно до оптимума сохранить численность выборки, так чтобы не утратить ее точность.

Поиск оптимальной численности выборки удобно осуществлять на основе формул средней и предельной ошибок. Из формулы средней ошибки случайного повторного отбора видно, что величина средней ошибки обратно пропорциональна квадратному корню из численности выборки

()

Чтобы сократить среднюю ошибку в 2 раза, нужно численность выборки увеличить в 4 раза. Используя формулу предельной ошибки выборки можно найти численность

Это оптимальная численность выборки для случайного повторного отбора

Наличие в формуле оптимальной численности генеральной дисперсии приводит на первый взгляд к парадоксу: зачем нам проводить выборку, если известна генеральная дисперсия (а, следовательно, и генеральная средняя). Однако на практике генеральная дисперсия обычно не известна, вместо нее используют выборочную дисперсию предыдущего обследования, так как дисперсия как показатель является более устойчивой, чем сами варианты, на основе которых она рассчитана.

Если отбор осуществляется бесповторно, то численность выборки для такого отбора рассчитывается по формуле:

Если в условиях задачи присутствует предельная ошибка выборочной доли, то формула:

- для повторного отбора; - для бесповторного отбора.

Дата добавления: 2015-04-24