Решение краевой задачи для дифференциальных уравнений методом Галеркина

Общая схема метода Галеркина для решения уравнений

Метод Галёркина (метод Бубнова — Галёркина) — метод приближённого решения краевой задачи для дифференциального уравнения 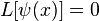. Здесь оператор 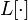может содержать частные или полные производные искомой функции.

Краевая задача — дифференциальное уравнение (система дифференциальных уравнений) с заданными линейными соотношениями между значениями искомых функций на начале и конце интервала интегрирования.

Решение краевой задачи ищется в виде линейной комбинации решений однородных задач Коши, соответствующих заданному уравнению при линейно независимых векторах начальных условий, и решения неоднородной задачи Коши с произвольными начальными условиями.

Пример краевой задачи:

Первым шагом в реализации метода Галёркина является выбор набора базисных функций, которые:

- удовлетворяют граничным условиям.

- в пределе бесконечного количества элементов базиса образуют полную систему.

Конкретный вид функций определяется из специфики задачи и удобства работы. Часто применяются тригонометрические функции, ортогональные полиномы (полиномы Лежандра, Чебышёва, Эрмита и др.).

Решение представляется в виде разложения по базису:

Затем приближённое решение подставляется в исходное дифференциальное уравнение, и вычисляется его невязка. Для однородного уравнения:

Для неоднородного уравнения L[u]=f(x) невязка будет иметь вид N(x)=L[u]-f(x)

Далее выдвигается требование ортогональности невязки к базисным функциям, то есть:

Отсюда получается однородная система уравнений для коэффициентов в разложении, и удаётся приближённо найти собственные значения задачи.

Рассмотрим в качестве иллюстрации обыкновенное дифференциальное уравнение:

с граничными условиями:

Решение данного уравнения известно:

Для первого нетривиального решения собственное число равно .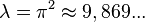

Теперь применим метод Галёркина. Выберем сперва одну базисную функцию:

Подставляя в уравнение, получим невязку:

и требование ортогональности невязки перепишется в виде:

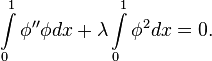
Отсюда очевидно:

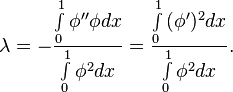
В приводимом здесь примере получается 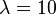, что менее чем на 1,5 % отличается от точного решения. Задание большего числа базисных функций позволяет уточнить уже известное значение λ, а также получить первое приближение для следующего (соответствующего n=2).

Представим решение в виде линейной комбинации n функций:

Тогда невязка:

.

Система уравнений для коэффициентов разложения:

В этом случае собственные значения находятся из условия разрешимости системы (равенство нулю её определителя):

Важно помнить, что сходимость метода Галёркина не всегда быстро достигается. Успешное применение возможно только для т. н. самосопряжённых задач, то есть инвариантных к эрмитовому сопряжению.

Дата добавления: 2015-04-24