Случай вырожденных ядер

Ядро K(x,t), представимое конечной суммой вида 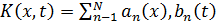, называется вырожденным ядром. Здесь функции 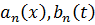, n = 1,2,...,N будем считать непрерывными в квадрате a ≤ x, t≤b и линейно-независимыми между собой.

Рассмотрим интегральное уравнение с вырожденным ядром 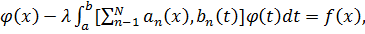или 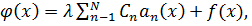(9) где 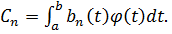Подставим 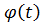в виде суммы (9) в последнее соотношение. Получим 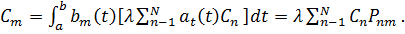(10)

В результате мы пришли к системе однородных алгебраических уравнений (10) относительно . Нас интересует нетривиальное решение системы (10). Последнее возможно, если 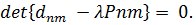Это соотношение является алгебраическим уравнением N -й степени относительно . Отсюда следует утверждение: вырожденное ядро имеет конечное число собственных значений.

35. Ряд Фурье по тригонометрической системе на симметричных отрезках

Ряд вида называется тригонометрическим рядом.

Пусть периодическая с периодом π2 функция f (x)представлена тригонометрическим рядом, сходящимся к данной функции на [− π; π], т. е. является суммой этого ряда

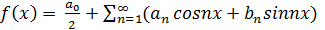(2)

f (x) разлагается в тригонометрический ряд равномерно.

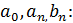
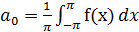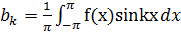Предположим, что этот ряд сходится на [− π; π]. Найдем его коэффициенты (3), (4), (5).

Таким образом, eсли периодическая функция f(x) с периодом 2π является суммой равномерно сходящегося на [− π; π] тригонометрического ряда, то коэффициенты этого ряда определяются по формулам:

Коэффициенты ряда (2), определенные по формулам (3), (4) и (5) называются коэффициентами Фурье (или коэффициентами Эйлера-Фурье), а тригонометрический ряд (2) с такими коэффициентами называется рядом Фурье функции f (x).

Если функция f (x) задана на сегменте [-l;l], где – произвольное число, то при выполнении на этом отрезке условий Дирихле указанная функция может быть представлена в виде суммы ряда Фурье:

где , .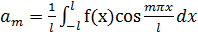

Формулу легко вывести, если сделать линейную замену независимой переменной Если , то 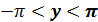. В результате функция ⎛=π определена на интервале (− π; π), и мы можем разложить её в ряд Фурье.

В случае, когда – четная функция, то ряд Фурье содержит только свободный член и косинусы, когда – нечетная, ее ряд Фурье содержит только синус.

Дата добавления: 2015-04-24