Векторное произведение векторов, определение, свойства

Свойства скалярного произведения

Скалярное произведение векторов, определение, свойства

Линейные операции над векторами.

Векторы, основные понятия, определения, линейные операции над ними

Вектором на плоскости называется упорядоченная пара ее точек, при этом первая точка называется началом, а вторая концом – вектора

Два вектора называются равными если они равны и сонаправлены.

Векторы, лежащие на одной прямой, называются сонаправленными если они сонаправленны с некоторым одним и тем же вектором, не лежащим на этой прямой.

Векторы, лежащие на одной прямой или на параллельных прямых называются коллинеарными, а коллинеарные но не сонаправленные – противоположно-направленные.

Векторы, лежащие на перпендикулярных прямых, называются ортогональными.

Определение 5.4. Суммой a + b векторов a и b называется вектор, идущий из начала вектора а в конец вектора b, если начало вектора b совпадает с концом вектора а.

Определение 5.5. Разностью а – b векторов а и b называется такой вектор с, который в сумме с вектором b дает вектор а.

Определение 5.6. Произведением k a вектора а на число k называется вектор b, коллинеарный вектору а, имеющий модуль, равный | k || a |, и направление, совпадающее с направлением а при k >0 и противоположное а при k<0.

Свойства умножения вектора на число:

Свойство 1. k( a + b ) = k a + k b.

Свойство 2. (k + m) a = k a + m a.

Свойство 3. k(m a) = (km) a.

Следствие. Если ненулевые векторы а и b коллинеарны, то существует такое число k, что b = k a.

Скалярным произведением двух ненулевых векторов a и b называется число (скаляр), равный произведению длин этих векторов на косинус угла φ между ними. Скалярное произведение можно обозначать различными способами, например, как ab, a · b, (a, b), (a · b). Таким образом, скалярное произведение равно:

a · b = | a | · | b | · cos φ

Если хотя бы один из векторов равен нулю, то скалярное произведение равно нулю.

· Свойство перестановки: a · b = b · a (от перестановки множителей скалярное произведение не меняется);

· Свойство распределения: a · (b · c) = (a · b) · c (результат не зависит от порядка умножения);

· Свойство сочетания (по отношению к скалярному множителю): (λ a) · b = λ (a · b).

· Свойство ортогональности (перпендикулярности): если вектора a и b ненулевые, то их скалярное произведение равно нулю, только когда эти векторы ортогональны (перпендикулярные друг к другу) a _┴ b;

· Свойство квадрата: a · a = a ² = | a |² (скалярное произведения вектора самого с собой равняется квадрату его модуля);

· Если координаты векторов a ={x₁, y₁, z₁} и b ={x₂, y₂, z₂}, то скалярное произведение равно a · b = x₁x₂ + y₁y₂ + z₁z₂.

Векторное проведение векторов. Определение: Под векторным произведением двух векторов 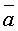и 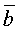понимается вектор, 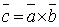для которого:

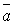-модуль равен площади параллелограмма, построенного на данных векторах, т.е. , где угол между векторами и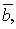

-этот вектор перпендикулярен перемножаемым векторам, т.е.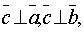

-если векторы неколлинеарны, то они образуют правую тройку векторов.

Свойства векторного произведения:

1.При изменении порядка сомножителей векторное произведение меняет свой знак на обратный, сохраняя модуль, т.е.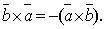

2. Векторный квадрат равен нуль-вектору, т.е.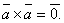

3. Скалярный множитель можно выносить за знак векторного произведения, т.е.

4. Для любых трех векторов 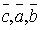справедливо равенство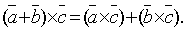

5. Необходимое и достаточное условие коллинеарности двух векторов 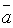и :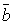

Дата добавления: 2015-04-24