
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Понятие вектора в абстрактной алгебре
Пусть  — некоторое поле с аддитивной операцией +, мультипликативной операцией *, аддитивной единицей 0 и мультипликативной единицей 1. Пусть
— некоторое поле с аддитивной операцией +, мультипликативной операцией *, аддитивной единицей 0 и мультипликативной единицей 1. Пусть 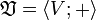 — некоторая абелева группа с единицей
— некоторая абелева группа с единицей 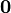 . Если существует операция
. Если существует операция 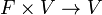 , такая что для любых
, такая что для любых  и для любых
и для любых  выполняются соотношения:
выполняются соотношения:
1.  ,
,
2. 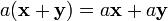 ,
,
3. 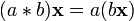 ,
,
4. 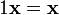 ,
,
тогда  называется векторным пространством над полем
называется векторным пространством над полем  , элементы V называются векторами, элементы F — скалярами, а указанная операция
, элементы V называются векторами, элементы F — скалярами, а указанная операция 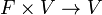 — умножением вектора на скаляр.
— умножением вектора на скаляр.
[править]Понятие вектора в стандартном евклидовом n-мерном пространстве
Вектор в арифметическом n-мерном пространстве
Является частным случаем определения вектора в абстрактной алгебре. Если в качестве 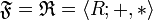 взять поле действительных чисел с операциями сложения и умножения.
взять поле действительных чисел с операциями сложения и умножения. 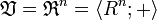 , где Rn — декартова степень множества R; для
, где Rn — декартова степень множества R; для  операцию «+» зададим следующим образом: (a 1,..., an) + (b 1,..., bn) = (a 1 + b 1,..., an + bn), нейтральный элемент:
операцию «+» зададим следующим образом: (a 1,..., an) + (b 1,..., bn) = (a 1 + b 1,..., an + bn), нейтральный элемент: 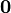 =(0,…,0), обратный элемент: − (a 1,..., an) = (− a 1,..., − an); операцию умножения на скаляр: a (a 1,..., an) = (a * a 1,..., a * an). Тогда вектор, задаваемый кортежем длиной n, состоящим из действительных чисел является арифметическим вектором векторного пространства
=(0,…,0), обратный элемент: − (a 1,..., an) = (− a 1,..., − an); операцию умножения на скаляр: a (a 1,..., an) = (a * a 1,..., a * an). Тогда вектор, задаваемый кортежем длиной n, состоящим из действительных чисел является арифметическим вектором векторного пространства  над полем действительных чисел
над полем действительных чисел 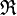 .
.
n-мерное пространство задается как Rn — декартова степень множества действительных чисел, точка -как кортеж (a 1,..., an) длины n из действительных чисел, что соответствует определению пространства как множества точек.
Вектор в геометрии(связанный вектор) — упорядоченная пара точек, одна из которых называется началом, вторая — концом вектора.
Два вектора равны, если разности по каждой из координат с одинаковыми номерами конечной и начальной точки для этих векторов равны. Эти разности называются пространственными координатами вектора.
Свободный вектор задается классом всех равных связанных векторов и полагается равным каждому из этих связанных векторов и таким образом может быть определен как вектор в арифметическом пространстве (кортеж чисел длины n (пространственных координат равных ему связанных векторов) с операциями сложения и умножения на скаляр).
Результатом операций со связанными векторами принимается вектор, начальная точка которого совпадает с начальной точкой первого слагаемого при сложении векторов и начальной точке исходного вектора при умножении вектора на скаляр.
Нуль-вектор - вектор, начало и конец которого совпадают.
Также существует более распространенное определение вектора как направленного отрезка, но оно требует определения прямой и отрезка в n-мерном пространстве.
Прямая, на которой лежит ненулевой вектор  с началом в точке M 0 = (m 1,..., mn), заданный свободным вектором с пространственными координатами (a 1,..., an) — множество точек (x 1,..., xn), удовлетворяющее условию:
с началом в точке M 0 = (m 1,..., mn), заданный свободным вектором с пространственными координатами (a 1,..., an) — множество точек (x 1,..., xn), удовлетворяющее условию:

Отрезок MN — множество всех точек O(удовлетворяющих условию  ), все различные точки которого принадлежат одной прямой, точки M и N называются концевыми точками отрезка. Отрезок называется направленным, если его концевые точки упорядочены. Если концы отрезка совпадают, он состоит из 1 точки.
), все различные точки которого принадлежат одной прямой, точки M и N называются концевыми точками отрезка. Отрезок называется направленным, если его концевые точки упорядочены. Если концы отрезка совпадают, он состоит из 1 точки.
При введение скалярного произведения, угла и длины вектора, задающей расстояние между двумя точками как расстояние между начальной и конечной точками вектора(как показано ниже([1], [2], [3])) векторное пространство Rn становится евклидовым нормированным пространством и при n=3 соответствует модели физического трехмерного пространства; при n=2 — плоскости этого пространства; при n=1 точка соответствует числу на числовой прямой, свободный вектор — разности двух чисел, а длина вектора соответствует модулю; при n=0 существует только одна точка(задается пустым кортежем), декартово произведение содержит только пустой кортеж, соответственно пространство представляет собой точку, есть только нулевой вектор; пространство при n>3 не имеет наглядной геометрической интерпретации, так как физическое пространство трехмерно.
Скалярное произведение определяется по формуле:  , [1]
, [1]
(где ai, bi — пространственные координаты векторов  )
)
Длина вектора: 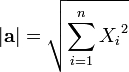 , [2]
, [2]
(где Xi — пространственные координаты вектора.)
Угол между 2-мя векторами  (где ai, bi — пространственные координаты векторов
(где ai, bi — пространственные координаты векторов  ) определяется через скалярное произведение:
) определяется через скалярное произведение:
 , [3]
, [3]
[править]Вектор в линейном пространстве
Линейное пространство — это множество элементов, называемых векторами, над которыми определённым образом определены операции сложения и умножения на число. В любом линейном пространстве можно выделить особую систему векторов, называемых базисом линейного пространства. Количество векторов в базисе равно размерности пространства. Любой вектор из пространства можно представить, как линейную комбинацию базисных векторов. То есть, если у нас есть базис  , то
, то 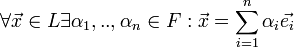 , где F — это поле, над которым определенно линейное пространство L.
, где F — это поле, над которым определенно линейное пространство L.
Выбор базиса в линейном пространстве неоднозначен, однако коэффициенты векторов при измерении базиса связанны определённым образом. Пусть есть базис 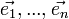 и
и  . Причём:
. Причём: 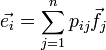 . Матрица Pef, полученная из коэффициентов pij называться матрицей перехода от базиса e а базису f и связывает координаты вектора в различных базисах следующем образом:
. Матрица Pef, полученная из коэффициентов pij называться матрицей перехода от базиса e а базису f и связывает координаты вектора в различных базисах следующем образом: 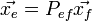 . Связь между матрицами перехода между двумя базисами:
. Связь между матрицами перехода между двумя базисами: 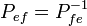 . Вектора могут иметь различную природу: направленные отрезки, матрицы, числа, функции и другие, однако все линейные пространства одной размерности изоморфны между собой.
. Вектора могут иметь различную природу: направленные отрезки, матрицы, числа, функции и другие, однако все линейные пространства одной размерности изоморфны между собой.
[править]Операции над векторами
Пусть в линейном пространстве выбран базис  и в нём представлены вектора вектора
и в нём представлены вектора вектора  ,
,  , тогда суммой векторов
, тогда суммой векторов  будет называется следующий вектор:
будет называется следующий вектор: 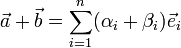 .
.
Пусть есть число λ, тогда произведением вектора  на число λ будет называться следующий вектор:
на число λ будет называться следующий вектор: 
Два ненулевых вектора  и
и  называются коллинеарными, если
называются коллинеарными, если  .
.
[править]Евклидовы и нормированные пространства
Основная статья: Евклидово пространство
Основная статья: Нормированное пространство
Функция  (в другом обозначении
(в другом обозначении 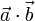 ), ставящая любым двум векторам
), ставящая любым двум векторам  в соответствие число и удовлетворяющая следующим аксиомам:
в соответствие число и удовлетворяющая следующим аксиомам:
1. Линейность по первому аргументу: 
2. Эрмитова симметричность:  (в случае если вектора определены над полем действительных чисел, то
(в случае если вектора определены над полем действительных чисел, то 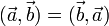 )
)
3. Положительная определённость:  тогда и только тогда, когда
тогда и только тогда, когда  ,
,
называется скалярным произведением вектора  на вектор
на вектор  . Конечномерное линейное пространство с введённым скалярным произведением называется евклидовым. Для пространств над полем комплексных чисел иногда применяют термин унитарное пространство.
. Конечномерное линейное пространство с введённым скалярным произведением называется евклидовым. Для пространств над полем комплексных чисел иногда применяют термин унитарное пространство.
Два не нулевых вектора  называются ортогональными, если
называются ортогональными, если 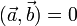 .
.
Базис  евклидова пространства называется ортогональным, если
евклидова пространства называется ортогональным, если 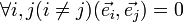 . Базис называется ортонормированным, если
. Базис называется ортонормированным, если  , где δ ij — символ Кронекера.
, где δ ij — символ Кронекера.
Скалярное произведение является билинейной формой, поэтому его можно записать в следующем виде:
 , где Ae — матрица Грамма.
, где Ae — матрица Грамма.
В случае ортонормированного базиса матрица будет единичной, и тогда, если  ,
,  , то
, то
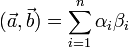 в случае действительного пространства и
в случае действительного пространства и  в случае комплексного.
в случае комплексного.
Так же в линейном пространстве можно ввести понятие нормы. Это функция, ставящая в соответствие любому вектору линейного пространства неотрицательное вещественное число и удовлетворяющая следующим аксиомам:
1. 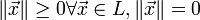 тогда и только тогда, когда
тогда и только тогда, когда  .
.
2.  .
.
3.  .
.
Угол ϕ между векторами  определяется, как
определяется, как 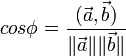
| ||
|
|
Дата добавления: 2015-04-24; Просмотров: 624; Нарушение авторских прав?; Мы поможем в написании вашей работы!
 Доказательство. Пусть AB и CD – одинаково направленные векторы, равные по абсолютной величине. Параллельный перенос, переводящий точку A` в точку A, совмещает луч A`B` с лучом AB, потому что они сонаправлены. Отрезка AB и A`B` равны, поэтому точка B совмещается с точкой B`. Значит, параллельный перенос переводит вектор A`B` в вектор AB. Значит векторы равны. Теорема доказана.
Доказательство. Пусть AB и CD – одинаково направленные векторы, равные по абсолютной величине. Параллельный перенос, переводящий точку A` в точку A, совмещает луч A`B` с лучом AB, потому что они сонаправлены. Отрезка AB и A`B` равны, поэтому точка B совмещается с точкой B`. Значит, параллельный перенос переводит вектор A`B` в вектор AB. Значит векторы равны. Теорема доказана.