Билет №21. Извлечение корня из комплексного числа в тригонометрической форме. Вывод формулы для нахождения корней степени n из единицы. Их расположение на комплексной плоскости

Билет №20. Возведение в степень с натуральным показателем комплексного числа в тригонометрической форме. Вывод формулы Муавра. Показательная форма комплексного числа. Умножение, деление, возведение в натуральную степень чисел в показательной форме.

Вопрос № 19. Модуль и аргумент комплексного числа. Тригонометрическая форма комплексного числа. Умножение и деление чисел в тригонометрической форме. Вывод формулы для произведения

Число 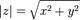называется модулем числа z. Для вещественного числа модуль совпадает с его абсолютной величиной.

Угол 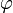такой, что: 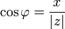и 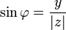, называется аргументом z. Для комплексного нуля значение аргумента не определено, для ненулевого числа z аргумент определяется с точностью до 2 k π, где k — любое целое число. Из определения следует, что .

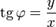Пусть 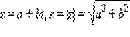и φ = arg z. Тогда по определению аргумента имеем:

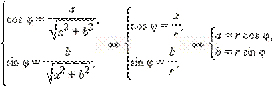
Получается

z = a + bi = r (cos φ + i sin φ).

Такая форма называется тригонометрической формой записи комплексного числа.

Умножение компл.чисел:

Пусть Z1 и Z2, Z1=(a1;b1), Z2=(a2;b2)

Z=z1∙z2⇒ { a=a1∙a2-b1∙b2

b=a1∙b2+a2∙b1

Формула Муавра для комплексных чисел 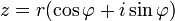, заданная в тригонометрической форме — формула

для любого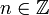

Аналогичная формула применима также и при вычислении корней n -ой степени из ненулевого комплексного числа:

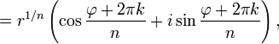
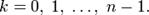
Если вещественную x и мнимую y части комплексного числа выразить через модуль r = | z | и аргумент 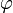(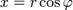, 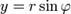), то всякое комплексное число z, кроме нуля, можно записать в тригонометрической форме

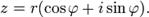
Также может быть полезна показательная форма записи комплексных чисел.

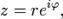
где 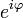— расширение экспоненты для случая комплексного показателя степени.

Отсюда вытекают следующие широко используемые равенства:

Число корней равно показателю степени.

Z1 = n√Z ↔ Z = Z1n

Корнем n-й степени (n ∊ N, n ≥ 2) из числа z называется любое комплексное число u, для которого un = z. Операция нахождения всех корней n-й степени из числа z называется извлечением корня.
Для нахождения всех корней n-й степени существует следующая формула:

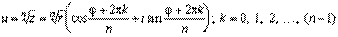
Формула для нахождения корней степени n из единицы

n√1={zk | zk= здесь та же формула, что и наверху (то, что в скобках), только без φ

Дата добавления: 2015-04-24