Метод Ньютона (метод касательных прямых) для уточнения изолированного корня алгебраического или трансцендентного уравнения

f(x)=0 (1)

пусть является корнем решения (1) этот корень отделен на отрезке 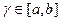причем не прерывна и сохраняет опред. знаки на отрезке [a,b] найдем какой-либо способ (n-е приближение) к корню.

Тогда точное решение уравнение (1) можно записать как существование некоторого приближения 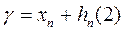уточним 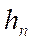так как функция f(x) не прерывна на отрезке [a,b], то с учетом равенства (2) можно записать к данному равенству применим формулу Тейлора:

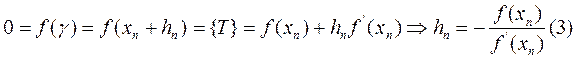
Тогда с учетом равенства (3)+(2) следует:

Геометрически это означает замену небольшой дуги кривой касательной проведенный к некоторой точке кривой по этому метод ньютона называют метод касательных.

Иллюстрация метода Ньютона (синим изображена функция , нуль которой необходимо найти, красным — касательная в точке очередного приближения 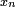). Здесь мы можем увидеть, что последующее приближение лучше предыдущего .

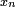Основная идея метода заключается в следующем: задаётся начальное приближение вблизи предположительного корня, после чего строится касательная к исследуемой функции в точке приближения, для которой находится пересечение с осью абсцисс. Эта точка и берётся в качестве следующего приближения. И так далее, пока не будет достигнута необходимая точность.

Пусть — определённая на отрезке и дифференцируемая. Тогда формула итеративного исчисления приближений может быть выведена следующим образом:

где — угол наклона касательной в точке .

Следовательно искомое выражение для 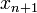имеет вид:

Если За взять 0, то точка будет лежать вне отрезка [a,b] за начальное приближение берется та точка значение функции в которой совпадает со значением второй производной этой функции в любой точки отрезка [a,b].

Дата добавления: 2015-04-24