Завдання на лабораторну роботу

Методи з регулюванням кроку (методи Ньютону-Рафсона).

Вдалий вибір початкового наближення x ₀ гарантує збіжність методу Ньютону. Однак відшукання вдалого початкового наближення — далеко не проста задача. Тому необхідно якось змінити формулу (4), щоб домогтися збіжності незалежно від початкового наближення. Доведено, що в деяких припущеннях для цього досить у методі Ньютону крім напрямку руху 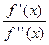обирають і довжину кроку вздовж нього. Такі алгоритми називаються методами Ньютону з регулюванням кроку (методами Ньютону-Рафсона) та виглядають так:

.

(8)

Як і в градієнтних методах величина a_k вибирається так, щоб забезпечити спадання цільової функції на кожній ітерації. Ми розглянемо два способи вибору кроку a_k. Перший з них пов'язаний з перевіркою нерівності

,

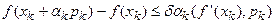(9)

де 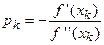— напрямок спуску, а 0< d <½ — деяке задане число, загальне для всіх ітерацій. Якщо ця нерівність виконується при a_k =1, то крок приймається рівним одиниці та виконується наступна ітерація. Якщо ні — ділиться доти, поки воно не виконається.

Алгоритм методу Ньютону-Рафсона з дробленням кроку.

Крок 1.

На першій ітерації, при k =0, задаються

x _0,

d,

ε _.

Обчислюються значення градієнта 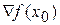і матриця .

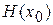Крок 2.

Привласнюється a =1. Визначається напрямок спуску p_k як розв'язання системи лінійних рівнянь .

Крок 3.

Перевіряється умова

.

Якщо виконується, то перехід до кроку 4.

Інакше дробимо значення кроку α (наприклад, α = α /2) і повторюємо крок 3.

Крок 4.

Визначається наступна точка:

.

~

~

Крок 5.

Обчислюються значення градієнта f '(x_{k +1}) в точці x_{k +1}.

Крок 6.

Якщо , то пошук на цьому закінчується й покладається

.

Інакше k = k +1 і перехід до кроку 2.

Другий метод визначення кроку a_k у схемі (6), як і в методі найшвидшого спуску полягає в мінімізації функції

a ≥ 0

.

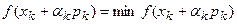
Алгоритм методу Ньютону-Рафсона з вибором оптимального кроку.

Крок 1.

При k =0, задаються

x ₀,

ε _.

Обчислюються f '(x ₀) і f ''(x ₀).

Крок 2.

Визначення напрямку спуску p_k, як розв'язання системи лінійних рівнянь .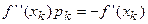

a≥ 0

Крок 3.

Визначається наступна точка спуску:

,

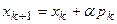де a — розв'язання задачі одномірної оптимізації: min f (x_k + ap_k).

Крок 4.

Обчислюються в точці x_{k +1}: f '(x_{k +1}) і f ''(x_{k +1}).

~

~

Крок 5.

Якщо , то пошук закінчується й покладається

.

Інакше k = k +1 і перехід до кроку 2.

1.2.3. Модифікації методу Ньютону

Значні труднощі, що виникають при практичній реалізації методу Ньютону, пов'язані з необхідністю обчислити матрицю f ''(x). Ми розглянемо дві модифікації методу Ньютону, які використовують не точні значення, а деякі наближені аналоги матриці других похідних. У результаті зменшується трудомісткість методів, але, звичайно, погіршується їхня збіжність.

Як перша модифікація методу Ньютону розглянемо наступний алгоритм:

,

(10)

тут для побудови напрямку спуска використовується один раз обчислена й звернена матриця других похідних f ''(x ₀).

Схема модифікації I методу Ньютону.

Крок 1.

При k =0, задаються

x ₀,

ε _.

Обчислюються f '(x ₀) і f ''(x ₀).

Крок 2.

Визначення зворотної матриці (f ''(x ₀))^–1.

Крок 3.

Визначення напрямку спуску p_k:

.

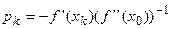Крок 4.

Визначення наступної точки:

,

де a — розв'язання задачі одномірної мінімізації функції

.

~

~

Крок 5.

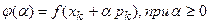Обчислення в точці x_{k +1}.градієнта f '(x_{k +1})

Крок 6.

Якщо , то пошук закінчується й покладається

.

Інакше k = k +1 і перехід до кроку 3.

У розглянутій схемі для вибору кроку a_k використовується спосіб аналогічний використовуваному в методі найшвидшого спуску. Але можна було б скористатися й способом аналогічним використовуваному в градієнтному методі з дробленням кроку.

Якщо матриця f ''(x) додатньо визначена, то ітераційний процес (d) є однією з модифікацій градієнтного спуску, незалежно від початкового наближення x ₀.

Інша модифікація методу Ньютону пов'язана з відновленням матриці других похідних через певну кількість кроків. Формула обчислення чергової точки x_{k +1}, у цьому випадку, буде мати наступний вигляд:

,

.

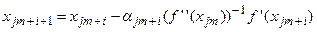Тут m >0 — ціле число, що визначає кількість кроків, через яке відбувається відновлення матриці других похідних f ''(x). Цей метод займає проміжне місце між методом Ньютону і його модифікацією I.

Схема модифікації II методу Ньютону.

Крок 1.

Задаються:

x ₀,

ε,

m.

Приймається j =0 і k =0.

Обчислюється градієнт f '(x ₀).

Крок 2.

Обчислюється (оновлюється) матриця f ''(x_jm) і обернена матриця .

Крок 3.

Визначення напрямку спуску p_{jm +1}:

.

Крок 4.

Визначення чергової точки x_{jm + i +1}:

,

де a — розв'язок задачі одномірної мінімізації функції

.

~

Крок 5.

Обчислення в черговій точці x_{jm + i +1}.градієнта f '(x_{jm + i +1})

Крок 6.

Якщо 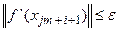, то пошук закінчується та приймається

.

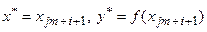Інакше k = k +1 і перехід до кроку 7.

Крок 7.

Визначається i = i +1.

Якщо i = m, то j = j +1, i =0 і перехід до кроку 2 (тобто оновлюється матриця f ''(x)).

Інакше перехід до кроку 3 (тобто використовується матриця f ''(x), обчислена на одному з попередніх кроків).

1. Вивчити всі викладені методи багатомірної безумовної оптимізації.

2. Запрограмувати методи оптимізації у відповідності зі своїм варіантом.

Кожен метод повинен бути оформлений у вигляді окремої функції, що викликається з головної функції програми.

Всі параметри методів (границі проміжку невизначеності, різні граничні значення, точність розв’язання, вказівник на цільову функцію тощо) мають передаватись як аргументи відповідних функцій.

Передбачити для користувача можливість вибору виводу на екран проміжних результатів процесу пошуку або виводу тільки кінцевої відповіді.

3. Порівняти результати, отримані різними методами для однієї й тієї ж цільової функції, зокрема, це можуть бути наступні результати:

a. кількість ітерацій, що знадобилась для досягнення заданої точності розв’язку;

b. число обчислень цільової функції та її похідних, що знадобилися для одержання заданої точності;

c. час виконання програм.

4. Для кожного застосованого методу побудувати траєкторію проміжних точок, одержуваних на чергових кроках методу й збіжних до точки мінімуму.

5. Оформити звіт про виконання завдання, що має містити:

a. умову задачі;

b. код програм зазначених у завданні методів оптимізації;

c. графіки траєкторій проміжних наближень;

d. таблиці результатів порівняння розглянутих методів;

e. висновок за результатами порівняння методів.

3. Варіанти завдань

Методи мінімізації:

1) метод Флетчера-Рівса;

2) метод мінімізації неквадратичної цільової функції.

3) метод Ньютону;

4) метод Ньютона-Рафсона із дробленням кроку;

5) метод Ньютона-Рафсона з оптимальним кроком;

6) модифікація I методу Ньютона;

7) модифікація II методу Ньютона;

Варіанти задач

Цільова функція

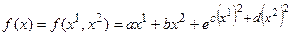
№	Цільова функція	Початкове наближення	ε
A	b	C	d
	1,0	-1,2	0,01	1,1	(0;1)	1·10^–4
	2,0	-1,3	0,04	1,2	(1;1)	2·10^–4
	3,0	-1,4	0,09	1,3	(-1;0)	3·10^–4
	10,0	-1,0	1,00	2,0	(0;0)	2·10^–4
	11,0	-0,9	1,21	2,1	(0;-1)	4·10^–4
	12,0	-0,8	1,44	2,2	(1;0)	3·10^–4
	16,0	-0,4	2,56	2,6	(1;1)	2·10^–4
	17,0	-0,3	2,89	2,7	(0;-1)	5·10^–4
	18,0	-0,2	3.24	2,8	(-1;0)	3·10^–4
	19,0	-0,1	3,81	2,9	(10;)	5·10^–4

Дата добавления: 2015-05-23