Інтерполювання сплайнами

Поліном лагранжа

Інтерполяційний многочлен Лагранжа

Побудуємо інтерполяційний многочлен Лагранжа L_n(x), який задовольняє умову (4.1).

Многочлен L_n(x) шукатимемо у вигляді лінійної комбінації спеціально сконструйованих многочленів степеня п:

.

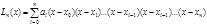Для визначення коефіцієнтів а_і (і =0,1,..., n), скористаємось вузловими умовами (4.2). Тоді шукані коефіцієнти визначаються як:

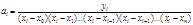
Підставивши знайдені коефіцієнти а_i, дістанемо вираз інтерполяційного многочлена L_n(x):

(4.4)

Інтерполяційний многочлен, записаний у вигляді (4.4), називається інтерполяційним многочленом Лагранжа.

Формулі Лагранжа (4.4) можна надати іншого вигляду:

,

де ,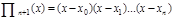

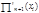- значення похідної від функції 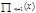у точці х=х_і.

Інтерполювання функцій за допомогою сплайнів

При інтерполюванні функцій з великою кількістю вузлів інтерполяційний поліном Лагранжа має високий степінь, що спричиняє коливання полінома на проміжках між вузлами інтерполювання. Щоб зменшити степінь інтерполяційного полінома вузли інтерполювання можна розбити на групи і будувати інтерполяційні поліноми з меншою кількістю вузлів. Але в цьому разі на стиках між вузлами порушуються аналітичні властивості інтерполяційного полінома, з'являються точки розриву похідних. Позбутися цих недоліків при інтерполюванні можна за допомогою так званих сплайнів. Наочне уявлення про сплайни дають криві, побудовані за допомогою лекал, а також трамвайні та залізничні колії. Найпростіший приклад сплайнів — ламані.

Більшість диференціальних рівнянь, котрі застосовуються для опису явищ природи та процесів в техніці і хімії, є рівняннями другого порядку. Для коректного відображення інтерпольованої функції в цих рівняннях має бути збережена нерозривність похідних першого і другого порядку. Тому з огляду на економію обчислювальних ресурсів і мінімізацію кількості екстремальних точок інтерполюючого полінома ці вимоги можна задовольнити лише в межах кубічних поліномів, котрі називають кубічними сплайнами, котрі, як доведено [7], є найкращими з функцій, які інтерполюють задану функцію.

Розглянемо задачу інтерполювання функції у=f(x) на відрізку [ a;b ] за допомогою кубічних сплайнів. Нехай на відрізку [ а; b ] задано сітку, у вузлах якої відомі значення у_i (і =1,2,..., п) функції f (x), визначеної на відрізку [ a;b ]. Будемо шукати функцію S(x), яка задовольняє вимоги:

1) на кожному з відрізків [ х_і; х_і+1 ], і =1,2,..., n -1 функція S(х) є кубічним поліномом:

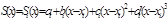
2) функція S (х) неперервна на [ а; b ] разом із своїми похідними до другого порядку включно, тобто

3) у вузлах х_і виконуються рівності

Функцію S(x), що задовольняє ці умови, називають інтерполяційним кубічним сплайном.

Для знаходження 4n-4 невідомих коефіцієнтів сплайна маємо 4n - 6 рівнянь (умови 2, 3). Для коректності не вистачає двох рівнянь, які можна одержати з крайових умов: S"(x₁) = S"(x_п) = 0. Це означає, що на кінцях відрізка інтерполювання сплайн S(x) буде мати нульову кривину. Слід зауважити, що вибір крайових умов можна здійснити й інакше. Зазначимо, що складена система лінійних рівнянь завжди має розв’язок, тобто кубічний сплайн існує для будь-якого набору вузлових точок, що не співпадають.

Задача інтерполювання кубічним сплайном розв’язана і запрограмована в межах практично всіх доступних програмних пакетів.

16) Метод найменших квадратів

Суть методу найменших квадратів Гауса

У процесі вивчення різних питань природознавства, економіки і техніки, соціології, педагогіки доводиться на основі великої кількості дослідних даних виявляти суттєві фактори, які впливають на досліджуваний об’єкт, а також встановлювати форму зв’язку між різними зв’язаними одна з одною величинами (ознаками).

Нехай у результаті досліджень дістали таблицю деякої функціональної залежності. Ставиться задача знайти аналітичний вигляд залежності, яка добре відображає цю таблицю дослідних даних.

Оскільки значення функції у_і дістають у результаті експерименту, а вони, як правило, сумнівні, то задача інтерполювання табличної функції втрачає сенс. Тому шукають таку функцію у=F(x), значення якої при х=х_і досить близькі до табличних значень у_і (і =1,2,…, n). Знайдену функцію у=F(x) називають емпіричною або рівнянням регресії у на х.

Емпіричні формули мають велике практичне значення: вдало підібрана емпірична формула дає змогу не тільки апроксимувати сукупність експериментальних даних, «згладжуючи» значення величини у, а й екстраполювати знайдену залежність на інші проміжки значень х.

Процес побудови емпіричних формул складається з двох етапів:

1) встановлення загального виду цієї формули;

2) визначення найкращих її параметрів.

Щоб встановити вигляд емпіричної формули, на площині будують точки з координатами (х_і, у_і) (і =1,2,..., n). Деякі з цих точок сполучають плавною кривою, яку проводять так, щоб вона проходила якомога ближче до всіх даних точок. Після цього візуально визначають, графік якої з відомих функцій найкраще підходить до побудованої кривої. Звичайно, намагаються підібрати найпростіші функції: лінійну, квадратичну, дробово-раціональну, степеневу, показникову, логарифмічну.

Встановивши вигляд емпіричної формули, треба знайти її параметри (коефіцієнти). Найточніші значення коефіцієнтів емпіричної формули визначають за методом найменших квадратів. Цей метод запропонували відомі математики К.Гаус і А.Лежандр.

Нехай емпірична формула має вигляд

y=F(x; a₁,a₂,…, a_k),

де a₁,a₂,…, a_k – невідомі коефіцієнти. Треба знайти такі значення коефіцієнтів а_і (і =1,2,..., k), за яких крива якомога ближче проходитиме до всіх точок (х₁,у₁), (х₂, у₂) …,(x_n, y_n), знайдених експериментально, причому n ≥ k. Зрозуміло, що кожна з експериментальних точок може не задовольняти точно знайдене рівняння (рис.5.1).

Рис.5.1.

Відхилення (нев’язки) від підстановки координат (х_і, у_і) у рівняння дорівнюватимуть величинам

δ_і = у_і - F(x; a₁,a₂,…, a_k), (і=1,2,...,n).

За методом найменших квадратів найкращі значення коефіцієнтів a₁,a₂,…, a_k ті, для яких сума квадратів відхилень дослідних даних y_i від обчислених за емпіричною формулою найменша.

Звідси випливає, що функція

S(a₁,a₂,…, a_k) = ,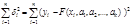

яка є функцією від коефіцієнтів a₁,a₂,…, a_k, неперервна і обмежена знизу, тому за теоремою Вейєрштраса має мінімум.

Необхідною умовою існування мінімуму функції багатьох змінних в точці є одночасна рівність нулю її частинних похідних, тобто

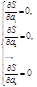
Для функції S(a₁,a₂,…, a_k) невідомі параметри a₁, a₂, …, a_k є змінними величинами, тому продиференціюємо її за невідомими параметрами a₁, a₂, …, a_k іматимемо відносно них систему рівнянь:

Якщо емпірична функція лінійна відносно параметрів a₁, a₂, …, a_n, то система буде складатися із n лінійних рівнянь відносно шуканих n параметрів. Якщо вона має єдиний розв’язок, то він і визначає шукану функцію найліпшого наближення.

Дата добавления: 2015-05-23