
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Приклади розв’язання задач
Приклад 1. Знайти за допомогою графічного методу розв’язок ЗЛП

Розв’язання. Побудуємо декартову систему координат, де вісь абсцис візьмемо за вісь  , а вісь ординат – за вісь
, а вісь ординат – за вісь  Як відомо з елементарної геометрії, лінійна нерівність
Як відомо з елементарної геометрії, лінійна нерівність  описує точки півплощини, які лежать по одну сторону від прямої
описує точки півплощини, які лежать по одну сторону від прямої  .
.
Таким чином, нерівності (1) – (3) описують півплощини, а їх сукупність – перетин півплощин.
Для визначення кожної півплощини спочатку будуємо пряму  і знаходимо нормальний вектор n
і знаходимо нормальний вектор n  . Він вказує на ту півплощину, точки якої задовольняють нерівність з відношенням “
. Він вказує на ту півплощину, точки якої задовольняють нерівність з відношенням “  ”. Для нерівності з відношенням “
”. Для нерівності з відношенням “  ” беремо півплощину, протилежну напрямку вектора n.
” беремо півплощину, протилежну напрямку вектора n.
Побудувавши прямі  ,
, 
 , що відповідають нерівностям (1)–(3), взявши відповідні півплощини і врахувавши умову невід’ємності змінних
, що відповідають нерівностям (1)–(3), взявши відповідні півплощини і врахувавши умову невід’ємності змінних 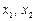 , маємо множину точок, що задовольняють усі обмеження задачі. Многокутник
, маємо множину точок, що задовольняють усі обмеження задачі. Многокутник  - область допустимих розв’язків або многокутник розв’язків (рис. 2.1).
- область допустимих розв’язків або многокутник розв’язків (рис. 2.1).
Будуємо на площині О  нормальний вектор функції N
нормальний вектор функції N  , координатами якого є коефіцієнти цільової функції. Він вказує напрямок, у якому функція
, координатами якого є коефіцієнти цільової функції. Він вказує напрямок, у якому функція  буде збільшуватися, у протилежному напрямку функція буде зменшуватися.
буде збільшуватися, у протилежному напрямку функція буде зменшуватися.
 |
Рис. 2.1
Оптимального плану досягаємо переміщенням лінії рівних значень  , яка перпендикулярна до вектора N
, яка перпендикулярна до вектора N  , паралельно самій собі у напрямку вектора N
, паралельно самій собі у напрямку вектора N  , оскільки потребується максимізація цієї функції. Переміщувати пряму можна доти, поки вона ще має спільні точки з областю. Таким чином, досягнемо положення прямої, що проходить через точку С. Визначаємо координати точки С. Для цього розв’язуємо систему, що складається з рівняння (1) і рівняння осі О
, оскільки потребується максимізація цієї функції. Переміщувати пряму можна доти, поки вона ще має спільні точки з областю. Таким чином, досягнемо положення прямої, що проходить через точку С. Визначаємо координати точки С. Для цього розв’язуємо систему, що складається з рівняння (1) і рівняння осі О  :
:

Розв’язавши систему, маємо точку С (14,0).
У цій точці спостерігаємо максимальне значення цільової функції  .
.
Відповідь: Оптимальний розв`язок: 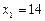 ,
, 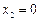 , максимальне значення цільової функції
, максимальне значення цільової функції 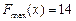 .
.
Приклад 2. Знайти оптимальний план задачі ЛП симплекс-методом.


 .
.
Розв’язання. Така задача була раніше розв’язана графічним методом (приклад 1). Розв’яжемо тепер цю задачу симплекс-методом. Запишемо задачу в стандартному вигляді (цільова функція прямує до мінімуму, обмеження – нерівності мають знак « ») і перенесемо вільні члени нерівностей в ліву частину:
») і перенесемо вільні члени нерівностей в ліву частину:


 .
.
Введемо додаткові змінні 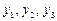 :
:

Складемо симплекс-таблицю (табл. 1) і знайдемо спочатку допустимий розв’язок. Для цього виконуємо послідовні перетворення, керуючись правилом 1. Серед відношень –24/4 та –24/6 вибираємо найменше. Додатний елемент, що утворив це відношення, обираємо за ведучий.
Таблиця 1

| 
| ||

| –1 | –2 | |
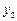
| –3 | ||
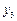
|  4 4
| –24 | |
| – F | –1 | –1 |
Після перетворень отримуємо табл. 2.
Таблиця 2
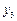
| 
| ||

| –1 | –2 | |

| –42 | ||

| –6 | ||
| – F | –1 | –24 |
Поділимо всі елементи табл. 2 на ведучий елемент та дістанемо табл. 3.
Таблиця 3
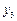
| 
| ||

|  –1/4 –1/4
| –1/2 | |

| 5/4 | –21/2 | |

| 1/4 | –3/2 | |
| – F | –1/4 | 1/2 | –6 |
Змінивши склад базисних і вільних змінних, ми досягли невід’ємності вільних членів (увійшли в допустиму область: ми знаходимось у точці (6;0), а це вже точка області), тобто допустимий план знайдено.
Оптимальним є план, в якому в симплекс-таблиці всі оцінки функції F(x) невід’ємні. Згідно з правилом 2 у табл. 3 вибираємо найбільше відношення невід’ємного вільного члена до від’ємного елемента в стовпчику з від’ємною оцінкою. Але таке відношення одне 8/(–1/4). Елемент (–1/4), що утворив це відношення, беремо за ведучий. Виконуємо перетворення і отримаємо табл. 4.
Таблиця 4

| 
| ||
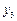
| 1/2 | –8 | |

| 5/4 | –26/8 | –85/4 |

| 1/4 | 4/8 | –14/4 |
| – F | –1/4 | –2/8 | 14/4 |
Поділимо всі елементи табл. 4 на ведучий елемент (–1/4) та дістаємо табл. 5.
Таблиця 5

| 
| ||
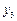
| –4 | –2 | |

| –5 | –13 | |

| –1 | –2 | |
| – F | –14 |
Оскільки в симплекс-таблиці (табл. 5) всі оцінки додатні, то план є оптимальним (п. 5.4). У цьому плані
 = 14,
= 14,  = 0,
= 0,  =0,
=0,  = 85,
= 85, 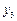 =32,
=32,
–  = –14 =>
= –14 =>  = 14.
= 14.
Під час розв’язування цієї задачі графічним методом, отримали такий самий оптимальний розв’язок  = 14,
= 14,  =0, при якому
=0, при якому  =14.
=14.
Відповідь: Оптимальний план:  =14,
=14,  =0,
=0,  =14.
=14.
Приклад 3. Знайти оптимальний план перевезень ТЗ, якщо аі = (180; 350; 20); bj = (110; 90; 120; 80; 150),
 .
.
Розв’язання. Задача закритого типу. Опорний план знайдемо методом північно-західного кута (табл. 4).
Таблиця 4

| 
| 
| 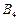
| 
| Запаси | |

| ||||||

| ||||||

| ||||||
| Заяви |
Опорний план:

Кількість базисних ненульових змінних дорівнює m+n –1=7, отже, опорний план невироджений.
Методом потенціалів знайдемо оптимальний план. Призначимо платежі  і
і  і занесемо в останній стовпчик і в останній рядок транспортної табл. 5.
і занесемо в останній стовпчик і в останній рядок транспортної табл. 5.
Знайдемо псевдовартості  для вільних клітин і занесемо їх у верхні ліві кути кожної вільної клітини табл. 5. Якщо для вільних клітин виконується умова
для вільних клітин і занесемо їх у верхні ліві кути кожної вільної клітини табл. 5. Якщо для вільних клітин виконується умова 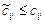 , то отриманий план оптимальний, якщо
, то отриманий план оптимальний, якщо  , то продовжуємо вдосконалювати опорний план.
, то продовжуємо вдосконалювати опорний план.
Таблиця 5

| 
| 
| 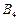
| 
| 
| |

| 70 – | 10 4 + | 9 8 | 7 5 | ||

| 3 1 | 20 + | 120 – | –4 | ||

| 4 6 | 9 13 | 7 8 | 6 7 | –3 | |

|
З табл. 5 видно, що план не є оптимальним, оскільки існують вільні клітини (1,3), (1,4), (1,5), (2,1), для яких  .
.
Для поліпшення плану для однієї з вище зазначених клітин побудуємо цикл. Візьмемо, наприклад, клітину (1,3). Цикл буде проходити по клітинах (1,3), (2,3), (2,2), (1,2). Починаючи з клітини (1,3) розставляємо почергово знаки «+» і «-». Визначаємо величину W – найменше перевезення в “мінусових” клітинах:  . Знайдену величину
. Знайдену величину 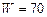 додаємо до перевезень у “плюсових” клітинах і віднімаємо від перевезень у “мінусових” клітинах. Базисна клітина (1,2), в якій знаходилася величина
додаємо до перевезень у “плюсових” клітинах і віднімаємо від перевезень у “мінусових” клітинах. Базисна клітина (1,2), в якій знаходилася величина 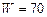 , стає вільною, а вільна клітина (1,3), для якої будували цикл, стає базисною. Новий опорний план наведено в табл. 6. Для одержання вартості нового плану визначаємо ціну циклу:
, стає вільною, а вільна клітина (1,3), для якої будували цикл, стає базисною. Новий опорний план наведено в табл. 6. Для одержання вартості нового плану визначаємо ціну циклу: 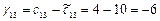 .
.
Вартість нового опорного плану буде становити:
 .
.
Таблиця 6

| 
| 
| 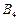
| 
| 
| |

| 110 – | 6 12 | 70 + | 3 8 | 1 5 | |

| 9 1 + | 50 – | ||||

| 1 6 | 9 13 | 7 8 | 6 7 | ||

|
Перевіряємо новий опорний план на оптимальність. Для цього знову призначаємо платежі  і
і  та визначаємо псевдовартості для вільних клітин. Для клітини (2;1) не виконується умова
та визначаємо псевдовартості для вільних клітин. Для клітини (2;1) не виконується умова 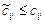 : 9>1, тому для вдосконалення плану для цієї клітини будуємо цикл. Клітини, пов’язані циклом, такі: (2,1), (1,1), (1,3), (2,3). Визначаємо величину W – найменше перевезення в “мінусових” клітинах:
: 9>1, тому для вдосконалення плану для цієї клітини будуємо цикл. Клітини, пов’язані циклом, такі: (2,1), (1,1), (1,3), (2,3). Визначаємо величину W – найменше перевезення в “мінусових” клітинах:  . Знайдену величину
. Знайдену величину  додаємо до перевезень у “плюсових” клітинах і віднімаємо від перевезень у “мінусових” клітинах. Базисна клітина (2,1), в якій знаходилася величина
додаємо до перевезень у “плюсових” клітинах і віднімаємо від перевезень у “мінусових” клітинах. Базисна клітина (2,1), в якій знаходилася величина  , стає вільною, а вільна клітина (2,3), для якої будували цикл, стає базисною. Новий опорний план наведено в табл. 7. Для одержання вартості нового плану визначаємо ціну циклу:
, стає вільною, а вільна клітина (2,3), для якої будували цикл, стає базисною. Новий опорний план наведено в табл. 7. Для одержання вартості нового плану визначаємо ціну циклу:  .
.
Вартість нового опорного плану буде становити:
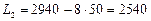 .
.
Таблиця 7

| 
| 
| 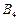
| 
| 
| |

| 60 – | 14 12 | 11 8 + | 3 5 | ||

| 50 + | –2 6 | 80 – | –6 | ||

| 2 6 | 9 13 | –1 8 | 6 7 | –5 | |

|
Знайдений план не є оптимальним. Подальший розв’язок задачі наведено в табл. 8 і 9.
 ,
,  ,
,
 .
.
Таблиця 8

| 
| 
| 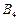
| 
| 
| |

| 4 7 | 11 12 | 60 – | 6 5 + | ||

| 1 6 | 20 + | 130 – | –3 | ||

| 2 6 | 9 13 | 2 8 | 6 7 | –2 | |

|
 ,
, 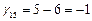 ,
,
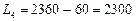 .
.
Таблиця 9

| 
| 
| 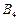
| 
| 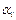
| |

| 3 7 | 10 12 | 7 8 | |||

| 2 6 | –2 | ||||

| 2 6 | 9 13 | 3 8 | 6 7 | –1 | |

|
Наведений в табл. 9 план є оптимальним, оскільки виконується ознака оптимальності.
Відповідь: 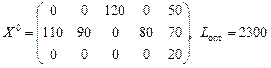 .
.
|
|
Дата добавления: 2015-05-23; Просмотров: 500; Нарушение авторских прав?; Мы поможем в написании вашей работы!