Уравнения Лагранжа первого рода

В данном разделе, не вдаваясь в подробное обоснование, мы сформулируем принцип Даламбера-Лагранжа, и выведем уравнения Лагранжа первого рода для механических систем с односторонними связями. В локальной формулировке принцип Даламбера-Лагранжа для таких систем известен уже давно [7]. Однако, исходя из него, затруднительно получать уравнения движения справедливые на всем отрезке движения, поскольку в его формулировке присутствуют ускорения точек системы, которые могут быть неопределенными в моменты выхода на границу односторонних связей (т.е. в точках удара). В данном разделе мы даём интегральную формулировку принципа Даламбера-Лагранжа, которая позволяет избавиться от этих трудностей.

Рассмотрим механическую систему с линейными удерживающими связями (7.3). Добавим к ним семейство односторонних голономных связей

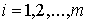, (8.1)

Конфигурационное пространство. Множество точек , удовлетворяющих связям (7.3, 8.1) будем называть расширенным конфигурационным пространством или, иногда, для краткости просто конфигурационным пространством. Внутренностью конфигурационного пространства будем называть множество точек , в которых

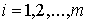, (8.2)

Границей конфигурационного пространства или поверхностью удара будем называть множество точек удовлетворяющих хотя бы одному уравнению

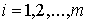, (8.3)

Мы будем предполагать, что удерживающие и односторонние связи являются непрерывными по , а односторонние связи являются гладкими по 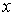– первого класса гладкости, так, что в каждой точке конфигурационного пространства можно определить пространство возможных перемещений.

Возможные перемещения удерживающих связей. Пространство возможных перемещений удерживающих связей в точке обозначается 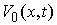. Оно определяются так же, как и в предыдущем разделе. Возможным перемещением удерживающих связей в точке называется любой вектор 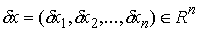удовлетворяющий условию

. (8.4)

Возможные перемещения. Пространство возможных перемещений в точке обозначается . Для точек, лежащих внутри области (8.1) оно определяется как пространство 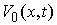возможных перемещений удерживающих связей. Для точек, лежащих на границе области (8.1), мы требуем также, чтобы вектор возможного перемещения 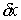касался этой границы, т.е. чтобы вдобавок к (8.4) выполнялось следующее условие:

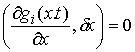для тех , для которых

здесь означает обычное скалярное произведение векторов 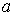и .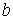

Конус допустимых направлений. Мы также будем предполагать, что в каждой точке поверхности удара можно определить конус 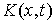допустимых направлений. Он представляет собой замыкание конуса возможных перемещений, сдвигаясь вдоль которых мы попадаем внутрь области, допустимой связями (8.1). Формально конус допустимых направлений, в добавление к условиям (8.4), определяется системой неравенств

для тех , для которых

Также мы будем считать, что односторонние связи являются непротиворечивыми, т.е. что конус допустимых направлений не пуст и содержит в себе пространство возможных перемещений. Для внутренних точек конфигурационного пространства конус 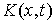допустимых направлений будем полагать совпадающим с пространством возможных перемещений .

Пример. Пусть, например, односторонняя связь задается одним неравенством 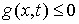. Тогда мы предполагаем, что – гладкая функция, и во всех точках 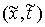, в которых равномерно выполнено . Пространство возможных перемещений в точке 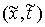является пересечением пространства 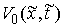с гиперплоскостью , задаваемой уравнением 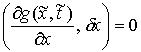. Конус допустимых направлений является пересечением пространства 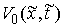с полупространством задаваемым неравенством .

Вернемся теперь к нашей системе. Мы будем рассматривать движение на некотором отрезке времени .

Вариацией кривой 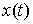будем называть непрерывную вектор-функцию .

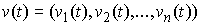Возможные вариации Вариацию 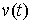кривой 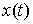будем называть возможной, если 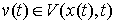для всех 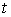, т.е. вектор 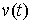является возможным перемещением в точке 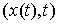. Отличие от определения возможной вариации для случая только удерживающих связей состоит в том, что во всех точках 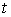, в которых кривая 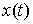выходит на границу односторонних связей, вектор 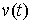касается границы односторонних связей.

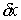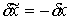Очевидно, что если перемещение является возможным в некоей точке , то и перемещение также является возможным в этой точке. Поэтому если вариация 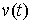является возможной, то и вариация 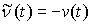также является возможной.

Допустимые вариации. Вариацию 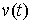кривой 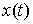будем называть допустимой, если 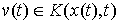для всех 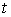, т.е. вектор 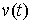является допустимым перемещением в точке 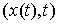. Отличие от определения возможной вариации состоит в том, что во всех точках 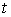, в которых кривая 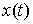выходит на границу односторонних связей, вектор 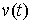лежит в конусе допустимых направлений . Поскольку конус допустимых перемещений содержит пространство возможных перемещений, то любая возможная вариация является допустимой.

Уравнения движения мы будем строить исходя из следующих принципов.

Принцип освобождения от связей. Пусть 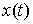– траектория движения системы со связями (7.3, 8.1). Тогда систему можно освободить от связей и добавить некую силу – реакцию связей 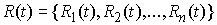таким образом, что кривая 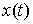останется траекторией освобожденной системы. При этом компоненты реакции связей представляют собой меры Лебега-Стилтьеса , имеющие особенности, сосредоточенные на множестве тех моментов времени, в которые траектория 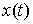выходит на односторонние ограничения.

Траектория системы представляет собой такую дифференцируемую функцию 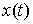, производная которой, 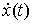является функцией с ограниченной вариацией. При этом будут справедливы следующие уравнения.

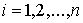, (8.5)

Идеальность связей (полная). Связи (7.3, 8.1) называются (вполне) идеальными, если для любой траектории системы 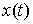, для любой ее допустимой вариации 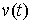интегральная элементарная работа сил реакции связей неотрицательна, т.е.

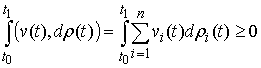(8.6)

Это условие означает, что при выходе действительной траектории системы на границу удерживающих связей реакция связей направлена внутрь области, допустимой этими связями.

Двусторонняя идеальность связей. Связи называются двусторонне идеальными, если для любой траектории движения системы 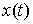для любой ее возможной вариации 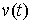интегральная элементарная работа сил реакции односторонних связей равна нулю, т.е.

(8.7)

Из полной идеальности связей вытекает их двусторонняя идеальность. В самом деле, допустим противное, что связи являются вполне, но не двусторонне идеальными. Тогда существует возможная (и, следовательно, допустимая) вариация 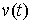такая, что 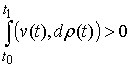. Взяв возможную (и, следовательно, допустимую) вариацию , получим 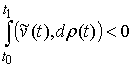, что противоречит (8.6). Доказательство закончено.

Найдя 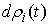из (8.5) и подставив в (8.6) получим эквивалентную форму записи условия полной идеальности связей. Для любой допустимой вариации 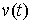должно выполняться

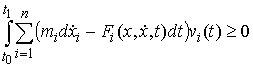(8.8)

Аналогично для условия двусторонней идеальности связей (8.7). Для любой возможной вариации 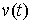должно выполняться

(8.9)

Принцип Даламбера-Лаграгжа. Пусть непрерывная кривая 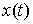удовлетворяет уравнениям связей (7.3, 8.1), а ее производная существует почти всюду и является функцией ограниченной вариации. Кривая 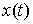является траекторией движения системы с идеальными связями (7.3, 8.1) тогда и только тогда, когда для любой допустимой вариации 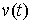выполнены соотношения (8.8) и, следовательно, для любой возможной вариации, соотношения (8.9).

Пользуясь леммой об аннуляторе (см. п. 4) мы получаем уравнения Лагранжа первого рода.

Уравнения Лагранжа первого рода. Принцип Даламбера-Лагранжа эквивалентен следующим уравнениям Лагранжа первого рода. Пусть непрерывная кривая 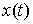удовлетворяет уравнениям связей (7.3, 8.1), а ее производная существует почти всюду и является функцией ограниченной вариации. 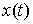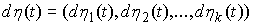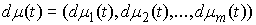Кривая является траекторией движения системы с (вполне) идеальными связями (7.3, 8.1) тогда и только тогда, когда найдутся такие векторные меры Лебега-Стилтьеса и , что

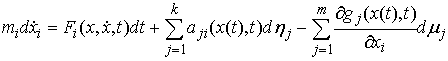(8.10)

При этом каждая мера 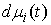неотрицательна и сосредоточена на множестве моментов времени, в которые 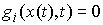. Для безударных движений, когда траектории являются гладкими (скорости непрерывны по времени), эти уравнения совпадают с обычными уравнениями Лагранжа первого рода.

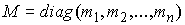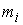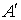Матричная форма уравнений. Пусть – диагональная матрица, с элементами на диагонали, – сводный вектор сил, – транспонированная матрица 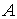из (7.3), 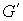– транспонированная матрица Якоби 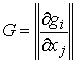. Тогда уравнения (8.10) можно записать в более компактной форме

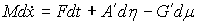(8.11)

Замечание о скачках. Любая функция ограниченной вариации есть сумма непрерывной функции и функции скачков представляющей собой ступенчатую функцию с не более чем счетным числом ступеней. В точках скачка функций и (и только в них) траекторная скорость также может иметь скачок. Обозначим эти скачки соответственно 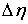, 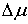и 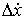. В силу (8.10), они связаны следующим соотношением

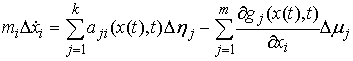(8.12)

или, более кратко

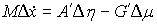(8.13)

Поскольку во все время движения выполнены уравнения удерживающих связей (7.3), то 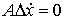и из (8.13) получаем

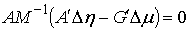(8.14)

Таким образом, скачк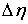и и 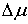не являются независимыми. Они связаны системой 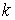линейных соотношений.

Дата добавления: 2015-05-23