
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Материал из Википедии — свободной энциклопедии
|
|
|
|
Теорема разложения Гельмгольца
Три теоремы Гельмгольца о вихрях.
[править]
Перейти к: навигация, поиск
Теорема разложения Гельмгольца — утверждение о разложении произвольного дифференцируемого векторного поля на две компоненты:
Если дивергенция и ротор векторного поля  определен в каждой точке конечной открытой области V пространства, то всюду в V функция может быть представлена в виде суммы безвихревого поля определен в каждой точке конечной открытой области V пространства, то всюду в V функция может быть представлена в виде суммы безвихревого поля  и соленоидального поля и соленоидального поля 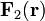 : :
 где
где
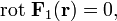
 для всех точек
для всех точек 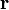 области V. области V.
|
Содержание
[убрать]
|
// [править] Формулировка теоремы
Пусть F — векторное поле в R ³, и пусть оно дважды непрерывно дифференцируемо и убывает быстрее чем 1/ r на бесконечности.[1] Тогда F представимо в виде суммы градиента и ротора как написано ниже:

Где  это оператор ньютониан (Если он действует на векторное поле вроде ∇ × F, он действует на каждую его компоненту).
это оператор ньютониан (Если он действует на векторное поле вроде ∇ × F, он действует на каждую его компоненту).
Если F имеет нулевую дивергенцию, ∇· F = 0, то F называется соленоидальным или бездивергентным, и разложение Гельмгольца поля F сокращается до

В этом случае, A называется векторным потенциалом поля F. Этот частный случай бездивергентного векторного потенциала в физике называется условием кулоновской калибровки (или нормировки).
В случае, если F имеет нулевой ротор, ∇× F = 0, то F называется безвихревым или локально потенциальным полем, а разложение F принимает вид

В этом случае, φ называется скалярным потенциалом поля F.
В общем случае F представимо суммой,
 ,
,
где отрицательный градиент скалярного потенциала — безвихревая компонента поля, а ротор векторного потенциала — соленоидальная.
|
|
|
[править] Поля, определенные ротором и дивергенцией
Теорема Гельмгольца работает также в следующих условиях. Пусть C — соленоидальное векторное поле, а d — скалярное поле в R ³, которые достаточно гладки и убывают быстрее 1/ r ² на бесконечности. Тогда существует векторное поле F такое, что
 и
и 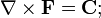
Если к тому же, если векторное поле F исчезает при r → ∞, тогда F единственно.[1]
Другими словами, при определенных условиях векторное поле может быть построено по его ротору и дивергенции, если же оно исчезает на бесконечности, то оно может быть построено однозначно. Эта теорема имеет огромное значение в электростатике, например уравнения Максвелла в статическом случае описывают поля как раз этого типа.[1] Как уже было написано выше:
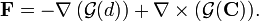
 . Скоростное поле сплошной среды в окрестности точки. Первая теорема Гельмгольца
. Скоростное поле сплошной среды в окрестности точки. Первая теорема Гельмгольца
В движущейся жидкости связь между скоростями точек имеет сложный вид. Это связано с возможностью перемещения отдельных частиц относительно им подобных, что приводит к деформации выделенного объема.
Скорость любой точки потока жидкости можно описать функцией, зависящей от координат
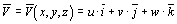 ,
,
где u=u(x,y,z), v=v(x,y,z) и w=w(x,y,z) - проекции вектора скорости на оси координат; 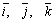 - орты декартовых осей координат.
- орты декартовых осей координат.
Любую непрерывную функцию в окрестности точки "0" можно разложить в ряд Тейлора, причем, если под понятием "окрестности" понимать область, в которой точки отстоят от "0" на очень малое расстояние 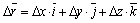 , то в разложении можно ограничиться только линейными членами ряда. Для проекции на ось x получим
, то в разложении можно ограничиться только линейными членами ряда. Для проекции на ось x получим
 upofloor паркетная доска
upofloor паркетная доска
Используя тождества
 ,
,
выражение для проекции скорости на ось x приведем к виду
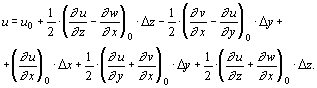 (1.3.1)
(1.3.1)
Аналогично можно получить формулы для проекций вектора скорости на оси координат y и z.
Вращательное движение тела характеризуется вектором угловой скорости. Представим вектор угловой скорости вращения через его проекции на оси координат
|
|
|
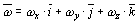 .
.
В разделе математики "Векторная алгебра" показано, что

С учетом этого, второе и третье слагаемые в правой части уравнения (1.3.1) представляют собой проекцию на ось x следующего векторного произведения
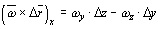 ,
,
которое в сумме с u 0 представляет собой выражение, тождественно равное проекции скорости движения абсолютно твердого тела на рассматриваемую ось
 .
.
Величину 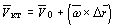 называют скоростью квазитвердого движения жидкой частицы. Последние три слагаемые уравнения (1.3.1)
называют скоростью квазитвердого движения жидкой частицы. Последние три слагаемые уравнения (1.3.1)
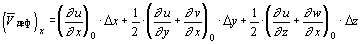
являются проекцией на ось x вектора деформационного движения  .
.
На основании вышеизложенного можно сформулировать следующее утверждение, известное как первая теорема Гельмгольца: скорость точек элементарного объема жидкости складывается из скоростей квазитвердого и деформационного движений. Векторная запись этой теоремы имеет вид
 . (1.3.2)
. (1.3.2)
|
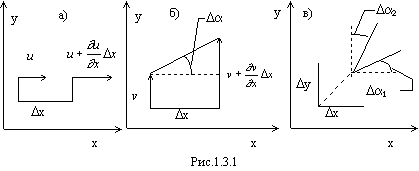
Для выяснения смысла вектора деформационного движения рассмотрим некоторые частные случаи.
На рис. 1.3.1, а представлено движение отрезка Dx вдоль оси x. Пусть левый конец отрезка движется со скоростью u, а правый - со скоростью 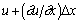 . Из-за разности скоростей длина отрезка за время D t изменится на
. Из-за разности скоростей длина отрезка за время D t изменится на 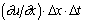 , а скорость изменения длины (скорость линейной деформации) будет
, а скорость изменения длины (скорость линейной деформации) будет 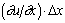 . Отношение скорости линейной деформации к первоначальной длине отрезка называют относительной (удельной) скоростью линейной деформации exx. Аналогично можно получить относительные скорости линейной деформации вдоль других координатных осей.
. Отношение скорости линейной деформации к первоначальной длине отрезка называют относительной (удельной) скоростью линейной деформации exx. Аналогично можно получить относительные скорости линейной деформации вдоль других координатных осей.
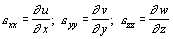 .
.
Из рассмотрения движения отрезка Dx вдоль оси y (рис. 1.3.1, б) следует, что если скорость его левого конца v, а правого  , то за время D t отрезок переместится и повернется на угол Da1. Для малых углов
, то за время D t отрезок переместится и повернется на угол Da1. Для малых углов
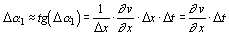 .
.
Угловая скорость такого поворота равна
 .
.
Угловая скорость поворота отрезка Dy (рис. 1.3.1, в) равна 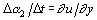 .
.
Вследствие вращения отрезков Dx и Dy, расположенных первоначально под прямым углом, произойдет угловая деформация частицы в плоскости x-y. Скорость угловой деформации определяется суммой угловых скоростей поворота обоих отрезков т.е.  . В гидравлике за меру скорости угловой деформации принимают половину этой суммы, т.е.
. В гидравлике за меру скорости угловой деформации принимают половину этой суммы, т.е.
 .
.
Аналогично получают меры скоростей угловых деформаций в плоскостях y-z и x-z
|
|
|
 .
.
На основании вышеизложенного, проекции вектора деформации на оси координат можно представить в следующем виде:
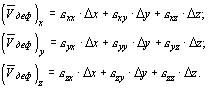 (1.3.3)
(1.3.3)
Скорости линейных и угловых деформаций образуют тензор скоростей деформации 
 (1.3.4)
(1.3.4)
Выражение для скорости деформационного движения, с учетом этих обозначений, примет вид:
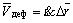 .
.
|
|
|
|
|
Дата добавления: 2015-05-23; Просмотров: 1024; Нарушение авторских прав?; Мы поможем в написании вашей работы!