
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод мінімальної вартості
|
|
|
|
Відмінність від попереднього методу полягає в тому, що на кожному кроці для включення в план вибирають найдешевший (тобто з мінімальним нормативом транспортних витрат) маршрут серед можливих, замість самого північно-західного. Обсяг вантажу, що перевозиться за визначеним маршрутом, і правило виключення з розгляду постачальників або споживачів зберігаються.
Приклад 5. Методом мінімальної вартості знайти опорний план ТЗ, умова якої задається таблицею (попередній приклад):
| Постачальники | Споживачі | Запаси | |||||||
| Потреби |
Опорний план:
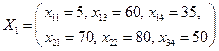

Порівнюючи план перевезень, визначений методом північно-західного кута, з планом перевезень, знайденим методом мінімальної вартості, бачимо, що перевезення тієї самої кількості вантажів здійснено при менших транспортних витратах (765 проти 1295).
Зауваження. Варто зазначити, що ознакою опорності плану ТЗ є його ациклічність, тобто неможливість побудови циклу. Циклом транспортної задачі називають замкнену ламану лінію, вершини якої розміщуються в заповнених клітинках таблиці, а сторони проходять уздовж рядків і стовпчиків таблиці.
Якщо опорний план є виродженим, то для подальшого розв'язання задачі необхідно заповнити відповідну кількість порожніх клітинок, записуючи в них "нульове перевезення", але так, щоб при цьому не порушилася ациклічність плану.
3. На даному етапі розв’язування ТЗ визначають потенціали опорного розв’язку, який був отриманий одним із вищерозглянутих методів. Поняття потенціалу пов’язане із двоїстою до транспортної задачею. Випишемо цю пару взаємодвоїстих задач:
|
|
|
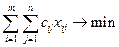 , (13) , (13) 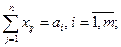 (14) (14) 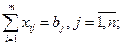 (15) (15) 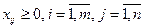 . (16) . (16)
| 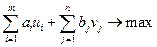 (17) (17)
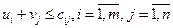 . (18) . (18)
|
У двоїстій задачі (17)–(18) 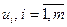 – двоїсті змінні, які відповідають обмеженням (14) і називаються потенціалами постачальників,
– двоїсті змінні, які відповідають обмеженням (14) і називаються потенціалами постачальників, 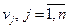 – двоїсті змінні, які відповідають обмеженням (15) і називаються потенціалами споживачів.
– двоїсті змінні, які відповідають обмеженням (15) і називаються потенціалами споживачів.
Визначають потенціали опорного плану розв’язавши систему рівнянь 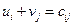 , яка формується для всіх заповнених клітинок транспортної таблиці.
, яка формується для всіх заповнених клітинок транспортної таблиці.
Оскільки для невиродженого початкового опорного плану заповнених клітинок є 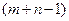 , то для визначення чисел
, то для визначення чисел 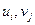 необхідно розв’язати систему з
необхідно розв’язати систему з 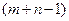 рівнянь з
рівнянь з 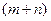 змінними. Така система є невизначеною. Для усунення невизначеності одній із змінних надається довільне значення, наприклад покладають
змінними. Така система є невизначеною. Для усунення невизначеності одній із змінних надається довільне значення, наприклад покладають 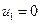 . Тоді розв’язок системи визначається однозначно.
. Тоді розв’язок системи визначається однозначно.
4. При перевірці опорного плану ТЗ на оптимальність за допомогою потенціалів користуються наступним твердженням.
Теорема. (умова оптимальності опорного плану ТЗ).
Якщо для деякого опорного плану 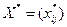 існують потенціали
існують потенціали 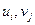 , для яких виконуються умови:
, для яких виконуються умови:
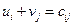 для всіх значень
для всіх значень 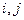 , для яких
, для яких 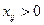 , (19)
, (19)
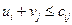 для всіх значень
для всіх значень 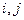 , для яких
, для яких 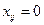 , (20)
, (20)
то він є оптимальним планом транспортної задачі. Якщо хоча б для однієї клітинки ця умова не виконується, тобто 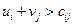 , то поточний план є неоптимальним і від нього необхідно перейти до нового опорного плану.
, то поточний план є неоптимальним і від нього необхідно перейти до нового опорного плану.
Перехід від одного опорного плану до іншого виконується заповненням клітинки, для якої порушено умову оптимальності. Якщо таких клітинок кілька, то для заповнення вибирають таку, що має найбільше порушення, тобто таку, для якої 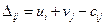 є найбільшим.
є найбільшим.
Для вибраної порожньої клітинки будують цикл перерахування та виконують перерозподіл продукції в межах цього циклу за такими правилами:
1) кожній вершині циклу приписують певний знак, причому вільній клітинці – знак «+», а всім іншим по черзі – знаки «–» та«+»;
|
|
|
2) у порожню клітинку переносять менше з чисел 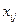 , що стоять у клітинках зі знаком «–», яке позначають через
, що стоять у клітинках зі знаком «–», яке позначають через  . Одночасно це число додають до відповідних чисел, які розміщуються в клітинках зі знаком «+».
. Одночасно це число додають до відповідних чисел, які розміщуються в клітинках зі знаком «+».
Отже, клітинка, що була вільною, стає заповненою, а відповідна клітинка з мінімальним числом 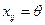 стане порожньою. У результаті такого перерозподілу продукції отримується новий опорний план транспортної задачі.
стане порожньою. У результаті такого перерозподілу продукції отримується новий опорний план транспортної задачі.
5. Далі повторюються кроки алгоритму, починаючи з кроку 3.
Розглянемо застосування методу потенціалів на прикладі.
Приклад 6. Розв'язати методом потенціалів транспортну задачу, умова якої задається наступною таблицею:
| Постачальники | Споживачі | Запаси | |||||||
| Потреби |
Знайдемо перший опрний розв’язок методом мінімальної вартості:
| Постачальники | Споживачі | Запаси | 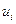
| |||||||||||
| – | + | |||||||||||||
| + | – | |||||||||||||
| Потреби | ||||||||||||||
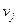
| –2 | |||||||||||||
| (1,2) | -2+0<=5 | + | ||||||||||||
| (1,3) | 0+0<=6 | + | ||||||||||||
| (2,1) | 1+3<=4 | + | ||||||||||||
| (2,4) | 1+3<=4 | + | ||||||||||||
| (3,1) | 1+5<=3 | – | 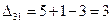
| |||||||||||
| (3,2) | -2+5<=3 | + | ||||||||||||
Будуємо цикл перерахування клітини (3,1) (вершини циклу позначені на рисунку). Нумеруємо вершини плюсами та мінусами, визначаємо 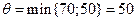 . До клітинок з "+" додаємо 50, від клітин з "–" віднімаємо 50. Отримуємо новий опорний розв'язок, який аналогічно перевіряємо на оптимальність за допомогою потенціалів.
. До клітинок з "+" додаємо 50, від клітин з "–" віднімаємо 50. Отримуємо новий опорний розв'язок, який аналогічно перевіряємо на оптимальність за допомогою потенціалів.
| Постачальники | Споживачі | Запаси | 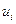
| ||||||||||
| Потреби | |||||||||||||
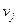
| |||||||||||||
| (1,2) | 0+1<=5 | + | |||||||||||
| (1,3) | 0+3<=6 | + | |||||||||||
| (2,1) | 0+1<=4 | + | |||||||||||
| (2,4) | 0+1<=4 | + | |||||||||||
| (3,2) | 2+1<=3 | + | |||||||||||
| (3,4) | 2+1<=6 | + | |||||||||||
Умова оптимальності виконується.
|
|
|
Розв’язок транспортної задачі має вигляд:
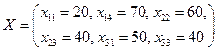
 .
.
Ігрові моделі в управлінні економічним ризиком
Управління економічним ризиком — це система заходів, спрямованих на уникнення ризику, зменшення його показників, а також на вироблення стратегії діяльності та прийняття рішень в умовах ризикованої ситуації.
Теорія ігор – це розділ сучасної математики, який вивчає математичні моделі прийняття рішень в умовах невизначеності, конфліктності, тобто в ситуаціях, коли інтереси сторін або протилежні, або не збігаються.
Засновниками теорії ігор вважають американців Дж. фон Неймана (1903-1957) і О. Моргенштерна (1902-1977), які в 40-х роках 20-го століття описали явище конкуренції як деяку "гру".
Гра – це формалізований опис (модель) конфліктної ситуації, яка включає в себе чітко визначені правила дій її учасників, котрі намагаються отримати певну перемогу шляхом вибору конкретної (в певному сенсі – найкращої) стратегії поведінки. При цьому суб'єкт керування (суб'єкт прийняття рішення – СПР) називається гравцем. У грі може брати участь два гравці (парна гра) чи кілька гравців (множинна гра).
В теорії ігор розглядаються ситуації, які пов’язані з прийняттям рішень, в яких два супротивники переслідують цілі, які конфліктують між собою. Типовими прикладами таких ситуацій є реклама товарів, які конкурують на ринку, планування стратегій двох армій, які беруть участь у воєнному конфлікті. Ці ситуації прийняття рішень відрізняються від попередніх, де природа не розглядалась як супротивник.
|
|
|
У ігровому конфлікті беруть участь два гравці, кожний володіє певним набором (скінченним або нескінченним) можливих виборів, які називаються стратегіями. З кожною парою стратегій пов'язаний платіж, який один із гравців виплачує іншому. Такі ігри називаються іграми двох осіб з нульовою сумою, оскільки виграш одного з гравців дорівнює програшу іншого. У такій грі достатньо задати результати у вигляді платежів для одного з гравців.
Позначимо гравців через А та В. Гравець А обирає одну з 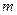 стратегій
стратегій 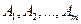 ; гравець В – одну з
; гравець В – одну з 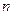 стратегій
стратегій  . Якщо гравець А використає стратегію
. Якщо гравець А використає стратегію 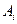 , а гравець В –
, а гравець В – 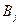 , то платіж гравцеві А складатиме
, то платіж гравцеві А складатиме 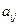 , а відповідно гравцеві В – (
, а відповідно гравцеві В – (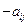 ).
).
Матриця, складена із величин 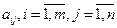 називається платіжною матрицею гравця А, або матрицею гри:
називається платіжною матрицею гравця А, або матрицею гри:
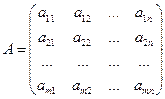 .
.
Завдання кожного з гравців – знайти найкращу стратегію гри, при цьому вважається що кожен з гравців діє у власних інтересах. Якщо гравець А обрав стратегію 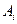 , то у найгіршому випадку він отримає виграш
, то у найгіршому випадку він отримає виграш 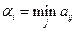 . Передбачивши таку можливість, гравець повинен обрати таку стратегію, щоб максимізувати свій гарантований (мінімальний) виграш.
. Передбачивши таку можливість, гравець повинен обрати таку стратегію, щоб максимізувати свій гарантований (мінімальний) виграш.
Величина 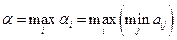 , яка є гарантованим виграшем гравця А, називається нижньою ціною гри. Стратегія, яка забезпечує отримання виграшу величиною
, яка є гарантованим виграшем гравця А, називається нижньою ціною гри. Стратегія, яка забезпечує отримання виграшу величиною 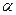 називається максмінною.
називається максмінною.
Якщо гравець А буде притримуватись своєї максмінної стратегії, то у нього є гарантія того, що у любому випадку він виграє не менше ніж 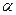 .
.
Аналогічно визначається найкраща стратегія гравця В. Гравець 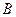 при виборі стратегії
при виборі стратегії 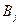 в найгіршому варіанті отримає програш
в найгіршому варіанті отримає програш 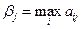 . Він обиратиме стратегію, при якій програш буде мінімальним.
. Він обиратиме стратегію, при якій програш буде мінімальним.
Величина 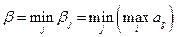 , яка є гарантованим програшем гравця В, називається верхньою ціною гри. Стратегія, яка забезпечує отримання програшу величиною
, яка є гарантованим програшем гравця В, називається верхньою ціною гри. Стратегія, яка забезпечує отримання програшу величиною 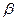 називається мінімаксною.
називається мінімаксною.
Якщо гравець B буде притримуватись своєї мінімаксної стратегії, то у нього є гарантія того, що у любому випадку він програє не більше ніж 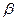 .
.
Фактичний виграш гравця А (програш гравця В) при свідомих діях супротивників обмежений верхньою та нижньою цінами гри. Для матричної справедливо, що 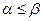 .
.
Якщо  , тобто
, тобто 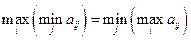 , то спільне значення нижньої та верхньої ціни гри називається ціною гри і позначається
, то спільне значення нижньої та верхньої ціни гри називається ціною гри і позначається 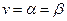 . В такому випадку кажуть, що гра має сідлову точку, яка відповідає набору оптимальних стратегій обох гравців. Якщо гра має сідлову точку, то кажуть, що для неї існує розв’язок у чистих стратегіях.
. В такому випадку кажуть, що гра має сідлову точку, яка відповідає набору оптимальних стратегій обох гравців. Якщо гра має сідлову точку, то кажуть, що для неї існує розв’язок у чистих стратегіях.
Приклад 7. Дослідити ігри на наявність сідловок точки
а) 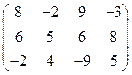 ; б)
; б)  .
.
Розв’язання: а) Обчислимо нижню та верхню ціну гри:
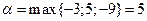 ;
;
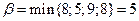 .
.
Оскільки для даної гри 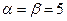 , то для неї існує розв’язок у чистих стратегіях, якому відповідає сідлова точка. Ціна гри для обох гравців
, то для неї існує розв’язок у чистих стратегіях, якому відповідає сідлова точка. Ціна гри для обох гравців 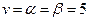 .
.
б) Обчислимо нижню та верхню ціну гри:
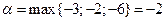 ;
;
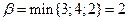 .
.
Оскільки для даної гри 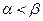 , то для неї не існує розв’язку в чистих стратегіях.
, то для неї не існує розв’язку в чистих стратегіях.
Якщо платіжна матриця не має сідловок точки, тобто 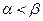 , то пошук розв’язку призводить до застосування складної стратегії, яка полягає у змішуванні двох або більше стратегій з певними ймовірностями (частотами). Такий розв’язок гри називається розв’язком у змішаних стратегіях.
, то пошук розв’язку призводить до застосування складної стратегії, яка полягає у змішуванні двох або більше стратегій з певними ймовірностями (частотами). Такий розв’язок гри називається розв’язком у змішаних стратегіях.
Якщо матриця гри має розмірність 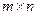 , то стратегії гравця А задаються наборами ймовірностей
, то стратегії гравця А задаються наборами ймовірностей 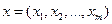 , з якими гравець застосовує свої чисті стратегії
, з якими гравець застосовує свої чисті стратегії 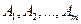 . Дані ймовірності задовольняють умови:
. Дані ймовірності задовольняють умови: 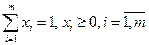 .
.
Аналогічно, для гравця В маємо набори ймовірностей 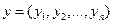 , з якими гравець застосовує свої чисті стратегії
, з якими гравець застосовує свої чисті стратегії  . Дані ймовірності задовольняють умови:
. Дані ймовірності задовольняють умови: 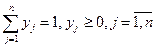 .
.
У такому випадку (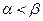 ) розв’язати гру фактично означає знайти невідомі набори ймовірностей
) розв’язати гру фактично означає знайти невідомі набори ймовірностей 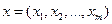 та
та 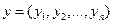 з якими гравці змішуватимуть свої стратегії.
з якими гравці змішуватимуть свої стратегії.
Приклад 8. Розв’язати гру, яка задається матрицею:
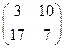 .
.
Розв’язання: Знайдемо нижню та верхню ціну гри:
 ;
; 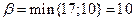 .
.
Знаходження розв'язку у змішаних стратегіях зводиться до знаходження ймовірностей 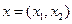 та
та 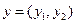 . Якщо гравець В застосує стратегію
. Якщо гравець В застосує стратегію 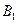 (або
(або 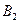 ), то гравець А отримає виграш, що дорівнює ціні гри, врахувавши також зміст
), то гравець А отримає виграш, що дорівнює ціні гри, врахувавши також зміст 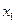 та
та 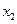 , отримаємо наступну систему рівнянь:
, отримаємо наступну систему рівнянь:
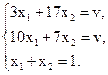
Віднявши від першого рівняння друге, отримаємо систему двох рівнянь з двома невідомими, яка має розв’язок:
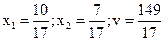 .
.
Для іншого гравця отримаємо наступну систему:
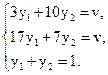
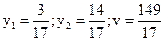 .
.
Отже, розв'язок гри для гравця А полягає у змішуванні стратегій 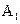 та
та 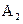 з ймовірностями
з ймовірностями 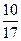 та
та 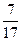 відповідно, для гравця В - у змішуванні стратегій
відповідно, для гравця В - у змішуванні стратегій 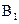 та
та 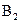 з ймовірностями
з ймовірностями 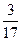 та
та 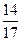 відповідно. Ціна гри для обох гравців
відповідно. Ціна гри для обох гравців 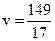 .
.
ВАРІАНТИ КОНТРОЛЬНОЇ РОБОТИ
|
|
|
|
|
Дата добавления: 2015-05-23; Просмотров: 952; Нарушение авторских прав?; Мы поможем в написании вашей работы!