Нормальний розподіл

Важливу роль у теорії ймовірностей відіграє нормальний закон розподілу. Назва “нормальний” пояснюється тим, що через поширеність цього закону при описі більшості природніх явищ, він сприймався як норма (стандарт) розподілу будь-якої випадкової величини. Цьому закону підпорядковані більшість числових характеристик властивостей особистості і людських здібностей.

Випадкова величина має номальний розподіл (або розподіл Гауса), якщо щільність її розподілу задається рівністю

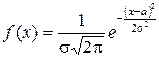. (ІІ.23)

Функція нормального розподілу має вигляд

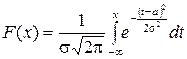. (ІІ.24)

Числові характеристики нормально розподіленої випадкової величини дорівнюють

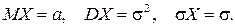(ІІ.25)

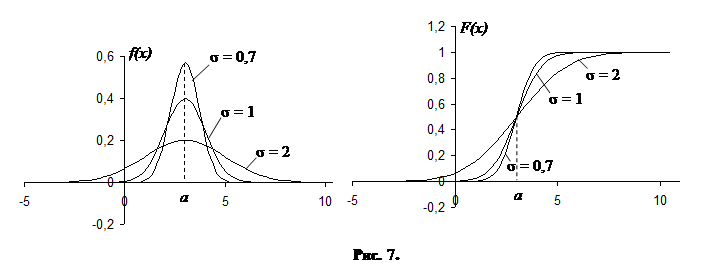
Залежно від параметра 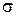графіки щільності розподілу та функції розподілу мають такий вигляд

Нормальний розподіл з параметрами 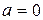та 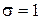називають стандартним нормальним розподілом. Для стандартного нормального розподілу складені таблиці його щільності та функції Лапласа (Див. таблиці 1 і 2 в додатку 1).

В пакеті Excel для обчислення щільності та функції нормального розподілу служать статистичні функції НОРМРАСП і НОРМСТРАСП. Квантилі нормального розподілу можна обчислити, користуючись функціями НОРМОБР та НОРМСТОБР.

Імовірність попадання нормально розподіленої випадкової величини в заданий інтервал визначається за формулою

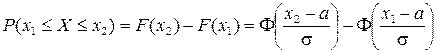(ІІ.26)

При використанні формули (ІІ.26) слід пам’ятати, що функція Лапласа Ф(х) є непарною функцією, тобто Ф(– х) = – Ф(х).

Імовірність відхилення нормально розподіленої випадкової величини від свого математичного сподівання не більше, ніж на ε, обчислюється за формулою

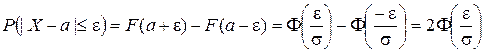(ІІ.27)

Зокрема, послідовно вибираючи 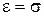, , 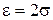, 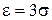отримуємо:

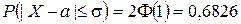
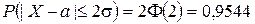
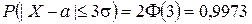(ІІ.28)

Останнє співідношення виражає правило “трьох сігм”, яке полягає в тому, що практично всі значення нормально розподіленої випадкової величини відхиляються від свого математичного сподівання не більше, ніж на .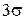

Приклад 11. Випадкова величина розподілена за нормальним законом з математичним сподіванням а = 10. Знайти ймовірність попадання випадкової величини в інтервал (20; 30), якщо ймовірність її попадання в інтервал (0; 10) дорівнює 0,3.

Розв’язання: Оскільки ймовірність попадання нормально розподіленої випадкової величини у заданий інтервал визначається за формулою (ІІ.26), то 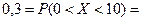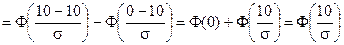. З таблиці значень функції Лапласа визначаємо 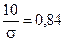, звідки 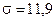. Далі .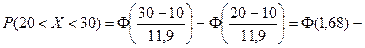

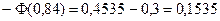Дата добавления: 2015-05-23