
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Апромаксимація. Метод найменших квадратів
|
|
|
|
Інтерполяційний багаточлен Лангранжа
Ln(x) = 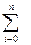 yiLi(n)(x) – в обчислення вводяться зразу всі точки
yiLi(n)(x) – в обчислення вводяться зразу всі точки
Li(n)(x) = 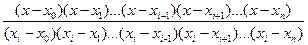
Коефіцієнти Лангранжа які задовільняють умовам:
Li(n)(xі) =1, Li(n)(xj) = 0 при i≠j
Блок-схема алгоритму
Це є глобальна інтерполяція, тобто випадок коли експериментальне значення замінюються деякою функцією, яка описує їх у всіх точках x0, x1, x2…,xn. Тобто інтегральна функція повинна проходити через всі експериментальні точки. Їх вигляд
L(x) = y0l0(x)+ y1l1(x) +…+ ynln(x)
Тобто вона є лінійною комбінацією многочленів степені n. Многочлени li(x)вибираються із таких умов.
l0(x)=1 в точках х=х0 і l0(x)=0 у всіх інших точках
l1(x)=1 в точках х=х1 і=0 у всіх інших точках
ln(x)=1 в точках х=хn i=0 у всіх інших точках
l0(х)= 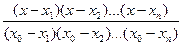
l1(x)= 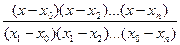
.
.
.
li(x)= 
Із збільшенням n труднощі побудови інтерполяційного багаточлену зростають суттєво. Але необхідність в точному відтворенні функції виникає не завжди і часто достатньо мати багаточлен значно меншого степені наприклад, лінійну функцію або квадратний тричлен, що відтворюють основні закономірності досліджуваної залежності.
Тому, природньо поставити задачу про визначення баготочлену більш низького степені m<n
Pm(x)=amxm+am-1xm-1+...+a0 (1)
“віддаль” між ним і функціє F(x), в деякому змісті, мінімальна. Такий багаточлен називається апроксимуючим. Він згладжує локальні особливості заданої експериментальної таблиці і відображає загальну поведінку функції f(x) вздовж всього інтервалу зміни. Розглянем метод найменших квадратів, що розв’язує цю задачу.
Нехай задана таблиця значень функції y=f(x) {xі,yі} i=1,n
Апроксимуюча функція шукається у вигляді
Y=j(x,a1,…am), де a1,…am параметри, що потрібно визначити.
Обчислимо (2) при х=xi
Y1=j(x,a1,…am), і=1,n.
|
|
|
Між досліджуваною і апроксимуючою функціями є відмінність, яку оцінимо за допомогою суми квадратів різниць їх значень:
S=S(a1,…am)=  (3)
(3)
параметри a1,…am знайдемо із умов min похибки апроксимації S
 (4)
(4)
отримуємо суму m-рівнянь для визначення m- невідомих параметрів.1
Апроксимація багаточленом.
Нехай апроксимуюча функція (2) має вигляд
Y=a1x+a0
Тоді (3)Þ  , а рівняння (4) будуть такими
, а рівняння (4) будуть такими

або  (5)
(5)
Звідки коефіцієнти а0 і а1 визначаються однозначно. Якщо апроксимуюча функція має вигляд (1), то коефіцієнти а0,...аm визначаються із системи лінійних рівнянь
 R0a0 + R1a1 +…+ Rmam = B0
R0a0 + R1a1 +…+ Rmam = B0
R1a0 + R2a1 +…+ Rm+1am = B1 (6)
.
.
.
Rma0 + R m+1a1 +…+ R 2mam = Bm, де
Rk =  , де k=0,2m (7)
, де k=0,2m (7)
Bj =  , j = 0,m
, j = 0,m
Приклад, задана таблиця значень max i min ємності шести “підстроювальних конденсаторів”. Потрібно апроксимувати ці дані лінійною залежністю.
| і | уі | уі | хі2 | хіуі |
| 4.4 4.4 4.7 4.7 4.5 4.6 | 2.3 2.1 2.3 2.5 2.2 2.4 | 19.36 19.36 22.09 22.09 20.25 21.16 | 10.12 9.24 10.84 11.75 9.90 11.04 | |
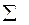
| 27.3 | 13.8 | 124.31 | 62.89 |
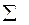 /n /n
| 4.55 | 2.3 | 20.72 | 10.48 |
R0a0+R1a1 = B0
 R1a0+R2a1 = B1
R1a0+R2a1 = B1
Згідно (5)
Þ  (2) 20.72а1 + 4.55а0 = 10.48
(2) 20.72а1 + 4.55а0 = 10.48
(1) 4.55а1 + 1а0 = 2.30
а1 = -0.86
а2 = 1.60
Апроксимуючою функцією буде у=0.86х – 1.60
В статистиці цю залежність називають рівнянням регресії у по х.
Похибка середньоквадратичної апроксимації функції визначається виразом:
D = [  ]1/2
]1/2
Алгоритм



Рекурсивні алгоритми.
Циклічні обчислювальні алгоритми в яких значення деякої функції (або функцій) на кожному наступному кроці обчислень залежить від значень цієї ж функції, отриманого на попередньому кроці обчислень, називають рекурсивними алгоритмами.
Обчислення функції при цьому проводяться за рекурсивними формулами. Прикладом є запис х=х+1; рекурсивними є алгоритмидля розв’язування таких задач як знаходження суми та добутку скінченного числа доданків; суми нескінченого ряду3; уточнених коренів лінійних рівнянь; знаходження max (min) значення із деякої множини значень. Рекурсивні алгоритми можуть бути скінченими та інтераційними.
|
|
|
Алгоритм обчислення суми ¥ ряду з заданою точністю ε:
S = 1+  =
= 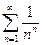
|a| - приріст суми.
Цей алгорим є ітераційним.

|
|
|
|
|
Дата добавления: 2015-05-23; Просмотров: 710; Нарушение авторских прав?; Мы поможем в написании вашей работы!