Метричний тензор у косокутних координатах 3 страница

-80-

Приклади корисніші від правил.

І.Ньютон.

23. Приклади тензорів.

У фізиці і в математиці дійсно існують величини, що мають більш складну розмірність ніж скаляр і вектори. Іншими словами, ми наведемо приклади тензорів.

У першу чергу нам треба показати, що попередньо введені величини /і відповідно – / є компонентами тензора.

Згадаємо, що

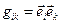
а при переході до нової системи

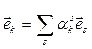
Тоді

- величини мають такі такі ж трансформаційні властивості як і коваріантні складові тензора другого рангу. Отже, є коваріантним симетричним тензором.

Аналогічно доводять, що є контрваріантним тензором.

Згадаємо тепер співвідношення /18.9/

І відзначимо, що операція 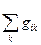є операцією опускання верхнього індексу. Тому

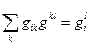
Де 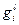є мішаними компонентами метричного цензора і

/23.1/

Згідно з загальним законом перетворення мішаних компонент тензора другого рангу ми маємо

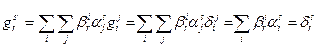
Отже,

- символ Кронекера є мішаним тензором другого рангу а його компоненти мають однакові

-ф-

значення

-81-

в усіх координатних системах.

Далі два приклади тензорів ми проведемо, обмежуючись декартовими координатними системами.

Приклад 1. Тензор інерції твердого тіла.

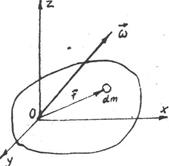
Розглянемо рух твердого тіла, що обертається з кутовою швидкістю 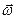навколо нерухомої точки 0. Приймемо точку 0 за початок координат і підрахуємо момент кількості руху тіла відносно точки 0.

Розглянемо елемент об’єму ,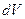

що рухається з лінійною швидкістю ,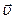

тоді

а момент кількості руху цього елемента

буде

рис.65 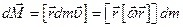/23.2/

Момент кількості руху всього тіла

Знайдемо підсумовуючи /23.2/ по всьому об’єму тіла.

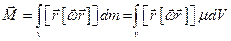
де 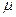густина речовини. Використавши формулу

ми одержимо

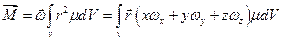
Проекції вектора –ф- на координатні осі дорівнюють

- -

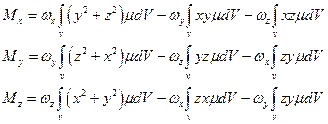Введемо позначення

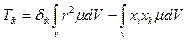
тоді

-84-

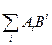є скалярним добутком векторів інваріантом, тобто тензором рангу нуль. Таким чином прирівнюючи два індекси /верхній і нижній/ у виразі і підсумовуючи по цьому індексу, ми понизимо ранг тензора на дві одиниці. Таку операцію називають згорткою.

Операцію згортання двох індексі можна здійснити для довільного тензора рангу N, понижуючи при цьому його ранг на дві одиниці.

Нехай даний тензор з N₁ коваріантними і N₂ контрваріантними індексами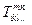

Запишемо його закон перетворення при переході до нової системи

І розглянемо суму

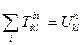
- вираз, що має N₁-1 коваріантних і N₂-1 контрваріантних рухомих індексів. Тоді

Враховуючи, що вираз у дужці є символом Кронекера 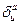одержуємо

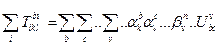
Тобто

Ми одержали закон перетворення тензора рангу

Підкреслюємо, що операція згортання за двома контрваріантними індексами не приводить до тензора нижчого рангу. Легко переконатись, що вирази

Не мають тензорної розмірності.

Цілком зрозуміло, що згортання по різних парах індексів, взагалі кажучи, дає рівні рель тати. Наприклад,

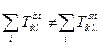
-85-

/знак рівності можна поставити тільки у випадку, коли тензор симетричний стосовно до пари індексів і -/.

Тензори четвертого і вищих рангів можна згортати по двох парах індексів

/24.2/

У результаті одержується тензор, ранг якого на чотири одиниці нижчий. В цьому легко переконатися, вивчаючи трансформаційні властивості виразу /24.2/.

Цікаво відзначити, що подвіцна згортка добутку симетричного і антисиметричного тензорів дорівнює нулеві. Нехай 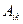симетричний, 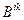- антисиметричний тензор другого рангу:

Тоді

Повернемось ще до згортки тензора другого рангу

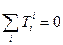
Цей вираз є інваріантом – сумою діагональних елементів матриці тензора 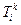. Його називають слідом матриці Т.

Коли задачу розв’язує інший, все ясно,

коли розв’язуєш сам, нічого не виходить.

Л.Ейлер

25. Деякі властивості симетричних тензорів другого рангу.

Будь-який тензор другого рангу можна записати на як суму двох тензорів – симетричного і антисиметричного. Тому доцільно вивчити окремо властивості симетричних і окремо властивості антисиметричних тензорів. Для простоти обмежимись розглядом цих тензорів у прямокутних системах координат.

Нехай Т_ік симетричний

Т_{ік =} Т_кі

І будемо розглядати випадок, коли його складові Т_іі дотатні.

Виберемо координатну систему xyz і розглянемо вираз

-86-

Він є згорткою двох тензорів: Т_ік і мішаного добутку Тому /25.1/ є інваріантом.

Розглянемо рівняння

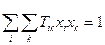/25.2/

у розгорнутому вигляді воно має вигляд

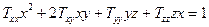
/25.2/

і є рівнянням поверхні другого порядку в системі xyz.

Щоб з’ясувати, з якою поверхнею ми маємо справу, знайдемо точки перетину цієї поверхні з координатними осями. Приймаючи y=z=0 знайдемо точки перетину поверхні з віссю х

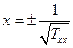
- з віссю х поверхня перетинається в двох скінченних симетрично розміщених точках. Аналогічно, приймаючи х=z=0. а також х=у=0

Знайдемо

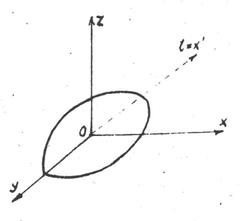
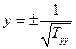
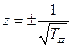
- з осями у і z поверхня перетинається в двох скінченних, симетрично розміщених точках.Щоб остаточно з’ясувати з якоюповерхнею ми маємо справу, знайдемо точки перетину поверхні /25.2/ з довільною прямою -, яка проходить через початок координат. Приймемо за вісь нової системи координат і врахуємо, що

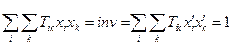
Якщо , тоді

точками перетину є знову дві скінченні, симетрично розміщені точки.

Поверхня /25.2/ з еліпсоїдом, однак, у загальному випадку його осі не збігаються з координатними осями х, у, z.

Виберемо ще одну координатну систему х, у, z, осі якої збіга-

-87-

ються з напрямками осей еліпсоїда. У цій системі

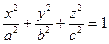де 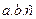, - довжина півосей еліпсоїда.

З другого боку

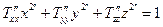але також

Останні дві рівності збігаються тільки тоді, коли

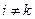
Таким чином, системі х, у, z матриця симетричного тензора набуває вигляду

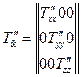
- недіагональні складові тензора перетворюються в нуль. Приходимо до висновку, що для будь якого симетричного тензора можна знайти таку систему координат, в якій відмінними від нуля є тільки три складові тензора.

Еліпсоїд, визначений за рівнянням /25.2/ називають еліпсоїдом тензора.

Розглянемо, наприклад, тензор інерції . Як згадувалось раніше, недіагональні складові цього тензора характеризують вплив осі обертання на тіло, тобто, при 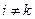тіло зазнає шкідливих впливів з боку осі обертання, воно деформується. Щоб уникнути таких шкідливих впливів треба, щоб обертання відбувалося навколо однієї з головних осей інерції, тобто однієї з осей еліпсоїда інерції.

6 + 3 = 9

/з підручника вищої математики

для футбольних тренерів/

26. Антисиметричні тензори другого рангу.

Нагадаємо, що тензор другого рангу називаємо асиметричним, якщо

-88-

/26.1/

З /26.1/ випливає, що

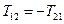
І матриця тензора набуває вигляду

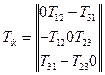/26.2/

- антисиметричний тензор другого рангу має три різні, відмінні від нуля компоненти.

Введемо позначення

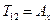
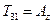
І переконаємось, що є компонентами псевдовектора. Для цього запишемо закон перетворення тензора

Тоді

/26.3/

-89-

Вирази для 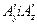знайдемо, використовуючи правило циклічної перестановки

/26.4/

/26.5/

У випадку перетворення інверсії

І тоді

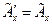
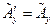
/26.6/

- величини 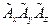дійсно перетворюються як складові псевдовектора.

Як тільки розв’язана одна проблема,

на її місце випливають нові проблеми.

Д.Гільберт

27. Диференціальні операції над тензорами.

Розглянемо тензорне поле – випадок, коли компоненти тензора є функціями координат точки

/26.1/у

Прикладами тензорних полів є:

скалярне поле

векторне поле

тензорне поле напружень у деформованому середовищі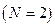

/кожній точці деформованого середовища відповідають свої значення складових тензора напружень/.

Розглянемо скалярне поле 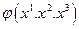і знайдемо три часткові похідні по координатах.

-90-

Як відомо, вони визначають коваріантний вектор градієнта скалярної функції. Таким чином, шляхом звичайного диференціювання ми можемо з тензора рангу одержати тензор рангу

Розглянемо тепер коваріантний вектор – функцію точки

і утворимо часткові похідні

Переконаємось, що дев ять величин /ми будемо називати їх мішаними похідними/ визначають коваріантний тензор другого рангу. При переході до нової системи

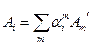
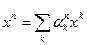
Отже, є коваріантним тензором.

Подібним чином можна переконатися що дев ять величин

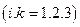
є компонентами мішаного тензора другого рангу. Це з рештою, випливає і з того, що мішані похідні /27.2/ і /27.3/ є мішаними добутками вектора і вектора /

Таким чином, шляхом мішаного диференціювання ми підвищуємо ранг тензора на одиницю – тензора рангу одержуємо тензор рангу .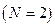

Згортаючи тензор /27.3/ ми одержимо тензор рангу - відомий вираз для дивергенції тензора

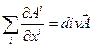
Різниця мішаних похідних

/27.3/

є антисиметричним тензором другого рангу 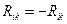, який, по суті, є ротором вектора .

Можна переконатися, що шляхом мішаного диференціювання можна підвищити на одиницю ранг довільного тензора. Часткові похідні від тензора рангу

/27.4/

-91-

є компонентами тензора рангу . Для цього треба вивчити трансформаційні властивості величин /27.5/. Зокрема, похідні 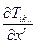визначають коваріантний тензор третього рангу.

Згорнемо тензор 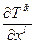по індексах і . Очевидно, резуль – вектор, позначимо його через .Тоді

/27.5/

або в проекціях на координатні осі

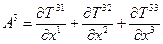/27.5/

Кожний з цих виразів нагадує вираз для дивергенції вектора /сума часткових похідних по координатах/, тому вектор –a називають векторною дивергенцією тензора. Рівність /27.6/ символічно можна записати

/27.5/

Векторна дивергенція тензора часто зустрічається в теоретичній фізиці /механіка деформованого середовища, електродинаміка, теорія відносності/.

Операції згортання і операції мішаного диференціювання є, в певному сенсі, протилежними. Перша понижує ранг тензора на дві одиниці, друга – підвищує ранг на одиницю. Це дає змогу побудувати тензор будь-якого рангу, якщо заданий тензор рангу .

Наприклад, застосовуючи операцію мішаного диференціювання, а потім згортання

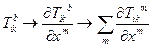
Як завжди, розв’язування однієї задачі породжує

нові. І останньої задачі ніколи не буде.

А.Смородинський

28. Криволінійні кординати.

До цього часу ми мали справу з декартовими або косокутними координатами. Положення точки зручно визначити за допомогою криволінійних координат.

-92-

Три координати називаються криволінійними координатами точки, якщо вони однозначно визначають положення точки в просторі.

Вони вводяться за допомогою системи рівнянь

/28.1/

Тобто

/28.1/

Рівняння /28.1/ можна розв’язати відносно

Функції /28.1/ і /28.2/ будемо вважати неперервними, диференційованими, а при необхідності – однозначними.

Приклад 1. Циліндрична система координат.

Циліндричними координатами точки М є

Вони зв’язані з декартовими координатами за допомогою відомих співвідношень

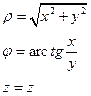
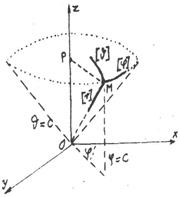
Приклад 2. Сферична система координат.

Сферичними координатами точки є

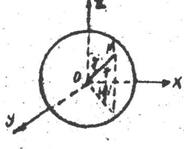
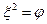
При цьому

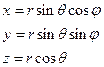
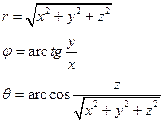
Приклад 3. Криволінійні координати точки задані рівняннм

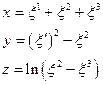
У першому з рівнянь /28.2/ зафіксуємо криволінійну координатну , тобто приймемо

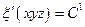
Очевидно, це є рівнянням певної поверхні в просторі , яку ми будемо називати координатною поверхнею. Існують всього три координатні поверхні.

-93-

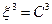
Вони перетинаються вздовж трьох ліній

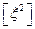
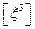
Які ми будемо називати координатними лініями.

Координатні лінії, в свою чергу перетинаються в одній точці М

Означення. Якщо три координатні лінії є взвємно перпендикулярними в кожній точці простору, то криволінійнап систеиа координат називається ортогональною.

Поверхня

Є циліндром радіуса , поверхня

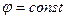
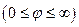
-площиною, яка проходить через вісь і утворює кут з площиною 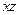поверхня

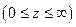
-площина, паралельна до площини 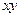на віддалі від цієї

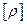
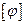
площини. Як видно з рис.73, три лінії є взаємо перпендикулярними.

Подібним чином переконуємось, що ортогональною є і сферична система координат. Координатними поверхнями є

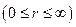
-сфера радіуса

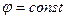
-94-

- площина що проходить через вісь і утворює кут з площиною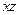

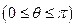
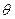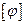
- конус, описаний навколо осі , твірна якого утворює кут з віссю . Як видно з рис. 74. три криві є ортогональними.

Дата добавления: 2015-05-24