Метричний тензор у косокутних координатах 6 страница

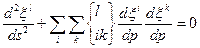/36.3/

У Декартові системі координат 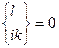і /36.6/ переходить у рівняння прямої лінії

,

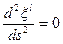Модель є не що інше, як спосіб особливо виділити деякі властивості, відповідальне явище, що розглядається

В.Вейскопф

37. Інтегрувальність афінного зв’язку

Евклідовими називаються такі простори, в яких можна ввести Декартові координати. Простір, заданий метрикою

-126-

є евклідовим, якщо існує таке перетворення координат

що

де

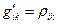
Прикладом неевклідового простору є двохвимірна крива поверхня, яку можна розглядати як підпростір у трьох марному просторі. Геометричні властивості цього підпростору можна розглядати незалежно від простору, в який він вкладений.

Виберемо, наприклад, плоский лист /евклідову двохмірну поверхню/ і розграфимо його в клітку. Змінимо тепер зв’язок цієї поверхні з трьохмірним простором – згорнемо лист. Лінії на ньому і далі утворюють декартову систему. В обох випадках

,

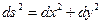Більше цього – лінії, що утворилися з прямих в результаті згортання і дальше залишаються лініяти найкоротшої віддалі. Таким чином, евклідовий характер простору залежить тільки від його метрики.

Розглянемо на площині елементарну площадку, визначену точками

Далі розглянемо вектор Aⁿ і визначимо його зміну при обході контура ABCDA.

У декартовій системі ми зустрінемось зі звичайними похідними 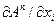. В узагальнених координатах звичайну похідну треба замінити на коваріантну

/37.1/

-127-

Зміна векторі Aⁿ на відрізках контура дорівнює:

1/ AB: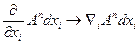

2/ BC: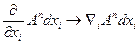

3/ CD:

4/ DA:

Комбінуючи /2/ і /4/ знайдемо різницю змін 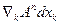в точках

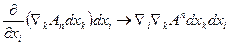
Аналогічно для /3/ і /1/ маємо

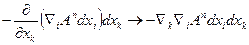
а повна абсолютна зміна вектора Aⁿ вздовж контура ABCDA буде

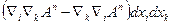/37.2/

Здавалось би, що цей вираз повинен дорівнювати нулеві. Однак, взагалі кажучи,

/37.3/

тобто результат коваріантного диференціювання залежить від порядку диференціювання.

Проаналізуємо це питання детальніше. Якщо ABCDA – прямокутник на площині /елемент плоского двохмірного простору/, то при паралельному перенесенні вектора Aⁿ вздовж контура його зміна дорівнюватиме нулеві

/37.4/

Нічого не зміниться, якщо замість декартових введемо криволінійні координати

/37.5/

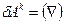
Якщо двохмірний простір викривлений /наприклад, ABCDA – елемент поверхні сфери/, то при паралельному перенесенні вздовж контура перенесений вектор Aⁿ не збігається з вихідним і тоді

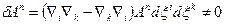/37.6/

-128-

Якщо перенесений паралельно вектор A вздовж довільної кривої збігається з вихідним, афінний зв’язок називається інтегрувальним /рис.81а/. У цьому випадку діє закон паралельного перенесення

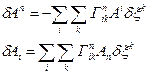
а для довільного замкненого контура С

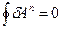/37.7/

У противному разі, коли перенесений паралельно вектор не збігається з вихідним, афінний зв’язок називається не інтегрувальним /рис.81б/ і тоді

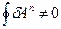/37.8/

Зрозуміло, що для плоских просторів / g_ik=const / афінний зв’язок завжди інтегрувальний, навіть, якщо замість декартових чи косокутних координат користуються більш складними змінними.

Любов приходить і відходить. Тензорний аналіз вічний.

/З розмови старших людей/

38. Тензор кривизни Рімана-Крістоффеля

Якщо афінний зв’язок простору інтегрувальний, то рівняння паралельного перенесення можна розглядати як рівняння в частинних похідних для векторного поля.

/38.1/

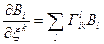/38.2/

-129-

Рівняння /38.1/ – перевизначенні: для визначення n компонент вектора маємо n² рівнянь /n – число вимірів простору/. Щоб система мала розв’язки, мусить задовольнятися ряд диференціальних тотожностей.

Візьмемо похідну по від /38.1/

Переставляючи індекси i,k, одержимо

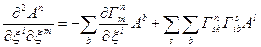
і тому

Вектор А довільний, Отже

/38.3/

- умова інтегрувальності афінного зв’язку.

Переконаємося, що для просторів з не інтегрувальним афінним зв’язком

Знайдемо різницю

За відомими правилами коваріантного диференціювання

-130-

Нам залишається підставити сюди вирази для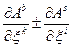

,

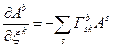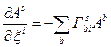
і, остаточно, ми маємо

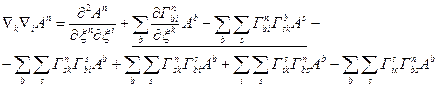
Вираз для ми одержимо з останньої рівності, переставляючи індекси i,k. Легке бачити, що при підрахунках різниці

більшість доданків скорочується. Доданки, що не скорочуються підкреслені хвилястою лінією в остаточній формулі. Пере позначимо нарешті, індекс сумування в доданку

тоді

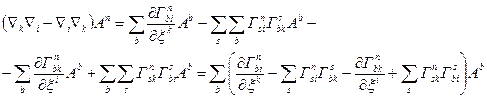
/38.4/

де

/38.5/

– тензор кривизни Рімана-Крістоффеля.

Перестановочні співвідношення для коваріантного диференціюван-

-131-

ня коваріантних векторів мають вигляд

/38.6/

що доводиться подібно, як /38.4/.

У метричному просторі тензор кривизни набуває вигляду

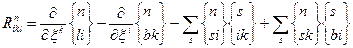/38.7/

Всі великі правди на початку є богохульством.

Б.Шоу

39. Властивості тензора кривизни

I. Тензор кривизни антисиметричний стосовно індексів i,k

/39.1/

Ця властивість автоматично випливає з /38.5/ і не залежить від властивостей симетрії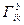

Якщо афінний зв’язок симетричний 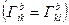то тензор має дальші властивості:

2. Сума компонент тензора кривизни, що отримується при циклічній перестановці перших трьох індексів, дорівнює нулеві

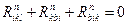/39.2/

Доведення проводиться безпосереднім підрахунком за формулою /38.5/.

3. Виведеио т.зв. тотожності Б’янкі.

Від обох сторін рівності

візьмемо коваріантну похідну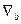

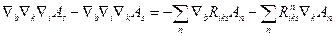
Перепишемо цю рівність ще два рази, змінюючи циклічно індекси i,k,l

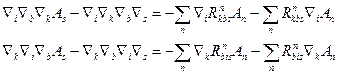
Додамо всі три рівності і згрупуємо доданки

/39.9/

-132-

Перетворимо вирази, що стоять у дужках. Позначимо

Згадаємо перестановочні співвідношення

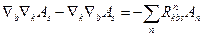
і запишемо їх для коваріантного тензора другого рангу

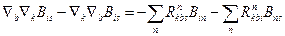
Якщо , то

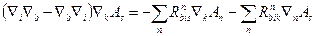
Підставимо ці вирази в /39.3/ і враховуємо /39.2/. Після скорочення одержимо тотожності Б’янкі

/39.4/

Введемо тепер коваріантний тензор кривизни в метричному просторі шляхом опускання контраваріантного індекса

/39.5/

Знайдемо формулу, яка дозволяє виразити R_iklm через символи Крістоффеля першого роду.

Використаємо допоміжну формулу

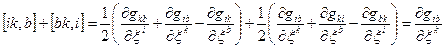
Перший доданок /38.7/ запишеться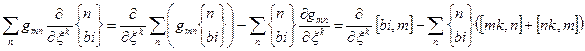

і аналогічно другий

-133-

Тензор R_iklm можна тоді записати у вигляді

Замінимо тут символ Крістоффера другого роду символами першого роду

,

тоді R_iklm набуде вигляду

або, остаточно, перепозначуючи німі індекси r і s в третій групі доданків

Щоб знайти інший вираз для R_iklm розкриємо формули для [bi,m] і [lk,m]. Тоді

-134-

Підставимо ці вирази в /39.6/. Після скорочення одержимо

/39.7/

Звідси зразу видно, що R_iklm антисиметричний стосовно останніх двох індексів

/39.9/

Для коваріантного тензора справедлива і рівність /39.2/

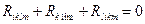/39.10/

Трагедія людства полягає в тому, що воно розв’язує проблеми Космосу, не розв’язавши ще земних проблем.

Дж.Стейнбек

40. Згортання тензора кривизни

З допомогою операції згортки тензора можна одержати тензори другого рангу

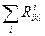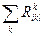, , , /40.1/

Всі інші згортки дорівнюють нулеві завдяки /39.8/ - /39.10/.

Наприклад,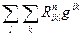

дорівнює нулеві як згортка антисиметричного тензора з симетричним.

Всі тензори /40.1/ рівні з точністю до знака. Наприклад,

-135-

завдяки рівності

Введемо позначення

/40.2/

/тензор Річчі/. Згортаючи цей тензор, отримаємо скалярну кривизну

/40.3/

Згідно з загальною формулою

ми маємо

/40.4/

Тензор R_kb симетричний. Симетрія останніх трьох доданків у /40.4/ очевидна, тому розглянемо перший доданок

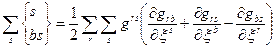
Різниця є антисиметричним виразом відносно r і s його згортка з симетричним тензором дорівнює нулеві. Залишається

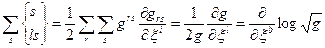
де g – детермінант, побудований з g_ik. Тому

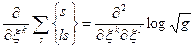
а вираз цей симетричний відносно r,l. Таким чином

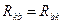/40.5/

Виведемо тепер т.зв. згорнені тотожності В’янжі. Рівність

/ми чітко вказуємо точками місця, на які будемо піднімати або опускати індекси/ згорнемо по індексах i,n

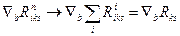
-136-

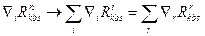
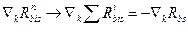
тоді

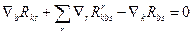
Обидві сторони цієї рівності помножимо на g^ms і просумуємо по s. Відповідно доданки дорівнюють

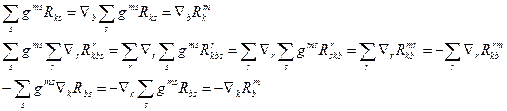
Збираючи доданки одержимо

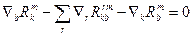
Згорнемо цю рівність по індексах k,m

отже,

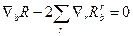
Одержану рівність помножимо на g^bs і просумуємо по l

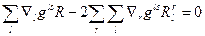
і остаточно

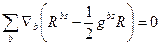/40.6/

Вираз, що стоїть в дужці, звичайно позначають через G^bs

/тензор Ейнштейна/

-137-

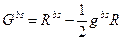/40.7/

Отже,

/40.8/

– коваріантна дивергенція тензора Ейнштейна дорівнює нулеві. Ця рівність і є записом згорнених тотожностей Б’янкі.

У релятивістській космології розглядаються більш загальний вираз для тензора Ейнштейна

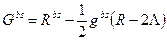/40.9/

де 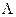– стала величина /космологічна стала/. Очевидно, тензор /40.9/ також задовольняє згорнені тотожності Б’янкі, тому що коваріантна поідна від метричного тензора дорівнює нулеві.

Запишемо ще коваріантний і мішаний тензори Ейнштейна

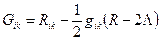/40.10/

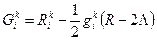/40.11/

при цьому

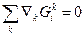/40.12/

Тому тензори R_ik і g_ik симетричні, то і тензор G_ik є симетричним.

Метафізика: Шукання в абсолютно тамній кімнаті чорного кота, який знаходиться в іншому місці.

М.Метерлінк

41. Число незалежних компонент тензора кривизни

Доведемо, що число незалежних компонент тензора кривизни в мірному просторі визначається формулою

/41.1/

Розділимо компоненти R_iklm на три групи:

1. Компоненти, в яких різні лише два індекси: Перші і другі пари індексів повинні збігатися попарно, а два індекси одної пари збігатися не можуть, тому що

-138-

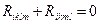
Кількість складових такого типу, тобто складових R_ikik /складові R_ikki відрізняються лише знаком/, дорівнює числові пар (i,k) при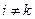

Множник 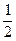появився тому, що послідовність i,k не має значення.

2. Компоненти, які мають три різні індекси: всі вони зводяться до вигляду R_iklm.

Індекс i набуває n значень. З решти n-1 значень треба вибрати пари різних значень для k і m. Це можна зробити способами, тому

.

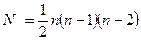3. У компонентах третьої групи вся чотири індекси різні (R_ikbm). Першу пару індексів можна вибрати способом. Залишається n-2 чисел інших індексів, цю пару можна вибрати 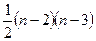способами. Тому що послідовність обох пар не має значення 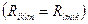результат треба ще розділити на 2. Тому

Коефіцієнт ми поставили, враховуючи тотожність

Повне число алгебраїчно незалежних компонент дорівнює

тобто

У двохмірному просторі (n=2)

N=1

– один скаляр R повністю характеризує кривизну.

У трьохмірному просторі N=6 /стільки компонент має R_kl /.

В чотирьохмірному просторі

N=20

а число згорнених компонент дорівнює 10. Тому при кривизна простору повністю визначається згорненим тензором

-139-

Якщо хочеш бути щасливим три години – випий півлітри /кефіру/, якщо хочеш бути щасливим три дні – одружися, якщо хочеш бути щасливим три тижні – заколи порося і з’їж його, якщо хочеш бути щасливим все життя – вивчай тензорний аналіз.

/Підслухане/

42. Тензорний характер законів фізики

На початку згадаємо деякі факти, відомі з елементарної фізики.

Розглянемо рівняння

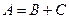/42.1/

де A,B,C – якісь фізичні величини. Очевидно, що всі три величини мусять мати однакову розмірність. Наприклад А вимірюється в метрах, то таку ж розмірність порвинні мати і величини В, С. Інша справа, що в рівності

величини А, В, С можуть мати різну розмірність.

Звернемо увагу ще на одну властивість фізичних законів. Якщо закон задається рівнянням

А=В,

то величини А і В повинні мати однакову «тензорну розмірність». Ц означає, що якщо А є скаляром, то і величина В також є скаляром. Якщо А є вектором, то і В є вектором. Зрозуміло, що це правило поширюється і на тензори вищих рангів. У рівнянні

/42.2/

тензори T i U мусять бути тензорами одного і того ж рангу, число ко­– і контраваріантних індексів повинні бути відповідн однаковими. Лише у такому випадку можна сподіватися, що закон фізики буде справедливий в усіх системах координат.

Як приклад розглянемо закон Гука з механіки деформованого середовища

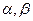Тут – тензор напружень, – тензор деформацій, – коефіцієнти, що характеризують пружні властивості речовини, – об’ємна дилатація. Всі доданки мають однакову тензорну розмірність – – коваріантні симетричні тензори другого рангу.

Сформульований нами принцип має велику евристичну силу. Якщо

-140-

якийсь закон фіфзики справедливий в одній системі координат /чи в одному класі координатних систем/, то шляхом перетворення координат ми можемо знайти більш загальний закон, справедливий в усіх системах.

Проілюструємо це на прикладі з теоретичної механіки.

Як відомо, другий закон механіки

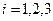/42.3/

в справедливим лише в інерціальних системах координат. Нагадаємо, що інерціальною системою 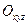називається така система, в якій точка, на яку не діють жадні сили, рухається прямолінійно і рівномірно.

Розглянемо систему , що рухається прямолінійно і рівномірно стосовно інерціальної системи . Тоді

,

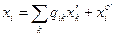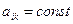
Компоненти вектора перетворюється за таким же законом, що й координати

.

Тому що

,

рівняння /42.3/ набуває вигляду

а звідси випливає, що

/42.4/

– другий закон механіки справедливий в усіх інерціальних системах координат.

Розглянемо випадок, коли початки систем і збігаються / /, але – система обертається навколо точки 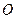. Тоді 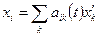, , 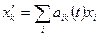звідки

-141-

,

.

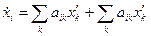Рівняння /42.4/ набуде вигляду

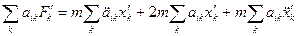
Обидві сторони рівності помножимо на і просумуємо і

Дата добавления: 2015-05-24