Метричний тензор у косокутних координатах 7 страница

Враховуючи, що

,

і користуючись правилом підстановки індекса, ми одержимо

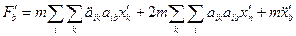
– другий закон механіки в неінерціальній системі .

Перетворимо другий доданок у правій частині /42.5/. Про диференціюємо по часі умову

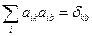
одержимо

Звідси випливає, що

,

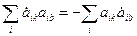і тоді

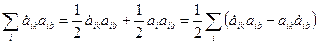
Вираз

/42.6/

називають тензором кутової швидкості. Це антисиметричний тензор другого рангу, що має шість істотно різних складових

-142-

Рівняння (42.50) набувають вигляду

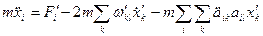. (42.7)

Таким чином, в неінерціальній системі координат крім сили , на точку діють ще дві додаткові сили:

сила К, що має проекції

і називається силою Коріоліса,

сила , проекції якої дорівнюють

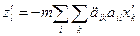
і яку називають відцентровою силою.

Легко переконатися, що вектори сили Коріоліса перпендикулярний до вектора швидкості точки стосовно рухомої системи. Для цього обчислимо скалярний добуток двох векторів

.

Одержаний вираз є подвійною згорткою симетричного тензора і антисиметричного тензора 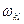. Такий вираз дорівнює нулеві і тому .

У спеціальному випадку, коли ос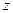і і обох систем збігаються, а система рівномірно обертається навколо осі z з кутовою швидкістю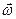

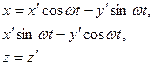
Коефіцієнти перетворення і їх похідні визначаються матрицями

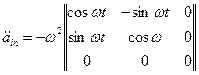
тому

-143-

, , ,

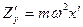а проекції Коріоліса на осі рухомої системи дорівнюють

,

, .

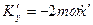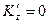При перетворенні подібного типу потрібна особлива обережність. Відомо, наприклад, що теорема моментів для руху твердого тіла навколо рухомої точки

,

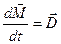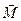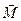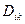де – момент кількості руху тіла, – головний момент зовнішніх сил, справедлива лише в інерціальних системах. Щоб записати закон в будь-якій неінерціальній системі, треба врахувати, що і в аксіальними векторами, тобто псевдовекторами. Їх треба розглядати як антисиметричні тензори і . Рівняння (42.8) треба записати у вигляді

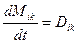
Дальше переходять від інерціальної системи до інерціальної системи , зв’язаної з твердим тілом. В результаті одержується відоме рівняння Ейлера для руху твердого тіла навколо нерухомої точки

У природі немає превілейованих систем координат (для простоти ми не розрізняємо поняття «система координат» від поняття «система відліку»). Всі інерціальні системи рівноправні з точки зору релятивістської механіки і електродинаміки. Неінерціальні системи також придатні до запису законів фізики. З другого боку, як ми бачили на прикладі другого закону механіки, один і той же закон записується, взагалі кажучи, по різному в різних системах координат. Тому перед фізиками стоїть принципово важлива задача: записати закони природи в такому вигляді, який був би одинаковий на всіх сиcтемах.. рівняння, вигляд яких не залежить від вибору сиcтеми координат, називається коваріантними, запис таких рівнянь – коваріантним.

-144-

Тензорні методи дозволяють записати закони природи в коваріантній – тензорній формі. Цю програму вдалося чітко реалізувати в усіх розділах теоретичної фізики, знайдено строгі правила узагальнення звичайних рівнянь на тензорні рівняння, які не змінюють свого вигляду при переході від однієї системи до іншої.

Наведемо приклад. Як відомо, багато законів фізики записуються у вигляді диференціальних рівнянь. Однак, звичайна похідна від тензора не має тензорної розмірності, не є тензором. Якщо рівняння має вигляд

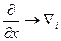
(пор. (37.1.) і рівняння

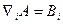
вже є тензором.

Зміст

ВЕКТОРНИЙ АНАЛІЗ

1. Перетворення прямокутних координат точки

2. Перетворення компонент вектора при переході від одної прямокутної системи до іншої

3. Елементи вищої алгебри

4. Псевдовеличини

5. Вектор–функція скалярного аргумента

6. Скалярне і векторне поле. Градієнт скалярного поля

7. Похідна від вектора по напрямку

8. Потенціальне векторне поле. Лінійний інтеграл від вектора

9. Потік вектора через поверхню. Дивергенціал вектора

10. Теорема Остроградського–Гаусса

11. Рівняння Лапласа

12. Ротор вектора

13. Теорема Стокса

14. Деякі формули векторного аналізу

15. Соленоїдальні поля

ТЕНЗОРНИЙ АНАЛІЗ

16. Косокутні системи координат. Узагальнені проекції та узагальнені складові вектора. Дуальна система координат

17. Метричний тензор у косокутних координатах

18. Скалярний і векторний добуток двох векторів в косокутних координатах

19. Правила індексів

20. Диференціал операції в косокутних координатах

21. Перетворення координат і компонент вектора при переході від одної косокутної системи до іншої

22. Скаляри, вектори і тензори в косокутній системі координат

23. Приклади тензорів

24. Згортання тензорів

25. Деякі властивості симетричних тензорів другого рангу

26. Антисиметричні тензори другого рангу

27. Диференціальні операції над тензорами

28. Криволінійні координати

29. Метричний тензор в криволінійних координатах

30. Тензори в криволінійних просторах

31. Метричні простори

32. Задача про паралельне перенесення вектора

33. Символи Крістоффеля. Класифікація просторів

34. Коваріантне диференціювання

35. Диференціальні операції в метричних просторах

36. Геодизичні лінії

37. Інтегрувальність афінного зв’язку

38. Тензор кривизни Рімана–Крістоффеля

39. Властивості тензора кривизни

40. Згортання тензора кривизни

41. Число незалежних компонент тензора кривизни

Тензорний характер законів фізики

Дата добавления: 2015-05-24