Границя і неперервність функції

Поняття функції

Розділ 4. Неперервні відображення

Означення 1.1. Нехай маємо дві множини Х і У. Якщо кожному елементу за певним законом ставиться у відповідність один і тільки один елемент у із множини У, то говорять, що на множині Х задана функція f (або відображення множини Х в множину У).

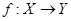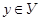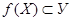Записують так: . Якщо у відповідає х, то записують так: . Множина Х називається областю визначення функції f. Множина тих , які приймає функція, називається областю значень функції , – область значень, (не обов’язково ). Якщо 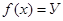, говорять, що функція відображає множину Х на множину У.

Через 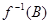будемо позначати прообраз множини (це множина А всіх тих х -ів з Х, що ).

Нехай маємо два метричні простори Х і У. Відстань в просторі Х будемо позначати r, в просторі У –r₁.

Нехай множина М міститься в Х, 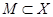, на множині М задана функція 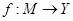, яка відображає множину М в У, гранична точка множини М.

Означення 2.1. Елемент b простору У, називається границею функції f, коли х прямує до , якщо для довільного існує 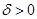таке, що для будь-якого х із множини М, яке задовольняє умові 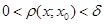, виконується нерівність: .

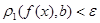Дане означення евівалентне наступному.

Означення 2.2. Елемент b простору У, називається границею функції f, коли х прямує до , якщо для довільної послідовності вилученої з М, причому 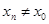, яка збігається до , відповідна послідовність значень функції 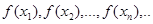збігається до b.

Еквівалентність обох означень доводиться як і для дійсних функцій.

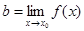Якщо b – границя функції f при х, прямуючому до , то записують так: , іноді пишуть 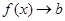, коли . Якщо 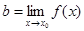, то це геометрично означає, що який би ми окіл точки b не взяли, то знайдеться проколотий окіл точки х₀ такий, що якщо х попаде в цей проколотий окіл, то f(x) попадає у вибраний окіл точки b (проколотий окіл точки х₀ – це окіл точки х₀ з якого вилучено точку х₀).

Означення 2.3. Функція f, ,називається неперервною в точці 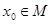, якщо для довільного , існує 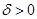, таке, що для всіх х з множини М, які задовільняють умові 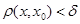, визначається нерівність .

Якщо 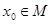є граничною точкою множини М, то це означення еквівалентне наступному.

Означення 2.4. Функція f називається неперервною в точці 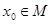, якщо .

Еквівалентність обох означень для цього випадку очевидна.

Означення 2.5. Функція f, яка відображає множину М метричного простору Х в метричний простір У, називається неперервною на множині М, якщо вона неперервна в кожній точці цієї множини.

Означення 2.6. Функція f, , називається рівномірно неперервною на множині М, якщо для довільного , існує таке 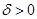, що для будь-яких х ₁ і х ₂ із множини М, які задовольняють умові , виконується рівність .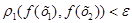

Якщо f рівномірно неперервна на М, то вона і неперервна на цій множині. Обернене твердження взагалі невірне.

Теорема 2.1. (Критерій неперервності). Для того, щоб відображення f:X®Y було неперервним в Х, необхідно і достатньо, щоб прообразом будь-якої відкритої множини простору У була відкрита множина простору Х.

Доведення.Необхідність. Нехай f неперервне відображення і G відкрита множина простору У, f ^–1(G) прообраз G. Якщо f ^–1(G) є порожньою множиною, то все зрозуміло, бо порожня множина є відкритою множиною. Нехай f ^–1(G)¹Æ і х₀Î f ^–1(G). Тоді у ₀= f(x ₀ )Î G. Оскільки G відкрита множина, то існує e-окіл S(y₀; e ) точки у₀, який повністю лежить в G. Так, як відображення f неперервне в точці х ₀, то існує d-окіл цієї точки такий, що для всякого х з цього околу, f(x) належить S(y ₀ ,e). Отже всі точки d-околу точки х ₀ належать f ^–1(G), а це означає, що х ₀ внутрішня точка f ^–1(G), а f ^–1(G) є відкритою множиною.

Достатність. Нехай прообразом будь-якої відкритої множини є відкрита множина. Покажемо, що f неперервна функція в G. Нехай х ₀Î Х, у ₀= f (x ₀)Î Y. Візьмемо довільний e-окіл S(f(x ₀ ),e) точок f(x ₀ ). Оскільки він є відкритою множиною, то його прообразом є відкрита множина, яка містить точку х ₀. Тому існує d-окіл S(x ₀,d ) точки х ₀, який повністю міститься в f ^–1(G). А це означає, що f є неперервною функцією в точці х ₀, а отже і в просторі Х. Теорему доведено.

Дата добавления: 2015-05-24