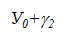Існування неявної функції однієї змінної

Розділ 4. Неявні функції

Розглнемо криву х²+у²= 1, це є коло.

Зрозуміло, що якщо точка М₀ належить колу і не належить його горизонтальному діаметру, то завжди можна знайти окіл точки такий, що в ньому дане рівняння задає єдину функцію у від х, що визначена на проекції цієї дуги на вісь ОХ, тобто "х, що належить проекції $! у(х):х²+у(х)²= 1. Будемо казати, що рівняння х²+у²= 1 задає неявну функцію у від х.

Нехай функція F(x;y) визначена на множині ЕÌR² і Х – проекція цієї множини на вісь ОХ.

Будемо говорити, що рівняння F(x;y)=0, задає у, як функцію від х, у=f(х) на множині Х, якщо "хÎХ існує пара (х;f(x))ÎЕ, яка задовільняє рівняння F(x;y)=0, тобто F(x;f(x))=0 є тотожністю на множині Х.

В нашому прикладі , .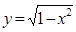

Ми бачимо, що в околі точки М₀ це рівняння задаває єдину функцію у(х), щоб знайти її явне вираження, ми розв’язали наше рівняння відносно у. Та це вдасться зробити не завжди. Одже виникає така задача: як маючи певні властивості функції F, прогнозувати існування цієї неявно заданої функції, а також, які властивості повинна мати F, щоб ця неявно задана функція була, наприклад, неперервною чи диференційовною.

Зауважимо, що навіть на нашому простому прикладі видно, що якщо ми візьмемо т. М₀( 1, 0 ), то такої єдиної визначеної функції, як вище вже не буде. Якщо ми спроектуємо будь-який окіл цієї точки М₀ на ОХ, то помітимо, що на інтервалі, що належить проекції цього околу, рівняння кола задає безліч функцій у(х).

Теорема 1.1. Нехай:

1) функція F(x;y) неперервна разом із своїми частинними похідними F¢_x і F¢_y в деякому уколі т. М₀(х₀,у₀);

2) F¢_y в точці (x₀;y₀) не дорівнює нулю;

3) F(x₀;y₀)=0.

Тоді в деякому прямокутнику П={(x;y) x₀-g ₁ <x<x₀+g ₁, y₀-g₂<y<y₀+g₂ }, рівняння F(x;y)=0 задаватиме єдину функцію у=f(x), яка задовільняє наступним умовам:

1) ця функція буде неперервною на інтервалі (х₀-g ₁ ;x₀+g ₁);

2) на цьому інтервалі існує f¢(x), яка буде неперервною.

Доведення. Нехай . З умов 1,2 теореми випливає, що $ деякий окіл т. М₀, такий, що для всіх точок М, з цього околу, F(x;y) буде диференційовною і F¢_y(x;y)>0

х₀+g₁

х₀-g₁

У₀+g₂

Впишемо в цей окіл замкнений прямокутник з центром в точці М₀, сторони якого паралельні до координатних осей. Проведемо через т. М ₀ відрізок в прямокутнику паралельний до ОУ, розглянемо функцію F¢_y(x;y). В точках відрізка АВ вона матиме вигляд F¢_y(x₀;y) ( вона є похідною від функції F(x₀;y) по змінній у). Оскільки F¢_y(x₀;y)>0 і y₀-g₂£y£y₀+g₂, то функція F(x₀;y) є монотонно зростаючою на сегменті [ y₀-g₂; y₀+g₂ ]. Звідси і з того, що F(x₀, y₀)=0 одержуємо, що F(x₀, y₀-g₂)<0, F(x₀;y₀+d)>0 тобто, інакше кажучи, F(A)<0, F(B)>0. Так, як функція F(x,y) є неперервна в точці А і в точці В (тому що обидві ці точки належать околу де вона є неперервною), то існують окіл точки А і окіл точки В такі, що в межах першого F(x;y)<0, а другого F(x;y)>0. Не зменшуючи загальності, можна вважати, що радіуси цих околів рівні. Якщо радіус цього околу g ₁, то із вище сказаного слідує, що для будь-якого х, який належить (х₀-g ₁, х₀+g ₁), F(x,y₀-g₂)<0, a F(x,y₀+g₂)>0.

Візьмемо будь-яке х, яке належить (х₀-g ₁ ;х₀+g ₁) і проведемо через це х пряму, перпендикулярну до ОХ. Оскільки точка А¢ лежить на відрізку А ₁ А₂, а в кожній точці цього відрізка F(x;y)<0, то F(A¢)<0. Аналогічно F(B¢)>0.

Розглянемо функцію F(x;y) на відрізку А¢В¢. На цьому відрізку вона є функцією однієї змінної у (бо тут х зафіксоване). При цьому вона буде неперервною на [ y₀-g₂;y₀+g₂ ] і строго зростаючою. Оскільки в лівому кінці інтервала вона приймає від’ємне значення, а в правому – додатнє, то із всього сказаного вище випливає (за теоремою Больцано-Коші), існування єдиного у із інтервала (y₀-g₂;y₀+g₂) такого, що F(x;y)=0.

Таким чином ми встановили, що на інтервалі (х₀-g ₁ ,х₀+g ₁) існує єдина функція y=f(x) така, що F(x,f(x))=0 на цьому інтервалі.

Покажемо, що функция f(x) неперервна на інтервалі (х₀-g ₁ ,х₀+g ₁). Нехай хÎ (х₀-g ₁ ,х₀+g ₁). Дамо х приріст Dх. Тоді функція одержить приріст Dy.

Точки (x;y) і (х+Dх;y+Dy), де y=f(x), y+Dy=f(x+Dy) задовільняють рівнянню F(x;y)=0. Таким чином

DF(x;y)=F(х+Dх;y+Dy)-F(x;y)=0.

Використовуючи теорему Лагранжа, одержимо:

0= F(х+Dх;y+Dy)-F(x;y)=(F(х+Dх;y+Dy)-F(x;y+Dy))+(F(x;y+Dy)-F(x;y))=

=F¢_x(x+qDx;y+Dy)Dx+F¢_y(x;y+q ₁ Dy)Dy,

де 0< q< 1, 0< q ₁ < 1. Так, як F¢_y≠0, то

(1.1).

Оскільки F¢_x і F¢_y неперервні у замкнутому прямокутнику і F¢_y >0, то існують М>0 і т>0 такі, що ½ F¢_x ½≤ M і F¢_y > m.

Таким чином 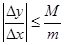. Звідси маємо 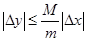. Якщо Dх®0, то Dy®0, а це і означає, що f(x) неперервна в точці х.

Покажемо, що існує похідна f¢(x) для будь-якого хÎ (х₀-g ₁ ,х₀+g ₁). Нехай хÎ (х₀-g ₁ ,х₀+g ₁). Надамо х приріст Dх. Тоді функция одержить приріст Dу. Якщо Dх®0 то і Dу®0. При цьому , де 0< q< 1, 0< q ₁ < 1. Враховуючи, що F¢_x і F¢_у неперервні і F¢_у≠0, перейшовши до границі, коли Dх®0, одержимо:

.

А це і означає, що похідна в точці х існує і

.

Крім цього, як випливає з останньої формули, 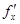є неперервна на інтервалі (х₀-d;x₀+d) тому, що чисельник і знаменник останньої рівності є композиція неперервних функцій і 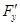і у=f(x). Теорему доведено.

Дата добавления: 2015-05-24