Достатні умови існування екстремуму

Розглянемо достатні умови існування екстремуму.

Теорема 3.1 Нехай функція U=f(x ₁, x₂,…, x_n) має в деякому околі стаціонарної точки М₀ частинні похідні до 2-го порядку включно, причому вони неперервні в точці М₀. Тоді, якщо в точці М₀ диференціал 2-го порядку цієї функції є знаковизначеною квадратичною формою, то в цій точці функція має екстремум: максимум, якщо ця форма від’ємно визначена та мінімум, якщо-додатньо визначена. Якщо диференціал 2-го порядку в цій точці є знакозмінною квадратичною формою, то екстремуму в точці М₀ немає.

Доведення. З умови теореми маємо, що наша функція двічі диференційовна в деякому околі точки М₀. Тому для будь-якої точки М з цього околу за формулою Тейлора матимемо, що

,

при цьому , N –проміжна точка з координатами N=(x⁽⁰⁾ ₁ +q ₁ Dx ₁; x⁽⁰⁾₂+q₂Dx₂,…, x⁽⁰⁾_n+q_nDx_n), де 0<q₁<1,…,0<q_n<1.

,

де , коли (Dх₁,...,Dх_п)®(0,...,0).

Нехай тоді

.

Розглянемо поведінку множника в другому доданку при r²: коли (Dх₁,...,Dх_п)®(0,...0).

Таким чином 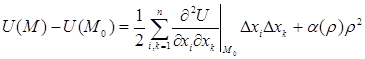, де a(r)®0, коли r®0.

Отже ми тільки що довели, що для будь-якої точки М справедлива рівність:

(3.1).

Перетворимо перший доданок останньої рівності:

= ,

де , ½ h_i ½£1 і h₁²+…+h_n²=1.

Звідси і з (3.1) будемо мати:

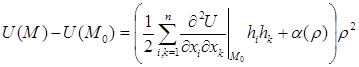(3.2).

Нехай диференціал 2-го порядку в точці М₀ є додатньо визначеною квадратичною формою. Оскільки диференціал 2-го порядку в точці М₀ дорівнює добутку першого доданка справа в (3.2) без множника , то цей доданок теж є додатньо визначеною квадратичною формою заданою на одиничній сфері простору Rⁿ. Оскільки ця квадратична форма є функцією неперервною на цій точці, а сфера Rⁿ є компактом (бо вона замкнена і обмежена) то за теоремою Вейєрштрасса на цій сфері знайдеться точка (h₁⁽⁰⁾,…,h_n⁽⁰⁾) в якій ця квадратична форма приймає найменше значення m. Оскільки форма додатньо визначена, то m>0. Отже перший доданок справа в (3.2) завжди більший або рівний m/2. Оскільки a(r)®0 коли r®0 то знайдеться r ₁ >0: "r£r ₁ матимемо: ½ a(r) ½< m/4.

Візьмемо . Тоді будемо мати .

Отже ми довели, що U(M)>U(M₀) для будь-якої точки М з r₁-околу точки М₀, а це означає, що в точці М₀ функція має мінімум (для максимуму доведення аналогічне).

Розглянемо доведення 2-ї частини теореми. Для цього зробимо кілька зауважень відносно квадратичної форми.

Якщо Ф(t ₁ ,…,t_n) деяка знакозмінна квадратична форма, то можна підібрати дві точки h¢=(h ₁ ¢,…,h_n¢), h¢¢=(h ₁ ¢¢,…,h_n¢¢) такі, що ½ h_i¢ ½£1; ½ h_i¢¢ ½£1, 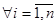; h ₁ ¢ ² +…+h_n¢ ² = 1; h ₁ ¢¢ ²+…+h_n¢¢ ²= 1і Ф(h¢)>0, Ф(h¢¢)<0. Дійсно, оскільки Ф знакозмінна квадратична форма, то знайдуться дві точки t¢=(t ₁ ¢,…,t_n¢), t¢¢=(t ₁ ¢¢,..,t_n¢¢): Ф(t¢¢)>0, Ф(t¢¢)<0. Покладемо

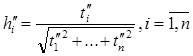, , ми одержимо h¢ і h¢¢ такі, що задовольняють умови і ;.

Візьмемо довільне d>0. Нехай h¢=(h¢ ₁,…, h¢¢ _n ) така точка на одиничній сфері, що . Візьмемо точку таку, що , а значить . Тоді

_.

Оскільки a(d)®0, коли d®0, а перший доданок є додатнім і не залежить від d, то можна підібрати d настільки малим, що вираз в дужках зберігатиме знак першого доданка. Тобто ми в як завгодно малому околі точки М₀, знайшли точку М¢, таку що U(M¢)-U(M₀)>0. Провівши аналогічні дослідження для U(M¢¢)-U(M₀), ми отримаємо, що в як завгодно малому околі точки М₀ знайдеться точка М¢¢, значення функції в якій менше за значення в точці М₀. Отже в точці М₀ функція не має екстремуму. Теорему доведено.

Часто виникає потреба дослідити на екстремум функцію двох змінних. Розглянемо цей випадок.

Теорема 3.2 (Достатні умови існування екстремуму для функції 2-х змінних). Нехай функція U=f(x;y) має частинні похідні другого порядку в деякому околі стаціонарної точки М₀, які неперервні в цій точці. Нехай а ₁₁ =f_xx¢¢(M₀); а₂₂=f_yy¢¢(M₀); а ₁₂ =f_xy¢¢(M₀) і D(М₀)=а ₁₁ а ₂₂ -а ₁₂². Якщо D(М₀)>0, то в точці М₀ функція U має екстремум, а саме мінімум, коли а ₁₁>0 і максимум, коли а ₁₁<0. Якщо D(М₀)<0 то екстремуму в точці М₀ дана функція немає.

Доведення. Перша частина теореми слідує з теореми 3.1 і критерію Сільвестера знаковизначеності квадратичної форми, бо А ₁= а ₁₁, А₂ = а ₁₁ а₂₂-а ₁₂². Тому, якщо D М₀>0, то d²U є знаковизначеною квадратичною формою, а саме, якщо а ₁₁ >0 додатньо визначеною і при а ₁₁ <0 – від’ємно визначеною. А значить, якщо а ₁₁ >0 функція має мінімум, а при а ₁₁ <0 – максимум.

Розглянемо випадок коли D(М₀)<0. На основі доведеного в теоремі 3.1, квадратичну форму диференціала в точці М₀ можна записати у вигляді: Ф=(a ₁₁ h ₁ ²+2a ₁₂ h ₁ h ₂ +a₂₂h ₂² ), де h ₁ ²+h₂²= 1. Покажемо, що в цьому випадку квадратична форма 2-го диференціала в точці М₀ є знакозмінною. Для цього достатньо знайти дві точки h¢=(h ₁ ¢,h₂¢), h¢¢=(h ₁ ¢¢,h₂¢¢) на одиничному колі такі, що в одній із них форма Ф буде додатньою, а в іншій – від’ємною величиною.

Нехай а ₁₁ ¹0, тоді

Ф(h ₁ h₂)= 1/ a ₁₁ (a ₁₁ ²h ₁ ²+2a ₁₁ a ₁₂ h ₁ h₂+a ₁₂ ²h₂²+a ₁₁ a₂₂h ₂² - a ₁₂ ²h₂²)=

= 1/ a ₁₁ ((a ₁₁ h ₁ +a ₁₂ h₂)²+(а ₁₁ а₂₂-а ₁₂ ²)h₂²)

Якщо h ₁ = 1; h₂=0, товираз в дужках додатній. Якщо візьмемо 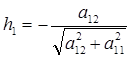і , то одержимо точку, яка лежить на одиничному колі і для якої вираз в дужках є від’ємним. Отже наш диференціал 2-го порядку є знакозмінною квадратичною формою, коли а ₁₁ ¹0.

У випадку, коли а ₁₁ =0, Ф(h ₁ ,h₂)= (2 a ₁₂ h ₁ h₂+a₂₂h₂²) = (2 a ₁₂ h ₁ +a₂₂h₂) h₂. Підберемо h ₁; h₂ так, щоб ½2 а _{1 2} h ₁½>½ a₂₂h₂ ½, h ₁²+ h ₂²=1. Тоді величини 2 а ₁₂ h ₁ +a₂₂h₂ і 2 a ₁₂ h ₁ +a₂₂(-h₂) матимуть один і той самий знак, а значить (2 a ₁₂ h ₁ +a₂₂h₂) h₂ і (2 a ₁₂ h ₁ +a₂₂(-h₂)) (- h₂) матимуть різні знаки. Це означає, що квадратична форма не є знаковизначеною. На основі попередньої теореми екстремуму в точці М₀ немає. Теорему доведено.

Дата добавления: 2015-05-24