Алгебраические критерии устойчивости

Решение линейных дифференциальных уравнений с постоянными коэффициентами классическим методом

Математические методы исследования

Системы уравнений возмущённого движения (11.4), (11.5) и (11.6) являются неоднородными линейными дифференциальными уравнениями в общем случае с переменными коэффициентами. В случае, если в правую часть явно не входит независимая переменная t и производные в правой части этих уравнений изменяются незначительно, то их принимают постоянными на маленьком отрезке времени (в соответствии с “методом замороженных коэффициентов ”) и системы уравнений становятся системами дифференциальных уравнений с постоянными коэффициентами. При в уравнении (11.4) система становится однородной и описывает собственное возмущенное движение ЛА. Такое движение можно получить, если находящемуся в равновесном режиме полета ЛА сообщить некоторые начальные возмущения, а затем предоставить самому себе.

Если в полете ЛА будет подвергаться постоянно действующим возмущениям, то его возмущенное движение будет описываться системой неоднородных уравнений, правые части которых представляют собой некоторые известные функции времени. Такими функциями могут быть внешние силы, вызванные управляющими воздействиями или какими-либо другими возмущениями, например, ветровыми.

Известно, что общее решение системы линейных неоднородных дифференциальных уравнений состоит из общего решения соответствующей системы однородных уравнений и частного решения полной (неоднородной) системы.

Общему решению однородной системы соответствует собственное возмущенное движение ЛА, а частному - вынужденное. Следовательно, решение уравнений в общем случае можно представить как сумму собственного и вынужденного движений. При исследовании собственного возмущенного движения ЛА выясняется устойчивость опорного движения. Анализ вынужденного движения позволяет определить реакцию ЛА на управляющие воздействия и сделать оценку его управляемости.

В качестве примера решения уравнений классическим методом рассмотрим дифференциальные уравнения с постоянными коэффициентами четвертого порядка, записанные в форме Коши (в скалярной форме), в которой s=1,2,3,4

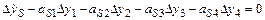. (11.7)

Здесь 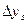- отклонения (вариации) параметров движения, - известные постоянные коэффициенты.

Общее решение получается из суммы произведений частных решений на произвольные постоянные. Поэтому будем сначала искать линейно независимое частное решение (11.7) в виде:

, ( =1,2,3,4) (11.8)

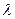Постоянные и определяются так, чтобы при подстановке (11.8) в (11.7) достигалось тождество. Подставляя (11.8) в (11.7) и сокращая на 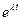получим систему линейных однородных алгебраических уравнений относительно .

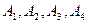(11.9)

Известно, что для получения ненулевых решений таких уравнений определитель системы (11.9) должен быть равен нулю:

(11.10)

Раскрывая определитель (11.10), получим уравнения четвертого порядка для определения 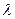, которое называется характеристическим уравнением для системы (11.7):

, (11.11)

где 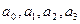- коэффициенты характеристического уравнения, которые выражаются через известные постоянные коэффициенты уравнений (11.7).

При решении характеристического уравнения возможны случаи, когда все корни - различные (простые) или все (или часть) корней будут кратными. Предположим, что все корни уравнения (11.11) действительные и различные. Для каждого корня ( =1,2,3,4) напишем систему уравнений (11.9). Таких систем будет четыре, из которых определим 16 коэффициентов . Причем в каждой системе уравнений один из коэффициентов будет произвольным, который можно принять равным единице (например, =1). Подставляя найденные значения и в (11.8), получим частные решения системы (11.7)

(11.12)

Следовательно, общее решение будет иметь вид:

(11.13)

где определим из начальных условий при t=0,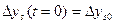

(11.14)

Решение этой системы можно найти, например, по методу Крамера. Из общего решения (11.13) видно, что когда все l_K действительные, то отклонения Dy_s изменяются с течением времени по апериодическому закону и будут возрастать или убывать в зависимости от знаков l_K. Если все l_K будут отрицательными, то при t ®¥ все Dy_s ® 0 и, следовательно, невозмущенное движение будет асимптотически устойчивым, так как все параметры в возмущенном движении будут стремиться к параметрам невозмущенного. Если среди корней l_K найдется хотя бы один положительный, то при t ® ¥ все D y_S будут неограниченно возрастать, и, следовательно, невозмущенное движение будет неустойчивым.

Рассмотрим случай, когда среди корней характеристического уравнения имеются комплексные сопряженные. Пусть два корня окажутся комплексно сопряженными, например l_1,2 = c ± in. Этим корням будет соответствовать частное решение

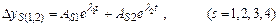
где постоянные A_S1 и A_S2 определяются из решения системы (11.9) и являются комплексными сопряженными числами

A_S1 = a_S - ib_S и A_S2 = a_S + ib_S, тогда

Пользуясь формулами Эйлера , получим

где - новые произвольные постоянные. Откуда видно, что частное движение, соответствующее паре комплексных сопряженных корней, будет колебательным с амплитудой , круговой частотой n и фазой Y_S. Амплитуда будет неограниченно возрастать, если вещественная часть комплексного корня – положительная (c > 0) и затухать, если c < 0. Если два оставшиеся корня l ₃, l ₄ действительные, то собственное возмущенное движение представляет собой наложение одного колебательного и двух апериодических движений, соответствующих корням l ₃, l ₄.

Для решения вопроса об устойчивости или неустойчивости невозмущенного движения можно не определять корни характеристического уравнения, а лишь определить знак вещественной части всех корней, которые для устойчивого дижения должны быть строго отрицательными.

Косвенные признаки, по которым можно судить о знаке вещественной части корней характеристического уравнения линейных систем с постоянными коэффициентами, минуя вычисление самих корней, называются критериями устойчивости. Они подразделяются на алгебраические и частотные.

Алгебраические критерии позволяют судить об устойчивости и неустойчивости систем по коэффициентам характеристического уравнения. Имеются различные формы критериев. Наибольшее применение получили критерии Гурвица и Рауса.

Пусть характеристическое уравнение n -ой степени имеет вид

(11.15)

в котором все коэффициенты a_k – вещественные числа, а a_n > 0. Построим из коэффициентов матрицу Гурвица (n ´ n)

D1		a n-1	a n			·
D2		a n-3	a n-2	a n-1	a n	·
D3		a n-5	a n-4	a n-3	a n-2	·
D4		a n-7	a n-6	a n-5	a n-4	·
·		·	·	·	·	·
Dn							a 0

Теорема Гурвица. Для того, чтобы все корни алгебраического уравнения (11.15) имели отрицательные вещественные части, необходимо и достаточно, чтобы все главные диагональные миноры матрицы Гурвица были положительны.

В частности для уравнения четвёртой степени

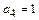() (11.16)

должны выполняться неравенства: ; ;

; .

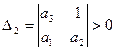Равносильными для уравнения 4-ой степени являются условия Рауса-Гурвица, которые имеют вид: .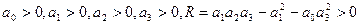

Лекция 17.

Дата добавления: 2015-05-08