К каноническому виду методом ортогональных преобразований

Приведение квадратичной формы

Для любой симметрической матрицы 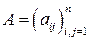(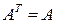) существует ортогональная матрица 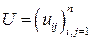() такая, что выполняется равенство

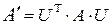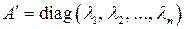, , (10.7)

где 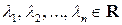– собственные значения матрицы 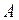, повторяющиеся с учетом их алгебраических кратностей. При этом собственные векторы матрицы 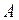, отвечающие различным собственным значениям, ортогональны.

Определение 10.6. Линейное преобразование

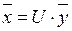(10.8)

с ортогональной матрицей называется ортогональным преобразованием.

В силу того, что всякая ортогональная матрица является неособенной матрица, заключаем, что преобразование (10.8) является невырожденным линейным преобразованием.

Если взять в качестве матрицы 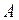матрицу квадратичной формы (10.1), то при помощи ортогонального преобразования (10.8) ее можно привести к виду (10.7). А это означает, что любую квадратичную форму (10.1) с помощьюортогонального преобразования (10.8) можно привести к каноническому виду

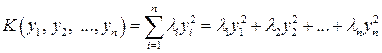. (10.9)

Итак, чтобы найти матрицу , осуществляющую ортогональное преобразование (10.8), необходимо:

1) найти собственные значения 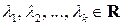(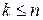) матрицы 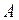, указав соответствующие алгебраические кратности;

2) для каждого собственного значения 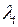(, 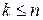) найти соответствующий набор линейно независимых собственных векторов (их количество должно равняться алгебраической кратности собственного числа). В результате получим линейно независимую систему собственных векторов;

3) преобразовать полученную в пункте 2) систему собственных векторов в ортонормированную систему векторов. При этом, если 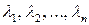– различные собственные значения матрицы 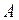, то соответствующая система собственных векторов является ортогональной, и достаточно пронормировать собственные векторы. Если же среди собственных значений 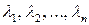есть равные, то необходимо провести процесс ортогонализации Грамма-Шмидта (так как основным пространством является евклидово пространство 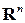, то скалярное произведение задано в нем стандартным образом). В результате получаем ортогональную матрицу , столбцами которой являются векторы ортонормированной системы;

4) записать ортогональное преобразование (10.8) и каноническую форму (10.9).

Пример 10.3. Привести квадратичную форму

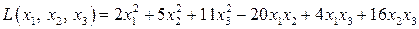
к каноническому виду методом ортогонального преобразования.

Решение. 1) Найдем собственные значения матрицы 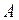квадратичной формы. Матрица 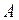квадратичной формы имеет вид

.

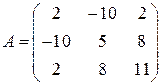Для нахождения собственных значений составляем характеристический многочлен 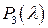матрицы 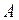квадратичной формы:

.

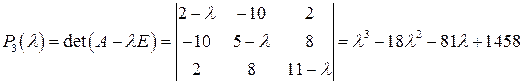Его корни 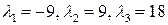– собственные значений матрицы 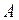квадратичной формы. Так как все собственные значения попарно различны, то алгебраическая кратность каждого собственного значения равна 1.

2) Для каждого собственного значения 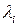(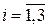) найдем соответствующий собственный вектор

().

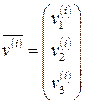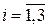Соответствующая однородная система линейных алгебраических уравнений для нахождения собственного вектора 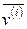(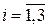) имеет вид

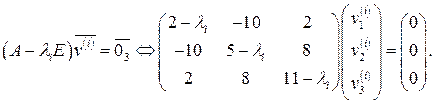(10.10)

Решив для каждого собственного значения 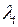(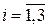) систему (10.10), получим линейно независимую систему собственных векторов

, , ,

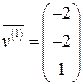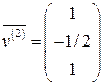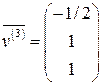соответствующих собственным значениям .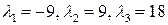

3) Преобразуем полученную в пункте 2) систему собственных векторов в ортонормированную систему векторов. Заметим, что система собственных векторов является ортогональной:

, , .

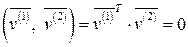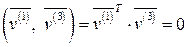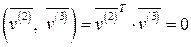Пронормировав собственные векторы 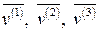, получим систему ортонормированных векторов :

, , ,

, , ,

, , .

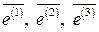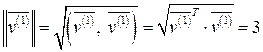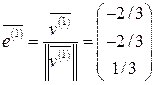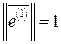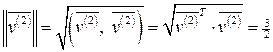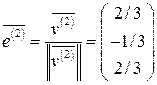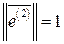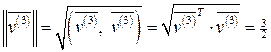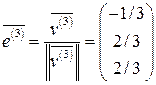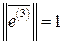В результате получаем ортогональную матрицу преобразования:

,

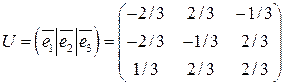столбцами которой являются векторы построенной ортонормированной системы.

4) Соответствующая каноническая форма (10.9) имеет вид

.

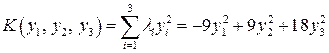Выполним проверку проведенных вычислений. Матрицы исходной квадратичной формы и канонической формы имеют вид

, .

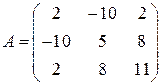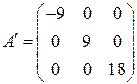Убедимся в справедливости равенства (10.7):

.

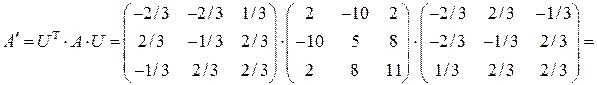
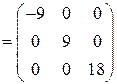Дата добавления: 2015-05-09