Соотношения между БПФ и цифровой фильтрацией 1 страница

Фурье

Спектральный анализ и быстрое преобразование

Набор алгоритмов, называемых алгоритмами быстрого преобразования Фурье (БПФ), включает разнообразные методы уменьшения времени вычисления дискретного преобразования Фурье (ДПФ). Поскольку вычисление ДПФ является основной операцией в большинстве задач спектрального анализа, то использование БПФ, позволяющее многократно ускорить вычисление ДПФ по сравнению с методом прямого вычисления ДПФ, имеет чрезвычайно важное значение и должно рассматриваться как неотъемлимая часть применения методов цифровой обработки сигналов для спектрального анализа.

2.1. Введение в алгоритмы БПФ с основанием 2. Алгоритм БПФ

с прореживанием по времени

Рассмотрим преобразование дискретного сигнала, определенного на N=2i=0,2,4,8,16,... точках. ДПФ конечной последовательности {x(n)}, nÎ[0,N-1] определяется выражением

где kÎ[0,N-1], или в более удобной форме

где

Легко показать, что Wnkявляется периодической последовательностью с периодом N, т. е.

Периодичность Wnkявляется одним из ключевых моментов БПФ. Часто периодичность Wnkподчеркивают тем, что вместо W записывают WN.

Из соотношения (2.1) следует, что в случае, когда последовательность x(n) является комплексной, при прямом вычислении N-точечного ДПФ нужно выполнить (N-1)2комплексных умножений и N(N-1) комплексных сложений. Основная идея БПФ состоит в том, чтобы разбить исходную N-точечную последовательность на две более короткие последовательности, ДПФ которых могут быть скомбинированы таким образом, чтобы получилось ДПФ исходной N-точечной последовательности.

Так, например, если N четное (что всегда имеет место при основании два), а исходная N-точечная последовательность разбита на две (N/2)-точечные последовательности, то для вычисления искомого N-точечного ДПФ потребуется порядка (N/2)2*2=N2/2 комплексных умножений, т. е. вдвое меньше по сравнению с прямым вычислением. Здесь множитель (N/2)2дает число умножений, необходимое для прямого вычисления (N/2)-точечного ДПФ, а множитель 2 соответствует двум ДПФ, которые должны быть вычислены. Эту операцию можно повторить, вычисляя вместо (N/2)-точечного ДПФ два (N/4)-точечных ДПФ и сокращая тем самым объем вычислений еще в два раза. Выигрыш в два раза является приближенным, поскольку не учитывается, каким образом из ДПФ меньшего размера образуется искомое N-точечное ДПФ.

Проиллюстрируем описанную методику для N-точечной последовательности {x(n)}, считая, что N равно степени 2. Введем, как показано на рис. 2.1, две (N/2)-точечные последовательности {x1(n)} и {x2(n)} из четных и нечетных членов x(n) соответственно, т. е.

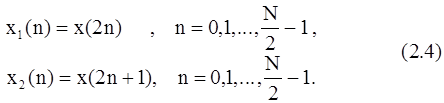
N-точечное ДПФ последовательности {x(n)} можно записать как

С учетом того, что

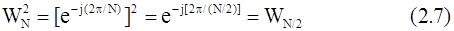перепишем выражение (2.6) в виде

или

где X1(k) и X2(k) - (N/2)-точечные ДПФ последовательностей x1(n) и x2(n) соответственно.

Поскольку X(k) определено при kÎ[0,N-1], а X1(k) и X2(k) определены при kÎ[0,N/2-1], необходимо доопределить формулу (2.9) для k³N/2. Принимая во внимание свойство периодичности ДПФ, можем записать

.

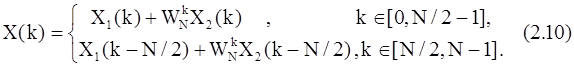
Заметим также, что

Рис. 2.1

поэтому формулу (2.10) можно переписать в виде

На рис. 2.2 с помощью направленного графа представлена последовательность операций при выполнении восьмиточечного ДПФ с использованием двух четырехточечных преобразований. Входная последовательность x(n) сначала разбивается на две последовательности x1(n) и x2(n) из четных и нечетных членов x(n), после чего вычисляются их преобразования X1(k) и X2(k). Затем в соответствии с (2.10*) получают X(k).

Рассмотренная схема вычислений может быть использована для расчета (N/2)-точечных ДПФ в соответствии с формулами (2.9) и (2.10). Каждая из последовательностей x1(n) и x2(n) разбивается на две последовательности, состоящие из четных и нечетных членов. Аналогично (N/2)-точечные ДПФ могут быть записаны как комбинации двух (N/4)-точечных ДПФ, т. е.

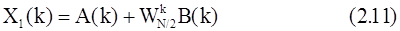
Рис. 2.2

или

где kÎ[0,N/2-1], A(k) и B(k) - N/2-точечные ДПФ соответственно четных и нечетных членов x1(n). На рис. 2.3 показан результирующий направленный граф, в котором четырехточечные ДПФ из рис. 2.2 рассчитываются согласно (2.12).

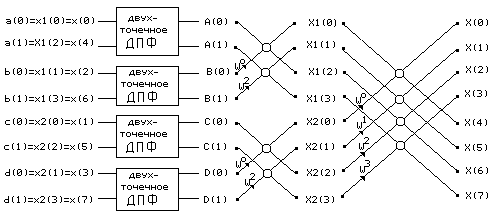Рис. 2.3

Процесс уменьшения размера ДПФ от L до L/2, где L равно степени 2, может быть продолжен до тех пор, пока не останутся только двухточечные ДПФ. Двухточечное ДПФ F(k), k=0,1 может быть рассчитано без использования умножений по формулам

Здесь f(n), n=0,1 - преобразуемая двухточечная последовательность. Поскольку W08=1 и W48=-1, для вычислений по формулам (2.13) действительно не нужны операции умножения. Таким образом, восьмиточечное ДПФ (рис. 2.1 и рис. 2.3) в итоге сводится к алгоритму, описываемому направленным графом, представленным на рис. 2.4.

2.1.1. Некоторые свойства алгоритма БПФ с основанием 2

и прореживанием по времени

Анализ графа на рис. 2.4 и процедуры последовательного сокращения вдвое размера преобразований показывает, что на каждом этапе БПФ (т. е. при каждом сокращении размера ДПФ) необходимо выполнить N/2 комплексных умножений. Поскольку общее количество этапов равно log2N, то число комплексных умножений, необходимое для нахождения N-точечного ДПФ, приблизительно равно (N/2)log2N. Слово приблизительно использовано по той причине, что умножения на W0N, WN/2N, WN/4Nи W3N/4Nв действительности сводятся просто к сложениям и

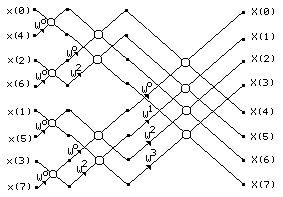Рис. 2.4

вычитаниям комплексных чисел. Как следует из направленного графа на рис. 2.4, вместо ожидаемых 12 (т. е. 4log28) достаточно выполнить всего два нетривиальных умножения. Однако для большинства значений N фактическое число нетривиальных умножений хорошо аппроксимируется выражением (N/2)log2N.

Базовая операция алгоритма с прореживанием по времени (так называемая "бабочка") состоит в том, что два входных числа А и В объединяются для получения двух выходных чисел X и Y следующим образом:

На рис. 2.5 изображен направленный граф базовой операции.

Рис. 2.5

Внимательное рассмотрение графа на рис. 2.4 показывает, что каждый из этапов содержит N/2 базовых операций. В случае, когда множитель WkN- нетривиальный, для каждой базовой операции необходимо выполнить только одно умножение, поскольку величину BWkNможно вычислить и запомнить. Таким образом, структура базовых операций такова, что для выполнения БПФ N-точечной последовательности, размещенной в памяти, достаточно иметь лишь одну дополнительную ячейку памяти. Результаты всех промежуточных этапов БПФ можно размещать в те же ячейки памяти, где находятся исходные данные. Поэтому для хранения и входной и выходной последовательностей можно использовать один и тот же массив ячеек памяти. Алгоритм, в котором для размещения входной и выходной последовательностей используются одни и те же ячейки памяти, называется алгоритмом БПФ с замещением.

2.2. Перестановка данных и двоичная инверсия

Еще одной особенностью алгоритма с прореживанием по времени (как, впрочем, и большинства других алгоритмов БПФ) является необходимость такой перестановки элементов входной последовательности, чтобы выходная последовательность X(k) имела естественный (прямой) порядок расположения, т.е. k=0,1,..., N-1. В примере на рис. 2.4 для этого требовался следующий порядок размещения входной последовательности: x(0), x(4), x(2), x(6), x(1), x(5), X(3), x(7). Характер перестановки элементов входной последовательности может быть описан сравнительно просто. В случае, когда N является степенью 2, входная последовательность должна быть расположена в памяти в двоично-инверсном порядке для того, чтобы выходная последовательность получилась в прямом порядке. Двоично-инверсный порядок определяется следующим образом. Если записать порядковые номера элементов входной последовательности в двоичном коде, используя L двоичных разрядов, причем N=2L, а затем инвертировать порядок следования разрядов, то получаемые при этом числа и будут номерами элементов входной последовательности после их перестановки. Так, для случая N=8=23прямой порядок номеров приведен в таблице 2.1 слева, а двоично-инверсный - справа. Таким образом, для двоичной инверсии входной последовательности необходим соответствующий алгоритм.

Перестановку входной последовательности можно произвести с замещением, меняя в парах местами числа с прямыми и двоично-инверсными номерами и используя для этого лишь одну вспомогательную ячейку памяти.

Таблица 2.1

Номер	Двоичное представление	Двоичная инверсия	Двоично-инверсный номер

Перестановку входной последовательности можно произвести с замещением, меняя в парах местами числа с прямыми и двоично-инверсными номерами и используя для этого лишь одну вспомогательную ячейку памяти.

Рис. 2.6

На рис. 2.6 показана схема перестановки данных, представленных в табл. 2.1.

Отметим еще одну особенность алгоритма БПФ, заключающуюся в том, что на всех этапах преобразования используются коэффициенты WkN, k=0, 1,..., N-1. Существует несколько способов получения этих коэффициентов. Простейший способ - составление таблицы, к которой можно обращаться в процессе счета. Единственный недостаток этого способа заключается в том, что для хранения этих коэффициентов необходима дополнительная память примерно из N ячеек.

Второй способ заключается в непосредственном вычислении коэффициентов WkN=cos[(2p/N)k]-jsin[(2p/N)k] с использованием каждый раз стандартных подпрограмм расчета синуса и косинуса. Этот способ связан с большими затратами времени, поскольку вычисление этих функций, как правило, достаточно продолжительно.

Третий способ основан на применении простой рекуррентной формулы

с начальным условием W0N=1, т. к. степени W на каждом этапе БПФ меняются с постоянным шагом. Так, в примере на рис. 2.4 на первом этапе используются коэффициенты W0 и W4, на втором - W0, W2, W4, W6, а на третьем - Wk, k=0, 1, 2,..., 7. Поэтому, чтобы иметь возможность на каждом из этапов использовать формулу (2.14), достаточно запомнить или вычислить только множители W4, W2 и W0.

2.3. Алгоритм БПФ с прореживанием по частоте

Другая распространенная форма алгоритма БПФ (при условии, что N равно степени 2) - так называемый алгоритм БПФ с прореживанием по частоте. В этом варианте алгоритма БПФ последовательность {x(n)} разбивается на две последовательности, содержащие по N/2 отсчетов каждая, следующим образом: первая последовательность {x1(n)} состоит из первых (N/2) отсчетов {x(n)}, а вторая {x2(n)} - из остальных (N/2) отсчетов {x(n)}, т. е.

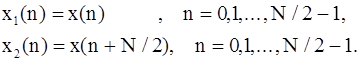
При таком разбиении N-точечное ДПФ последовательности x(n) можно записать в виде

Учитывая, что

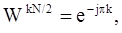получим

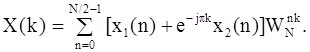
Запишем выражения отдельно для четных и нечетных отсчетов ДПФ

Из данных выражений видно, что четные и нечетные отсчеты ДПФ можно получить из (N/2)-точечных ДПФ последовательностей f(n) и g(n), равных

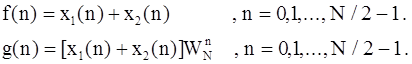
Таким образом, снова вычисление N-точечного ДПФ удалось свести к вычислению двух (N/2)-точечных ДПФ. На рис. 2.7 эта методика иллюстрируется для случая N=8.

Рис. 2.7

Описанную методику можно применить повторно и представить каждое из (N/2)-точечных ДПФ в виде комбинаций двух (N/4)-точечных ДПФ. На рис. 2.8 и рис. 2.9 показан переход от четырехточечных ДПФ (рис. 2.7) к двухточечным ДПФ с последующим прямым вычислением двухточечных ДПФ.

Рис. 2.8

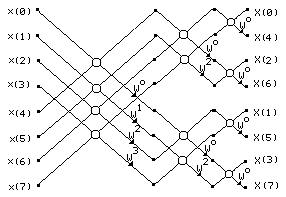Рис. 2.9

Рис. 2.10

Сравнение алгоритмов, иллюстрированных на рис. 2.4 и 2.9, позволяет выявить два очевидных различия между ними. Во-первых, при прореживании по времени порядок следования входных отсчетов двоично-инверсный, а выходных - прямой и наоборот при прореживании по частоте (рис. 2.9). Однако это отличие кажущееся, поскольку в обоих алгоритмах порядок следования входных отсчетов может быть прямым, а выходных - двоично-инверсным и наоборот. Второе отличие заключается в несколько ином выполнении базовой операции (см. рис. 2.5 и 2.10): при прореживании по частоте комплексное умножение выполняется после сложения (вычитания).

Легко заметить и сходство между алгоритмами с прореживанием по времени и по частоте. В обоих случаях при вычислении БПФ требуется около Nlog2N операций, вычисления могут быть проведены с замещением и должно быть предусмотрено выполнение двоичной инверсии.

2.4. Вычисление обратного ДПФ с помощью алгоритма прямого ДПФ

Для вычисления обратного ДПФ можно без каких-либо изменений использовать алгоритм БПФ. Обратное ДПФ N-точечной последовательности {X(k)}, k=0,1,..., N-1, определяется следующим образом:

Взяв выражение, комплексно-сопряженное с (2.15), и умножив его на N, получим

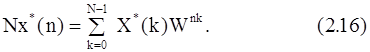
Правая часть формулы (2.16) представляет собой ДПФ последовательности {X*(k)} и может быть вычислена с использованием одного из описанных алгоритмов БПФ. Искомую последовательность {x(n)} можно получить, взяв комплексно-сопряженное с (2.16) выражение и разделив его на N, т. е.

Таким образом, алгоритм БПФ обеспечивает вычисление и прямого и обратного ДПФ.

2.5. Единый подход к алгоритмам БПФ

Существует много различных алгоритмов БПФ. Однако, оказывается, что все они могут быть получены с помощью последовательного применения единственной операции, а именно представления одномерного массива чисел двумерным.

При вычислении N-точечного ДПФ N-точечной последовательности целое N может быть либо простым, либо составным числом (до сих пор считалось, что N состоит из большого числа сомножителей и равно степени 2). Если N простое, его нельзя разложить на произведения меньших целых чисел. В этом случае одномерный сигнал x(0), x(1),..., x(N-1) невозможно представить в виде двумерного массива, поэтому для такого сигнала не существует алгоритма БПФ.

В большинстве практических задач вполне допустимо искусственное удлиннение обрабатываемой последовательности путем добавления нулей, приводящее к тому, что результирующий спектр представляет собой некоторую интерполяцию спектра неудлинненной последовательности. Пусть, например, N равно 60. Это число можно представить как произведение меньших чисел различным образом: 60=3*4*5=4*3*5=5*4*3=12*5=2*2*3*5 и т. д. В зависимости от порядка следования сомножителей и их общего количества могут быть получены различные формы алгоритма БПФ. Для характеристики разложения обычно используют понятие "основание". Понятие "смешанное основание" означает, что не все сомножители N одинаковы. Для N=60 все формы алгоритма БПФ имеют смешанные основания. Если N можно представить в виде произведения одинаковых сомножителей r, то соответствующий алгоритм называют алгоритмом БПФ с основанием r. Например, если N=64=2*2*2*2*2*2, то получаются рассмотренные ранее алгоритмы БПФ с основанием 2. Если же N записать как 64=8*8, то получится алгоритм БПФ с основанием 8.

Очень важно отметить, что разложение числа на множители можно выполнить различными способами. Следовательно, для выявления общих закономерностей следует провести тщательный анализ свойств разложения очередного числа на два сомножителя. Возьмем в качестве примера снова N=60 и запишем одно из возможных разложений обрабатываемого массива в виде матрицы из (5*12) номеров отсчетов сигнала:

Далее, поскольку столбцы содержат по пять (т. е. простое число) отсчетов, они больше не могут быть разложены. Однако строки, состоящие из 12 отсчетов, можно представить в виде матриц размером (3X4). Например, первая строка будет иметь вид:

Остальные строки можно представить аналогично. Итак, теперь нужно установить, каким образом, оперируя с двумерным массивом, можно получить ДПФ исходного одномерного массива.

Для получения основного результата будем считать, что входные отсчеты пронумерованы по строкам и столбцам, поэтому их номера могут быть представлены следующими парами чисел:

0,0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	0,10	0,11
1,0	1,1	1,2	1,3	1,4	1,5	1,6	1,7	1,8	1,9	1,10	1,11
2,0	2,1	2,2	2,3	2,4	2,5	2,6	2,7	2,8	2,9	2,10	2,11
3,0	3,1	3,2	3,3	3,4	3,5	3,6	3,7	3,8	3,9	3,10	3,11
4,0	4,1	4,2	4,3	4,4	4,5	4,6	4,7	4,8	4,9	4,10	4,11

Далее, пусть текущий номер столбца равен m (m=0, 1,...,11), а l (l=0, 1,..., 4) - текущий номер строки. Если исходный номер отсчета обозначить через n (n=0, 1,..., 59), то

n=Ml+m, (2.17)

где M - число столбцов, а L- число строк (в данном примере M=12, L=5).

Допустим, что мы можем найти ДПФ двумерного массива с двойными номерами, тогда результат должен иметь вид двумерного масива с двойными номерами. Пусть m и l - переменные исходного сигнала, а r и s - переменные двумерного ДПФ по столбцам и строкам соответственно, которые преобразуются в одну переменную следующим образом

k=Lr+s. (2.18)

Теперь коэффициенты одномерного ДПФ X(k)=X(s,r) можно выразить через преобразование массива x(n)=x(l,m), используя простую подстановку формул (2.17) и (2.18) в выражение для ДПФ (2.2), что дает

Разлагая

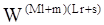с учетом того, что

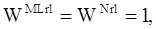
и располагая соответствующие переменные под знаком суммирования, преобразуем формулу (2.19) к следующему виду

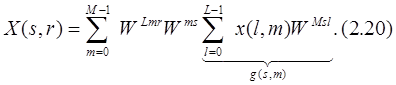
Эта формула содержит все необходимые сведения, позволяющие связать преобразование одномерного массива с преобразованием того же массива, представленного в виде двумерной матрицы.

Заметим прежде всего, что внутренняя сумма представляет собой ДПФ m-го столбца исходного массива с ядром преобразования WM. Таким образом, можно сформулировать первый шаг последовательности расчета X(k):

1. Вычислить L-точечные ДПФ всех столбцов. Результат является функцией s и m, причем m меняется от 0 до M-1. Обозначим его через g(s,m) и перепишем формулу (2.20):

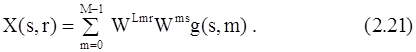
Отсюда следует, что второй шаг вычисления X(k) сводится к следующему.

2. Найти новый массив h(s,m), умножая каждый элемент g(s,m) на поворачивающий множитель Wms.

Теперь формула (2.21) примет вид

Она представляет M-точечное ДПФ каждой из строк с номерами s. Поэтому последний шаг алгоритма заключается в следующем.

3. Вычислить M-точечные ДПФ всех строк матрицы h(s,m) с ядром преобразования WL.

Описанная методика напоминает вычисление двумерного ДПФ, когда сначала вычисляются ДПФ строк, а затем столбцов, но шаг 2 отсутствует. Разделимость ядра преобразования с более высокой размерностью и является причиной того, что при расчете ДПФ с более высокой размерностью требуется меньше операций, чем при расчете одномерного ДПФ при одинаковом общем числе отсчетов.

Важно отметить, что после введения поворачивающих множителей, т.е. после второго шага описанной выше методики, способы расчета двумерного ДПФ и одномерного ДПФ массива, представленного в виде двумерной матрицы, становятся эквивалентными, причем при каждом таком представлении для выполнения шага 2 требуется дополнительно до N умножений. Изменение порядка суммирования в формуле (2.19) дает

Так что порядок вычисления X(k) становится следующим:

1. Умножить отсчеты сигнала x(l,m) на поворачивающие множители Wms.

2. Вычислить M-точечные ДПФ всех строк.

3. Вычислить L-точечные ДПФ всех столбцов.

В этом случае умножение на поворачивающие множители предшествует вычислению ДПФ строк, тогда как раньше они выполнялись после вычисления ДПФ столбцов. Эти отличия от рассмотренного ранее порядка вычисления X(k) не только напоминают, но и действительно связаны с обсуждавшимся выше различием между алгоритмами ДПФ с основанием 2 при прореживании по времени и по частоте.

Отметим еще одно важное свойство методики преобразования, вытекающее из формулы (2.19), в которой переменные m и r являются номерами столбцов, а l и s - номерами строк. При увеличении m на единицу номер отсчета исходного массива (Ml+m) также возрастает на единицу, тогда как при увеличении на единицу номера столбца преобразованного массива r аргумент X(s,r) возрастает на L. Это означает, что в результате преобразования номера строк и столбцов меняются местами.

2.6. Особенности цифровой реализации алгоритма БПФ

Вычисление быстрого преобразования Фурье является одним из ключевых моментов спектрального анализа, поэтому эффектам конечной разрядности данного алгоритма должно быть уделено особое внимание. К таким эффектам относятся шумы округления при усечении результатов умножений, погрешности масштабирования промежуточных результатов с целью устранения возможных переполнений, а также погрешности представления коэффициентов Wk(поворотных множителей). Уэлч и ряд других авторов [2] подробно проанализировали влияние шума округления и масштабирования для алгоритмов БПФ по основанию 2 с прореживанием по времени и по частоте при условии, что все арифметические операции выполняются с фиксированной запятой. Вопрос, связанный с точностью представления коэффициентов, не рассматривался столь подробно, поэтому будут приведены лишь качественные результаты.

Рассмотрим реализацию алгортма БПФ с основанием 2 при выполнении арифметических операций с фиксированной запятой.

Если последовательность {x(n)} из N отсчетов имеет коэффициенты ДПФ {X(k)}, то, согласно теореме Парсеваля,

т. е. средняя мощность выходных гармоник в N раз превышает среднюю мощность исходной последовательности. Следовательно, значения ДПФ последовательности будут, вообще говоря, существенно превышать значения самой последовательности. При теоретическом рассмотрении этот факт не играет особой роли, но как только дело доходит до практической реализации на устройстве, имеющем целочисленную арифметику, то тут уже приходится заботиться о том, чтобы числа не выходили за пределы разрядной сетки, т. е. чтобы не было переполнения. Проиллюстрируем возникновение переполнений на примере базовой операции ("бабочки") на m-ом этапе БПФ с прореживанием по времени:

Дата добавления: 2015-05-09