Модель линейной регрессии

До сих пор рассматривались статистические выводы для моделей, соответствующих повторным независимым наблюдениям над некоторой случайной неличной 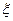. В этих случаях исходные статистические данные представляют собой реализацию случай­ного вектора 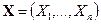, компоненты которого независимы и одинаково распределены, а именно 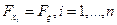. В при­ложениях математической статистики предположения о незави­симости и одинаковой распределенности компонент 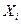не всегда выполняются. В этой главе будет рассмотрен важный случай таких ситуаций, часто встречающихся в приложениях, которые описываются в терминах линейной регрессионной модели. В этой модели предполагается, что математические ожидания наблюде­ний 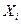являются линейными функциями 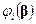от неизвестных параметров и делаются некоторые предположения о вторых моментах.

В общем случае речь идет об изучении таких случайных экспериментов, когда на их исход влияют некоторые неслучайные переменные (факторы) 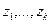, значения которых меняются от опыта к опыту. Например, 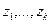могут быть входными характеристиками прибора, при каждой задаваемой произвольно комбинации значений которых наблюдается некоторый эффект («отклик») как исход эксперимента. В других случаях значения факторов для каждого опыта могут быть обусловлены не

зависящими от исследователя причинами (как правило, это имеет место, например, в экономических исследованиях). Но в любом случае статистические данные состоят из множества наблюдав­шихся значений «откликов» 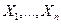и соответствующих значений факторов, т.е. имеют вид 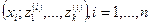; при этом всегда предполагается, что .

Часто можно считать, что факторы 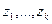оказывают влияние только на среднее значение «отклика», при этом математическое ожидание исхода 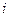-го опыта имеет вид

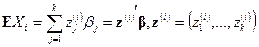
т.е. является линейной функцией неизвестных параметров 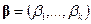. (Напомним, что при матричных преобразованиях векторы всегда понимаются как вектор-столбцы.) Другими сло­вами, случайную величину 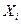, описывающую результат 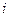-го опыта, можно представить в виде

,

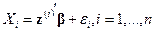где 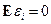и распределение «ошибок» 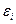от параметров 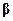не зависит. Введем матрицу плана 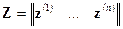размером 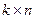, составленную из вектор-столбцов 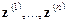, и вектор ошибок 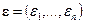. Тогда в матричных обозначениях предыдущие равенства принимают вид

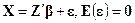. (5.1)

Далее обычно предполагают, что случайные величины 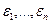(или, что то же самое, 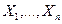) не коррелированы и имеют одинаковые дисперсии 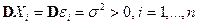, где 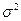обычно неизвестно. В этом случае матрица вторых моментов вектора наблюдений 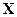имеет следующий вид:

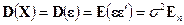. (5.2)

Если выполняются условия (5.1) — (5.2), то говорят, что имеет место модель линейной регрессии. Параметры 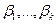называют коэффициентами регрессии, а 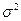— остаточной дисперсией.

В описанной схеме переменные 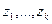могут быть функ­ционально зависимы. В частности, все 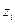могут являться функ­циями одной переменной 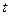, например 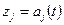, где 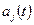— полином степени 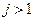, в этом случае говорят о параболической регрессии.

В более общем случае возможны корреляции между наблюде­ниями, т.е. вместо условия (5.2) вводится условие .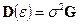

Если матрица 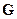известна, то, положив 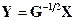, получим, что преобразованные таким образом данные удовлетворяют

модели (5.1) — (5.2) (при линейном преобразовании 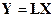первые и вторые моменты случайного вектора преобразуются следующим образом: 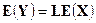, 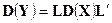). Таким образом, подробного изучения заслуживает только стандартная модель (5.1)-(5.2).

Далее определяющую роль играет матрица

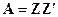(5.3)

Эта матрица всегда неотрицательно определена и положительно определена тогда и только тогда, когда 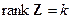, т. е. когда строки матрицы 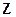линейно независимы. Действительно, квадратичная форма 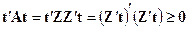, 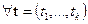причем равенство нулю возможно только при 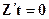. В свою очередь, это равенство эквивалентно равенству 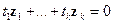; где 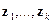— столбцы матрицы 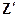. Таким образом, равенстве нулю 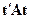при некотором 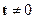имеет место только в случае линейной зависимости векторов 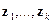, т. е. при .

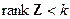Излагаемая далее теория строится в предположении, что матрица 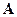не вырождена (или, что эквивалентно, 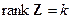). Полные результаты, относящиеся и к вырожденному случаю, можно найти в [28. гл. 4].

Дата добавления: 2015-05-09