Преобразователи кодов

В цифровой измерительной аппаратуре важное место занимают преобразователи кодов. По определению и по сути преобразователем кодов является любое КЦУ, поскольку как и КЦУ, преобразователь кодов преобразует n -разрядный входной код в m -разрядный выходной. Частным случаем преобразователей кодов можно рассматривать шифраторы и дешифраторы, выполняющие преобразование десятичного кода в двоичный и обратно. Однако существует класс устройств, традиционно относящихся по своим функциональным свойствам к категории преобразователей кодов. Распространенность использования преобразоветелей кодов можно объяснить тем, что они позволяют аппаратно реализовывать функции преобразования кодов с устройств ввода-вывода, т.е. с максимальным быстродействием. Использование преобразователей кодов часто можно встретить даже в измерительной и управляющей аппаратуре на базе микропроцессорной и микроконтроллерной техники. Несмотря на усложнение при этом электрической схемы устройства, повышение быстродействия и получение более простой управляющей программы делает использование преобразователей кодов оправданным.

В общем случае функция преобразования кодов задается в функциональном поле УГО элемента обозначением «X / Y», где X – входный код, а Y – выходной. В каждом конкретном случае, если это возможно, желательно вместо X и Y указывать конкретные обозначения, например, «2/2-10» для преобразователя двоичного кода в двоично-десятичный.

Часто требуется вводить информацию в цифровую систему с привычных для человека десятичных устройств, например с кнопочных клавиатур из десяти кнопок. Задача такого преобразования легко решается с помощью шифраторов. Пример организации подобного решения был рассмотрен ранее. Но, поскольку обработка информации в цифровом устройстве реализуется обычно по правилам двоичной арифметики и результат представлятся в двоичном коде, то для вывода результата на десятичные устройства, например, на десятичные индикаторы, система вывода инфорации должна быть снабжена двоично-десятичным преобразователем. Преобразователи двоично-десятичных кодов выполняют преобразование чисел, представленных в двоичной системе счисления, в двоично-десятичные числа и обратно в соответствии с таблицей 8.12 на примере преобразования их десятичных эквивалентов в диапазоне значений от 0 до 63.

Таблица 8.12

Десят. число

Двоичные входы

Двоично-десятичные выходы

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

Для реализации данной функции можно воспользоваться обычным методом синтеза КЦУ на базе логических элементов. При этом получится достаточно сложная и громоздкая система ФАЛ со слабо выраженной минимизацией, требующая для своей реализации значительных аппаратных затрат. Поэтому промышленностью выпускаются микросхемы масочных ПЗУ для преобразователей двоично-десятичных кодов, в которых функция преобразования реализуется путем программирования в микросхему таблицы истинности как карты памяти ПЗУ. Данный подход является часто используемым при реализации многих КЦУ. При таком подходе наборы входных переменных рассматриваются как адресные входы микросхемы ПЗУ, а выходные переменные как ее выходные данные. Тогда таблица истинности КЦУ рассматривается как таблица «прошивки» ПЗУ. Данный метод построения КЦУ на базе микросхем ПЗУ позволяет реализовывать сложные нестандартные преобразователи путем простого программирования микросхем ПЗУ, сокращая тем самым время на разработку и удешевляя ее. Примером таких преобразователей могут служить микросхемы К155ПР6 и К155ПР7 (рис. 8.30). Первая является преобразователем двоично-десятичного кода в двоичный, а вторая – двоичного кода в двоично-десятичный. Микросхемы являются постоянными запоминающими устройствами, программирование которых произведено на заводе-изготовителе.

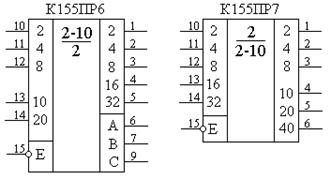
Рис. 8.30. УГО микросхем преобразователей двоично-десятичных кодов К155ПР6 и К155ПР7.

Поскольку младший разряд двоично-десятичного и двоичного кодов соответствующих десятичных эквивалентов совпадают, то младший разряд передается мимо микросхем ПР6 и ПР7. Преобразование начинается со второго разряда. Одна микросхема К155ПР6 позволяет преобразовать двоично-десятичный код чисел от 0 до 39 (входы 2, 4, 8, 10, 20) в двоичный (выходы 2, 4, 8, 16, 32), а одна микросхема К155ПР7 – двоичный код чисел от 0 до 63 (входы 2, 4, 8, 16, 32) в двоично-десятичный (выходы 2, 4, 8, 10, 20, 40).

Микросхема К155ПР6 позволяет также преобразовать двоично-десятичный код чисел от 0 до 9 в код дополнения до 9 (рис. 8.31, а) и до 10 (рис. 8.31, б). В качестве выходов кода дополнения используются выводы A, B и C микросхемы, а в качестве входов двоично-десятичного кода используются выводы 2, 4, 8, 16. Сумма десятичных чисел, соответствующих входному и выходному кодам схемы рис. 8.31, а, равна 9 (например, числу 6 дополнением до 9 является число 3), а схемы рис. 8.31, б – 10. Использование кодов дополнения позволяет осуществлять проверку правильности передачи данных по каналам связи (интерфейсам). В процессе пересылки данных на передающей стороне осуществляется передача вначале самого кода числа, а затем кода его дополнения до некоторого значения (в нашем случае до 9 или до 10). На принимающей стороне осуществляется прием кодов как самого числа, так и его дополнения. Далее оба этих кода суммируются сумматором и проверяется, получилась ли сумма равной значению числа, дополнение до которого осуществлялось на передающей стороне. Если полученная сумма равна значению этого числа, то передача данных прошла без ошибок. Если же сумма отличается от значения этого числа, то в процессе передачи произошел сбой и передачу необходимо повторить.

Рис. 8.31. Преобразователи двоично-десятичного кода в код дополнения до 9 (а) и 10 (б).

Для увеличения разрядности преобразователей кодов на базе микросхем К155ПР6 и К155ПР7 используется каскадное включение этих микросхем. На рис. 8.32, а показан пример преобразователя двоично-десятичного кода чисел от 0 до 99 в двоичный, а на рис. 8.32, б – пример преобразователя двоичного кода чисел от 0 до 255 в двоично-десятичный. Возможно и дальнейшее наращивание разрядности путем каскадного соединения данных микросхем. Однако для реализации двоично-десятичных преобразователей на больший диапазон чисел целесообразнее выполнить программирование прожигаемой ПЗУ согласно таблицы соответствия двоичных и двоично-десятичных чисел необходимой разрядности.

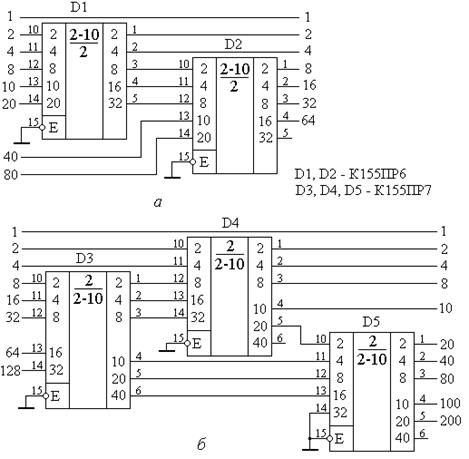
Рис. 8.32. Преобразователь двоично-десятичного кода чисел от 0 до 99 в двоичный (а) и двоичного кода чисел от 0 до 255 в двоично-десятичный (б).

Для отображения результата цифровое измерительное устройство может оснащаться цифровым индикатором. Чаще всего в цифровых схемах, построенных по принципу «жесткой логики», в качестве индикаторов используются семисегментные индикаторы, рассмотренные в разделе 1.12. Поскольку выходной код с цифрового устройства в большинстве случаев формируется двоичным или двоично-десятичным после соответствующего преобразователя, его необходимо преобразовать к входному коду семисегментного индикатора. Такое преобразование реализуется семисегментным преобразователем. Логика его работы задается таблицей 8.13 (для конкретности определим, что свечение сегментов индикатора осуществляется логической единицей).

Таблица 8.13.

Индицируемая десятичная цифра	Входы	Выходы
X 3	X 2	X 1	X 0	a	b	c	d	e	f	g

Можно найти систему ФАЛ, заданных таблицей истинности, минимизировать ее и реализовать структуру преобразователя в выбранном базисе логических элементов в соответствии с рассмотренными выше способами. Существуют уже готовые выпускаемые промышленностью интегральные схемы преобразователей двоично-десятичных кодов в семисегментные. Есть также преобразователи, реализующие преобразование двоичных четырехразрядных кодов в семисегментные. Для таких преобразователей будут определены не только десять наборов входных переменных с номерами от 0 до 9, а все шестнадцать. Обычно для оставшихся шести наборов с номерами от 10 до 15 для таких преобразователей соответствуют семисегментные коды, высвечивающие символы «A», «b», «c», «d», «E» и «F» шестнадцатеричной системы счисления.

В качестве примера блока индикации одноразрядной десятичной цифры рассмотрим пример использования микросхем КР514ИД1 и КР514ИД2. Обе эти микросхемы представляют преобразователь двоичного четырехразрядного кода (входы 1, 2, 4, 8) в семисегментный. Микросхема КР514ИД1 предназначена для использования с индикаторами с разъединенными анодами (рис. 8.33, а), а микросхема КР514ИД2 – с индикаторами с разъединенными катодами (рис. 8.33, б). Выходы микросхемы КР514ИД2 выполнены с открытыми коллекторами. Обе микросхемы снабжены прямым входом разрешения Е. Работа микросхем разрешается при подаче логической единицы на этот вход. При подаче на этот вход уровня напряжения логического нуля независимо от двоичного кода на входах 1, 2, 4, 8 все сегменты индикатора гасятся. Микросхемы обеспечивают индикацию десяти цифр от «0» до «9» и пяти нестандартных символов. При подаче на входы 1, 2, 4, 8 уровней логических единиц индикация отсутствует. Использование резисторов R 1 - R 7 совместно с микросхемой КР514ИД2 необходимо для ограничения тока через сегменты индикатора и коллекторы выходных транзисторов микросхемы. Их номинал рассчитывается из допустимого тока свечения I _св сегментов индикатора, напряжения U _св на этих сегментах в режиме свечения и напряжения питания + U_п, подаваемого на объединенные аноды индикатора:

.

Рис. 8.33. Схемы одноразрядных индикаторов десятичных цифр на микросхемах КР514ИД1 (а) и КР514ИД2 (б).

Существуют микросхемы преобразователей кодов и для индикаторов с другим количеством и другой геометрией сегментов. Такие индикаторы и преобразователи кодов обладают большей функциональностью и позволяют отображать не только цифры, но и символы латиницы и кириллицы. Например, существуют индикаторы, расположение сегментов в которых позволяет высвечивать символ «Ж» и другие сложные символы. Также существуют преобразователи кодов для матричных индикаторов, о которых рассказывалось в разделе 1.12. Такие индикаторы обладают еще большей функциональностью по сравнению с сегментными индикаторами, поскольку позволяют отображать практически любые символы. Поскольку логика управления подобными индикаторами сложна, преобразователи кодов для них часто выполняют на основе микросхем ПЗУ. Подобные преобразователи настроены на определенную кодировку символьной информации (чаще кодировка ASCII) и обеспечивают управление индикатором для высвечивания определенного символа по подаваемому на них коду этого символа. Подобные преобразователи часто имеют свободное адресное пространство пользователя для возможности программирования в них кодовой страницы спецсимволов, например, символов национальных алфавитов.

При необходимости индикации десятичных цифр большой разрядности можно на каждый индикатор отдельного разряда десятичного числа устанавливать отдельные семисегментные преобразователи и подавать на их входы одновременно соответствующие двоично-десятичные коды. Это вызовет одновременную индикацию всех разрядов десятичного числа. Недостаток такой организации заключается в значительном повышении потребления тока от источника питания, что особенно существенно при питании устройства от автономных источников питания, а также в необходимости большого количества электрических связей. Данного недостатка лишены устройства индикации с динамическим управлением, о котором упоминалось в разделе 1.12. Принцип динамической индикации заключается в том, что в определенный момент времени осуществляется индикация только одного разряда индикатора или определенной группы разрядов (знакомест, сегментов) в случае сложных индикаторов. Остальные разряды в это время находятся в погашенном состоянии. Обеспечивая чередование индицируемых разрядов с определенной частотой (сотни Герц и выше), можно добиться восприятия человеческим зрением равномерности и постоянства свечения всех разрядов индицируемого числа. Пример структуры устройства динамической индикации на основе полупроводниковых семисегментных индикаторов с разъединенными катодами для индикации восьмиразрядного десятичного числа приведен на рис. 8.34.

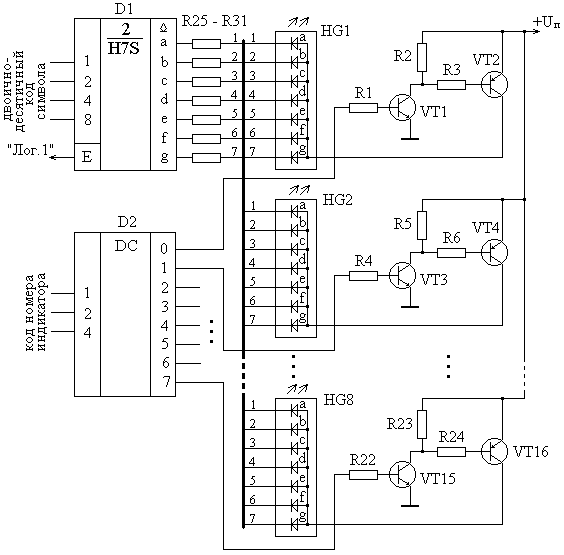
Рис. 8.34. Схема динамической индикации восьмиразрядного десятичного числа.

Формирование семисегментных кодов для всех восьми индикаторов осуществляется только одним преобразователем D 1. Каждый индикатор снабжен схемой электронного ключа на двух транзисторах VT 1 и VT 2 (VT 3 – VT 16) и трех резисторах R 1, R 2 и R 3 (R 4 – R 24), который подключает его объединенные аноды к источнику питания, тем самым задавая ток в сегментах этого индикатора и обеспечивая его свечение. Управление ключами и, таким образом, подключением индикаторов к + U_п осуществляется с помощью дешифратора выбора номера индикатора D 2. Наличие логической единицы на выходе «0» дешифратора вызывает насыщение и открытие транзистора VT 1, на коллекторе которого формируется нулевой потенциал общего провода. Это в свою очередь вызывает насыщение и открытие транзистора VT 2, который подключает индикатор HG 1 к источнику питания. На остальных выходах дешифратора в этот момент присутствуют логические нули, в результате которых транзисторы VT 3 – VT 16 находятся в режиме отсечки и, следовательно, закрыты. Для включения второго индикатора необходимо, чтобы на выходе «1» дешифратора сформировалась логическая единица. При этом на остальных выходах дешифратора будут присутствовать потенциалы логических нулей, что приведет к закрытию соответствующих ключей и отключению соответствующих индикаторов от источника питания. Таким образом, обеспечивается подключение только одного из восьми индикаторов в определенный момент времени. Выбор подключаемого индикатора осуществляется поступающим на вход дешифратора двоичным кодом выбора номера дешифратора.

Для корректной индикации должно быть обеспечено синхронное выставление входного двоично-десятичного кода индицируемой цифры и кода номера индикатора. Т.е. в момент времени, когда на вход дешифратора подается двоичный код i -го номера подключаемого индикатора, на вход семисегментного преобразователя должен поступать двоично-десятичный код того же i -го разряда индицируемого десятичного числа. Отсюда следует, что динамическая индикация должна сопровождаться тактируемой схемой синхронизации и управления, что требует дополнительных аппаратных затрат. Поэтому динамическая индикация используется обычно совместно с устройствами, способными разделять во времени передачу по ограниченному набору линий двоично-десятичных кодов различных десятичных разрядов индицируемого числа. Наиболее часто динамическая индикация используется совместно с микропроцессорами и микроконтроллерами, где функция синхронизации реализуются программным путем.

Часто в цифровом устройстве, а особенно измерительном, приходится осуществлять обработку числовой информации со знаком. Такая информация обычно формируется двуполярным АЦП, способным оцифровывать как положительные, так и отрицательные амплитуды аналогового входного напряжения, и поступает из него в цифровое измерительное устройство для дальнейшей обработки. Поскольку знак может иметь только два значения – «+» или «-», то для отображения его бинарным кодом достаточно одного разряда. Для представления целых чисел фиксированной разрядности со знаком в двоичной системе счисления для отображения знака используется самый старший разряд. Для положительных чисел в старшем разряде записывается ноль, а для отрицательных – единица. Для выполнения арифметических операций над числами со знаком используются обычно дополнительные коды. В дополнительном коде старший разряд также имеет смысл не веса числа, а знака. Тем самым диапазон разрядной сетки цифрового устройства смещается симметрично относительно нуля. Например, при восьмиразрядном формате двоичные коды только положительных значений, когда старший разряд имеет смысл веса +128, будут представлены в диапазоне десятичных эквивалентов от 0 до +255. А при том же восьмиразрядном формате положительных и отрицательных значений, когда старший разряд имеет смысл знака, двоичные коды будут представлены в диапазоне десятичных чисел от –128 до +127. Смысл дополнительного кода заключается в том, что коды отрицательных значений, образованные весовыми разрядами модуля числа, должны быть дополнены до значения 2 ⁿ, где n - количество разрядов разрядной сетки цифрового устройства. Например, при восьмиразрядном формате дополнительный код числа –5 можно найти путем дополнения модуля числа 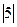до значения 2⁸=256. Т.е. дополнительный код числа –5 будет равен 251. Дополнительный же код положительных значений совпадает с прямым кодом их модулей с нулем в знаковом разряде. Часто дополнительный код отрицательных значений находят по следующему формальному правилу:

· инвертируются все весовые разряды модуля числа;

· прибавляется арифметически к полученному результату инвертирования единица;

· в старшем знаковом разряде в качестве признака отрицательного числа записывается единица.

Существует класс устройств, которые выполняют вышеуказанное преобразование и которые называются преобразователями в дополнительный код. Схема реализации такого преобразователя для пятиразрядного формата представлена на рис.8.35. Учитывая, что знаковый разряд определяет, будет ли выполняться инверсия входных разрядов и прибавление единицы, то, очевидно, что этот разряд должен быть управляющим для преобразователя. Если в нем ноль, то преобразование выполняться не будет и на выходе устройства должен присутствовать входной код без изменений. Если же в знаковом разряде будет единица, являющаяся признаком отрицательного числа, то преобразователь будет выполнять преобразование по указанному выше правилу. Отсюда следует, что в схеме преобразователя нужно применить управляемые инверторы. Такими элементами могут быть элементы «исключающее ИЛИ». При подаче знаковой единицы на один из входов элемента «исключающее ИЛИ», на его выходе будет формироваться инверсное значение переменной, подаваемой на второй вход. Для реализации суммирования с единицей в случае отрицательного числа можно использовать сумматор, на вход числа A которого подается код с выходов элементов «исключающее ИЛИ», а на самый младший разряд входа числа B – значение знакового разряда. Приведенная на рисунке схема будет выполнять преобразование в дополнительные коды чисел в диапазоне их десятичных эквивалентов от –16 до +15.

Если в результате операции над числами со знаком в знаковом разряде получается ноль, то результат является положительным и представлен в прямом коде. Если же в знаковом разряде результата окажется единица, то результат является отрицательным и представлен в дополнительном коде. Для перевода его в прямой код нужно воспользоваться преобразователем дополнительного кода в прямой. Правило преобразования дополнительных кодов отрицательных значений в прямые такое же, как и прямых в дополнительные. Т.е. схема преобразователя, реализующего обратное преобразование, будет точно такой же, как и показанная на рис. 8.35.

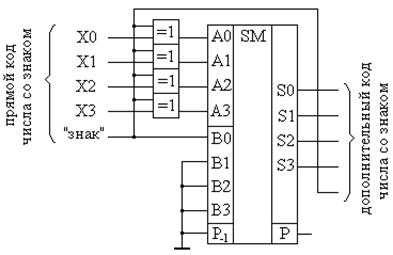
Рис.8.35. Схема преобразователя в дополнительный код для четырехразрядного числа с пятым знаковым разрядом.

Часто в измерительных цифровых устройствах возникает задача разработки датчика, кодирующего линейные или угловые перемещения. Подобные датчики часто строятся по принципу просвечивания маски, закрепленной на перемещающемся объекте, с нанесенными на нее прорезями и формирующими цифровой код, пропорциональный перемещению. Если с помощью такого датчика формировать обычный весовой двоичный код, то может возникнуть ситуация, когда соседние кодовые комбинации будут отличаться несколькими разрядами. Например, коды чисел 7 и 8 будут отличаться друг от друга четырьмя разрядами: 0111₂ и 1000₂. Это значительно повышает вероятность ошибки кодирования на границе перемещения из условной координаты 7 в условную координату 8. Эта ошибка может возникнуть по мере прохождения маски через граничный участок и смены нескольких разрядов одновременно из-за неидеальности и неточности изготовления как самой маски, так и считывателя кода с маски. В этом случае возможны ложные срабатывания и формирования промежуточных неверных кодов, которые могут быть восприняты обрабатывающим их цифровым устройством, что приведет к неверному результату. Для того, чтобы исключить такую возможность, на границах соседних координат должны формироваться коды, отличающиеся только одним разрядом. При этом последняя и первая координата также считаются соседними. Т.е. формируемый код должен быть невзвешенным. Примером такого кода является код Грея. Он идеально подходит для кодирования перемещения, поскольку позволяет получить минимальную погрешность кодирования, но имеет недостаток – сложность последующей обработки при выполнеии арифметических и логических операций. Поэтому код Грея используется только на начальной стадии кодирования пермещения в датчике, а в дальшей обработке его необходимо преобразовать в весовой двоичный код и использовать для его обработки стандартные правила и узлы устройств двоичной арифметики. Пордобное преобразование реализуется преобразовтелем кода Грея в двоичный. Для понимания принципа работы подобного преобразователя приведем пример формирования кода Грея для десятичных чисел в диапазоне от 0 до 15 (таблица 8.14).

Таблица 8.14.

Условная координата	Входы (код Грея)	Двоичные выходы
I3	I 2	I 1	I 0	X3	X2	X1	X0

Проделав описанные выше действия по нахождению МДНФ и выполнив ряд несложных тождественный преобразований, можно найти выражения для ФАЛ преобразователя кода Грея в весовой двоичный код:

.

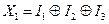
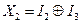
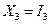Для обратного преобразования можно записать:

.

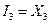Схема, реализующая преобразователь кода Грея в двоичный код, представлена на рис. 8.36.

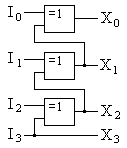
Рис. 8.36. Схема преобразователя кода Грея в двоичный код для чисел в диапазоне от 0 до 15.

Контрольные вопросы

1. Вычте из числа 57₁₀ число 83₁₀ и из числа 83₁₀ число 57₁₀ по правилам двоичной арифметики, используя дополнительные коды и операцию сложения.

2. Дайте определение функции алгебры-логики. Приведите различные формы записи для произвольной логической функции трех переменных.

3. Выполните минимизацию логической функции из предыдущего вопроса, используя диаграммы Вейча.

4. Как можно увеличить количество входов при использовании микросхем базовых логических элементов И-НЕ и ИЛИ-НЕ, количество входов которых недостаточно?

5. Что такое высокоимпедансное состояние?

6. В каких случаях целесообразно выбирать микросхемы с выходами, организованными по схеме с открытым коллектором?

7. Выполните синтез КЦУ в базисе И-НЕ для реализации ФАЛ четырех переменных, принимающую единичные значения на 1-м, 4-м, 7-м, 8-м, 10-м, 14-м и 15-м наборах.

8. Каковы преимущества и недостатки линейного и пирамидального дешифраторов?

9. Составьте таблицу истинности и структурную схему для четырехвходового шифратора.

10. Как реализовать схемы мультиплексора «из 8 в 1» и демультиплексора «из 1 в 8» на базе дешифратора?

11. Каким образом реализуются функции равенства, больше и меньше в цифровых компараторах?

12. Изобразите схему последовательного четырехразрядного двоичного сумматора, используя одноразрядные полные сумматоры с прямыми входами А и В, прямым входом переноса Р _-1 из предыдущего разряда и инверсным выходом переноса Р в старший разряд.

13. В чем заключается особенность построения параллельных сумматоров?

14. Изобразите схему перемножителя для двоичных чисел в диапазоне
-32…+31 их десятичных эквивалентов.

15. Какие виды кодов вам известны и по каким принципам строятся преобразователь для этих кодов?

16. В чем заключается особенность подключения индикаторов с объединенными и с разъединенными анодами к микросхемам семисегментных преобразователей?

Глава 9. Цифровые устройства последовательностного типа.

Дата добавления: 2015-05-09