Определения и основные свойства точечных оценок

Точечное оценивание параметров распределения.

Задача оценивания параметров распределения генеральной – одна из основных задач математической статистики. На содержательном уровне задача оценивания параметров распределения формулируется так: располагая выборкой реализаций случайной величины Х, необходимо получить оценку неизвестного параметра генеральной совокупности а и ее статистические свойства.

Оценивание параметров распределения осуществляется в два этапа. На первом этапе, на основании выборки х1, х2,...,, хn,строится статистика

,

значение которой при данной выборке х1, х2,...,, хn принимают за приближенное значение оцениваемого параметра а:

а .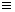

Так как параметр генеральной совокупности оценивается числом, которое на числовой оси изображается точкой, то оценку 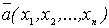называют точечной.

Для получения точечной оценки существует много статистик, которые могут быть использованы в качестве оценок. Поэтому второй этап оценивания состоит в выборе наилучшей оценки, что требует введения критерия качества получаемых оценок. Задача усложняется тем, что ввиду малого объема выборки требуется статистический подход к качеству оценки

По опытным данным (выборке) путем построения гистограммы или с помощью других средств можно попытаться выбрать вероятностную модель (определить закон распределения генеральной совокупности). При этом выборочные данные позволяют уточнить детали вероятностной модели. Знание вероятностной модели дает возможность прогнозировать будущие события, что важно для принятия решений. В приложениях обычно задаются определенным типом закона распределения генеральной совокупности (плотностью распределения)

f=f (x;a1,a2,...,am)

и по данным случайной выборки х1, х2,..., хn оценивают неизвестные параметры a1, a2,..., am. Чаще всего параметрами являются генеральное среднее и дисперсия, а качестве оценки тогда используют выборочные характеристики: выборочное среднее и выборочную дисперсию.

Рассмотрим следующую задачу. Пусть имеется случайная величина Х и нам известен ее закон распределения f = f (x, a), который содержит один неизвестный параметр а. Требуется на основании выборочных данных х1, х2,..., хn найти подходящую оценку параметра а. Для решения этой задачи построим следующую математическую модель. Пусть Х1, Х2,..., Хn – независимые случайные величины, которые принимают соответствующие выборочные значения (для данной выборки значения х1, х2,..., хn) и пусть случайная величина получена на основе случайных величин Х1, Х2,..., Хn, то есть 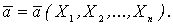Будем считать, как и ранее, что случайные величины Х1, Х2,..., Хn имеют один и тот же закон распределения с плотностью распределения величины Х (генеральной совокупности) f(x). Тогда является случайной величиной, закон распределения которой зависит от n и от f(x). Для того чтобы оценка имела практическую ценность она должна обладать следующими свойствами.

1. Несмещенность оценки. Оценка называется несмещенной, если ее математическое ожидание равно оцениваемому параметру генеральной совокупности:

В противном случае оценка называется смещенной и допускает систематическую ошибку. Так, рассмотренное ранее среднее выборочное 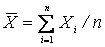является несмещенной оценкой среднего генерального. В то же время выборочная дисперсия - является смещенной оценкой генеральной дисперсии.

2. Состоятельность оценки. Оценка называется состоятельной, если она по вероятности с увеличением объема выборки п стремится к параметру генеральной совокупности:

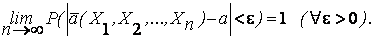
Это условие будет выполняться, если

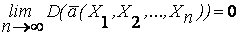
и оценка является несмещенной. Доказательство этого основано на неравенстве Чебышева.

3. Эффективность оценки. Если составлять множество несмещенных и состоятельных оценок, то эти оценки будут иметь разные дисперсии. Ясно, что, чем меньше будет дисперсия, тем меньше будет вероятность грубой ошибки при определении приближенного параметра генеральной совокупности. Поэтому нужно выбрать такую оценку, у которой дисперсия была бы минимальной:

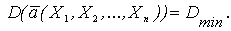
Такая оценка называется эффективной.

Заключение. При обработке экспериментальных данных необходимо руководствоваться сформулированными свойствами оценок.

В качестве примера покажем, что рассмотренные ранее оценки: выборочное среднее и выборочная дисперсия , будучи несмещенными, являются и состоятельными оценками. Действительно, так как согласно теореме Чебышева

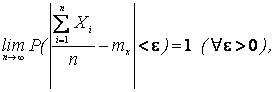
то выборочное среднее является состоятельной оценкой.

Для того чтобы доказать, что выборочная дисперсия является состоятельной оценкой, покажем вначале, что смещенная оценка - состоятельная оценка. С этой целью запишем:

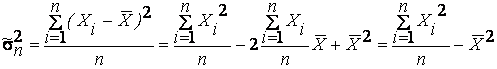(8.1)

При n ® ¥ по вероятности случайная величина стремится к М (Х2), а выборочное среднее – к среднему генеральному mx. Тогда из соотношения (1) следует, что по вероятности стремится при n ® ¥ к величине М (Х2)-mx2=D (X)=s2, которая является генеральной дисперсией. Тем самым доказана состоятельность оценки . Если теперь рассмотреть несмещенную оценку генеральной дисперсии 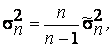то поскольку множитель стремится к единице при n ® ¥, а стремится по вероятности к , то и оценка 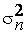стремится по вероятности к , что доказывает состоятельность оценки .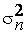

Замечание. Для простоты изложения формулы оценок математического ожидания и дисперсии, которые были использованы при доказательстве свойств оценок, были построены с использованием статистического ряда. Если данные выборки представлено в виде интервального вариационного ряда, то для вычисления соответствующих выборочных числовых характеристик используют следующие формулы.

1. Выборочное взвешенное среднее :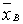

.

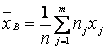2. Выборочная взвешенная дисперсия :

,

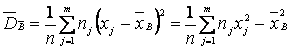которая является смещенной оценкой и несмещенная оценка

.

Здесь п – объем выборки, т – число разных вариант, nj – частоты вариант (п1+п2+…+пт=п).

16. Интервальное оценивание параметров распределения. Интервальное оценивание генерального среднего нормального распределения.

Пусть во выборке для параметра θ найдена точечная оценка θ^*. Обычно исследователи заранее задаются некоторой достаточно большой вероятностью γ (например, 0,95; 0,99 или 0,999) такой, что событие с вероятностью γ можно считать практически достоверным, и ставят вопрос об отыскании такого значения ε > 0, для которого
.
Видоизменив это равенство, получим:

и будем в этом случае говорить, что интервал ]θ^*–ε; θ^*+ε[ покрывает оцениваемый параметр θ с вероятностью γ.
Интервал ]θ^*–ε θ^*+ε[ называется доверительным интервалом.
Вероятность γ называется надежностьюили доверительной вероятностью интервальной оценки.
Концы доверительного интервала, т.е. точки θ^*–ε и θ^*+ε называются доверительными границами.
Число ε называется точностью оценки.
В качестве примера задачи об определении доверительных границ, рассмотрим вопрос об оценке математического ожидания случайной величины Х, имеющей нормальный закон распределения с параметрами а и σ, т.е. Х = N (a,σ). Математическое ожидание в этом случае равно а. По наблюдениям x ₁, x ₂, …, x_n вычислим среднее и оценку дисперсии σ².
Оказывается, что по данным выборки можно построить случайную величину , которая имеет распределение Стьюдента (или t -распределение) с ν= n –1 степенями свободы.
Воспользуемся таблицей П.3 и найдем для заданных вероятности γ и числа n число t _γ такое, при котором вероятность
P(| Т | < t _γ) = γ, или
.
Сделав очевидные преобразования, получим

Итак, пользуясь распределением Стьюдента, мы нашли доверительный интервал 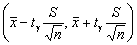, покрывающий неизвестный параметр а с надежностью γ. Здесь случайные величины и S заменены неслучайными величинами и s, найденными по выборке. По таблице П.3, по заданным n и γ можно найти t _γ.
Графическая иллюстрация схемы нахождения точности ε и доверительных границ, отвечающих надежности γ приведена на рис. 5.1. Доверительная вероятность γ будет соответствовать площади под кривой Стьюдента, заключенной между точками – t _γ и t _γ.




Рис. 3.1

Замечание. При n => ∞ распределение Стьюдента стремится к нормальному распределению. Поэтому при больших n (практически при n ≥ 30) t _γ можно получить по таблице П.2 из уравнения Ф(t _γ) = γ/2.
Для оценки среднего квадратического отклонения s нормально распределенного количественного признака Х с надежностью g по исправленному выборочному среднему квадратическому отклонению s служат доверительные интервалы:
s (1 – q) < s < s (1 + q) при q <1,
0 < s < s (1 + q) при q >1,
где q находят по таблице П. 4 по заданным n и γ.
Задача 3.1. Найти доверительные интервалы для оценки математического ожидания а и среднего квадратического отклонения s выручки магазина по результатам вычислений из 3.4. Надежность γ = 0,95.
Решение. Ниже будет показано, что распределение выручки магазина является нормальным. В 4.4 были получены следующие точечные оценки а ≈ = 30,77 тыс. руб.,
(тыс. руб)², где n =90 – объем выборки. Следовательно, σ≈s=6,83 тыс.руб.
По таблице П.1.2 при γ/2 =0,475 находим t _γ= 1,96. Вычисляем точность оценки , доверительные границы . Получаем доверительный интервал 29,4< a < 32,2.
Находим доверительный интервал для оценки σ. По таблице П.4 при γ = 0,95 и n = 90 получаем q = 0,151. Вычисляем доверительные границы s (1 – q)=6,83∙0,849 ≈ 5,8 и s (1+ q) = 6,83∙1,151 ≈ 7,9. Получаем доверительный интервал 5,8 < σ < 7,9.

Доверительный интервал для оценки математического ожидания при известном .

Пусть количественный признак генеральной совокупности распределен нормально. Известно среднее квадратическое отклонение этого распределения-. Требуется оценить математическое ожидание а по выборочной средней. Найдем доверительный интервал, покрывающий а с надежностью .Выборочную среднюю будем рассматривать как случайную величину (она изменяется от выборки к выборке), выборочные значения признака- как одинаково распределенные независимые СВ с математическим ожиданием каждой а и средним квадратическим отклонением . Примем без доказательства, что если величина Х распределена нормально, то и выборочная средняя тоже распределена нормально с параметрами

.

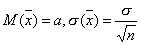Потребуем, чтобы выполнялось равенство

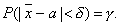
Заменив Х и , получим

получим

Задача решена. Число t находят по таблице функции Лапласа Ф(х).

Пример1. СВХ распределена нормально и  =3. Найти доверительный интервал для оценки математического ожидания по выборочным средним, еслиn = 36 и задана надежность  =0,95.

Из соотношения 2Ф(t)= 0,95, откуда Ф(t) = 0,475 по таблице найдем t: t =1,96. Точность оценки

Доверительный интервал

.

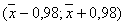Пример2. Найти минимальный объем выборки, который обеспечивает заданную точность  =0,3 и надежность  = 0,975, если СВХ распределена нормально и  =1,2.

Из равенства

выразим n:

,

подставим значения и получим минимльный объем выборки n ~ 81.

Дата добавления: 2015-05-09