Тренировочные задачи

Общая схема исследования функции и построения графиков

Асимптоты функции

Следующей дополнительной характеристикой функции 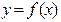являются асимптоты. Это - прямые, к которым стремится график функции при неограниченном возрастании (или убывании) аргумента. Существуют три вида асимптот, которые поясним чертежом:

Приведем, без доказательств, технику определения асимптот:

· Вертикальные асимптоты х=а находятся из анализа области определения функции . Например, у = 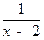не определена в точке х=2, следовательно, х=2 и есть вертикальная асимптота.

· Если существует предел или 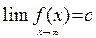(или оба вместе), то уравнения у= b или (и) у=с определяют горизонтальныеасимптоты.

· Если существуют конечные пределы 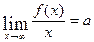и 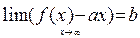, причем оба одновременно, то прямая у=аx+b является наклонной асимптотой графика функции .

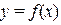В современных условиях построение графиков осуществляется на практике, как правило, по точкам или с помощью компьютера. Однако в задачах с повышенной ответственностью необходимо использовать описанные выше приемы. Полная последовательность анализа функции и построения ее графика состоит из следующих этапов:

· Находится область определения функции 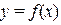и вертикальные асимптоты, если они есть.

· Устанавливается тип функции: четная, нечетная, общего вида.

· Из решения уравнения определяются корни функции, т.е. точки ее пересечения с осью оХ.

· Вычисляются производные и .

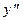· Определяются экстремумы функции.

· Определяются точки перегиба и исследуются выпуклости функции.

· Проверяется наличие горизонтальных и наклонных асимптот.

· При необходимости детализации, вычисляются значения функции в нескольких дополнительных точках.

· Все полученные результаты отображаются на плоскости, и строится график.

Расчеты и отображение результатов обычно делаются одновременно. Этапы 2, 6 и 7, во многих случаях, можно опустить.

Примеры решения задач

Наиболее часто встречающимися применениями дифференцирования на практике являются раскрытие неопределенных пределов (правило Лопиталя) и исследование особенностей изменяемости функций, в том числе построение графиков функций. Приведем типовые примеры по теме.

1. Вычислить

Решение: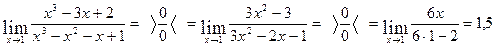

Ответ: 1,5.

2. Вычислить

Решение: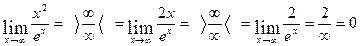

Ответ: функция – бесконечно малая при .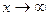

3. Вычислить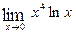

. Для раскрытия неопределенности такого типа следует предварительно преобразовать произведение в дробь.

Возможны два варианта:

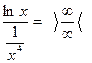или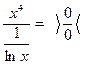

Только после этого можно применить правило Лопиталя. Используя первый вариант, получим:

.

Ответ: функция – бесконечно малая при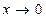

4. Вычислить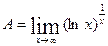

Здесь имеет место случай 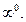Для раскрытия таких пределов удобно сначала прологарифмировать заданную функцию и затем применить правило Лопиталя. Имеем:

.

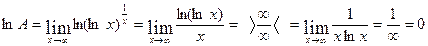Так как ln A = 0, то А = е ⁰ = 1.

Ответ: 1.

5. Найти экстремумы функции у =(1 – х ²)³.

Найдем производную: Стационарные точки: 6 х (1 – х ²)²=0, откуда х ₁=0; х ₂= –1; х ₃=1. Используем первое достаточное условие экстремума:

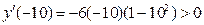
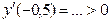
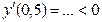
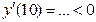
Для определения знака производной внутри интервалов проще всего выбрать произвольные удобные для вычислений точки, что и показано на схеме.

Таким образом, заданная функция имеет один максимум в точке х = 0, возрастает при x < 0 и убывает при х > 0. Максимальное значение функции у _max = f (0) = (1 – 0²)³=1.

Ответ: у _max=1.

6. Найти экстремумы функции .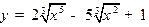

Дифференцируем:. Производная, очевидно, не существует при х =0. Кроме того, она равна 0 при х =1. Следовательно, имеем две стационарные точки х ₁=0 и х ₂=1. Опять используем первое достаточное условие:

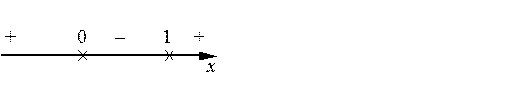
Здесь для определения знаков производной в интервалах вычислялись: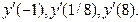

Таким образом, заданная функция имеет максимум при х =0 и минимум при х =1. Соответствующие экстремальные значения: у _max= f (0)=...=1, y _min= f (1)=...= –2.

Ответ: у _max=1, y _min= –2.

7. Найти экстремумы функции у = 3 – 2 х ² + х ⁴

Дифференцируем: .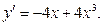

Стационарные точки: 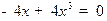, откуда ; .

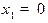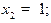
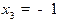Используем второе достаточное условие. Вторая производная: 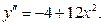. Таким образом:

,

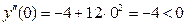т.е. 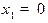является точкой максимума и

,

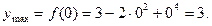
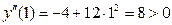т.е. является точкой минимума и

.

,

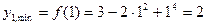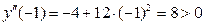т.е. 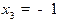является второй точкой минимума и

.

8. Исследовать выпуклости функции у =3 х ⁴ – 4 х ³.

Дифференцируем: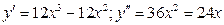

Стационарные значения для второй производной: 36 х ² – 24 х =0, откуда х ₁=0 и х ₂=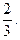

Вычисляя знаки второй производной в интервалах обычным образом, заключаем, что обе точки будут точками перегибов заданной функции, причем при х < 0 и х > функция вогнутая, а при 0 < x < функция выпуклая.

Ординаты точек перегиба:

9. Исследовать функцию 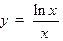и построить ее график.

· ОДЗ этой функции: x >0. Вертикальная асимптота: х =0.

· Уже по ОДЗ ясно, что заданная функция – общего вида.

· Определим точку пересечения с осью оХ: , откуда 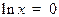и х = 1.

· Дифференцируем: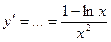

· Определим стационарные точки. Значение х =0 исключаем, как не вошедшее в ОДЗ. Тогда: 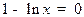, откуда х = е.

· Выберем второе достаточное условие.

Вторая производная: .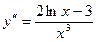

Тогда, т.е. точка х = е является точкой максимума и 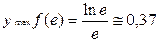. Заданная функция возрастает при x < e и убывает при x > e.

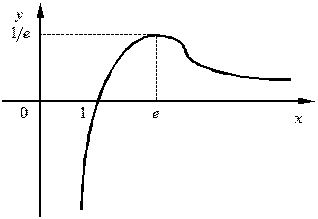
· Определим выпуклости заданной функции.Стационарные значения второй производной , откуда х = е ^1,5. Таким образом, точка х = е ^1,5 является точкой перегиба, причем слева от нее функция выпукла, а справа – вогнута. Ордината у _пер.=...= .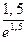

· Проверим горизонтальную асимптоту:

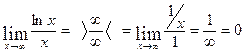, следовательно, ось оХ является горизонтальной асимптотой.

Вопросы для самоконтроля:

1. Правило Лопиталя.

2. Возрастание и убывание функций.

3. Необходимое условие экстремума.

4. Первое достаточное условие экстремума.

5. Второе достаточное условие экстремума.

6. Глобальные экстремумы.

7. Выпуклость и вогнутость функции.

8. Асимптоты.

9. Общая схема исследования функции и построение графиков.

Вычислить пределы с помощью правила Лопиталя:

1.

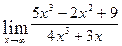
Ответ: 1,25

2.

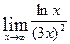
Ответ: 0

3. Определить экстремумы функции у =4 х ³ +3 х ² – 2 х + 8.

Ответ: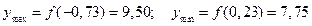

4. Определить выпуклости функции .

5. Построить график функции 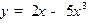с применением производной.

Дата добавления: 2015-05-10